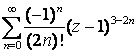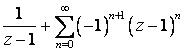- •Тема 5. Теория функции комплексного переменного. Производная и интеграл. Условия Коши-Римана
- •5.1. В каких точках заданная функция является дифференцируемой?
- •5.2. В каких точках заданная функция является аналитической?
- •5.3. Найти интеграл от заданной функции по заданному контуру. Обход
- •5.4. Определение особых точек
- •5.5. Нахождение вычетов
- •5.6. Вычисление интегралов с помощью вычетов.
- •5.7. Разложение функции в ряды Тейлора и Лорана
- •5.8 Комплексные числа.
- •5.9. Теория
- •Тема 6. Операционное исчисление
- •6.1. Нахождение изображений и оригиналов
- •6.2. Дифференциальные уравнения.
- •6.3. Теория
6.2. Дифференциальные уравнения.
6.2.1.Решением задачи Коши
![]() является функция
является функция
#2)
![]() ;
;
6.2.2. Решением задачи Коши
![]() является функция
является функция
1)#![]() ;
;
6.2.3.Решением задачи Коши
![]() является функция
является функция
#2)![]() ;
;
6.2.4. Решением задачи Коши
![]() является функция
является функция
#4)![]() ;
;
6.2.5. Решением задачи Коши
![]() является функция
является функция
#2)![]() ;
;
6.2.6. Решением задачи Коши
![]() является функция
является функция
#5)
![]()
6.2.7. Решением дифференциального
уравнения
![]() в области изображений является
в области изображений является
#1)
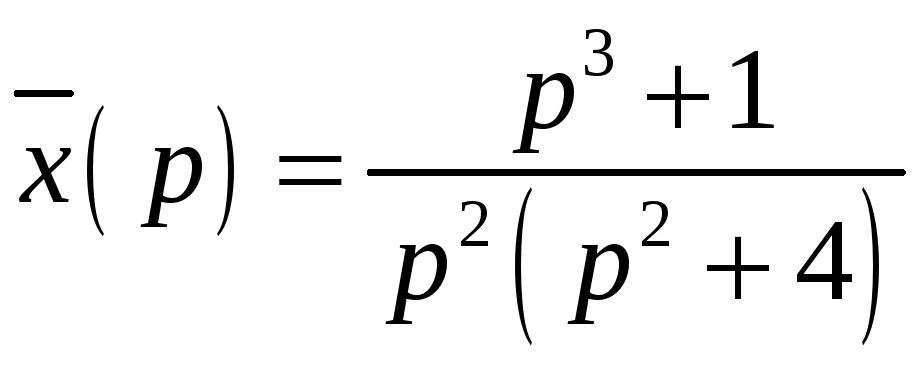
6.2.8. Решением дифференциального
уравнения
![]() в области изображений является
в области изображений является
#3)
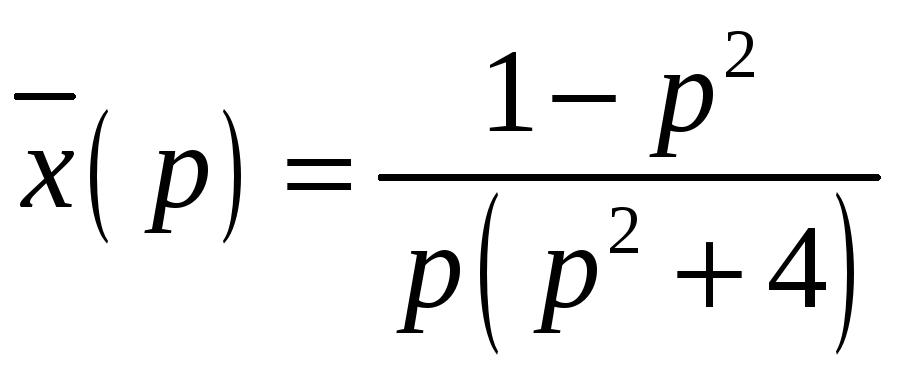
6.2.9. Решением дифференциального
уравнения
![]() в области изображений является
в области изображений является
#2)
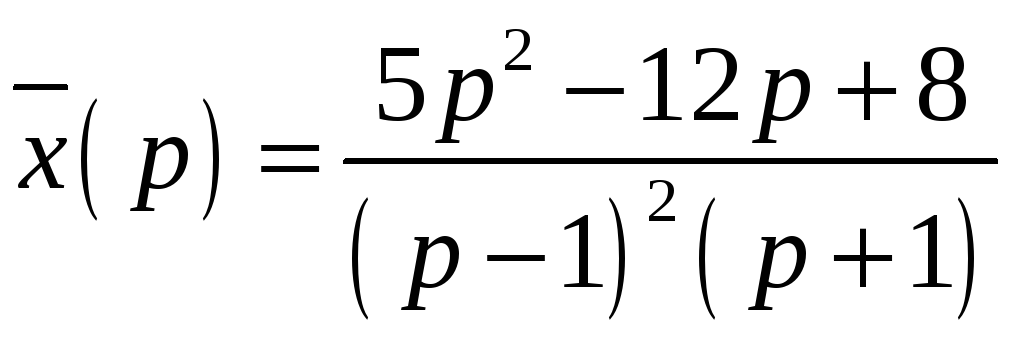
6.2.10. Решением дифференциального
уравнения
![]() в области изображений является
в области изображений является
#5)
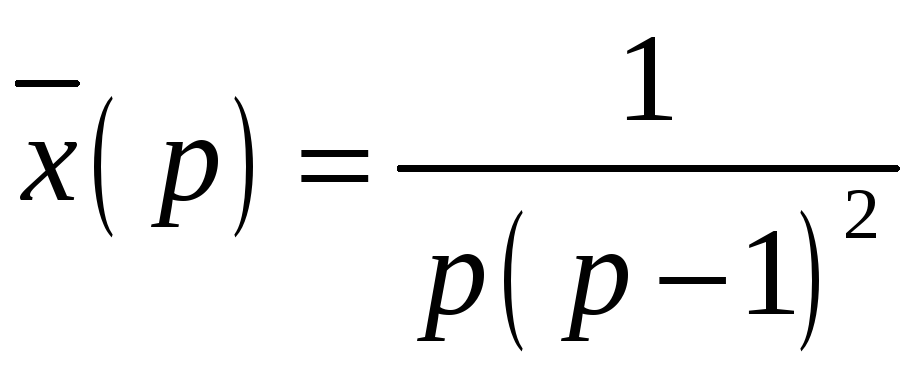
6.3. Теория
6.3.1. Изображением функции
![]() называют функцию
называют функцию
![]() ,
определяемую формулой
,
определяемую формулой
#2)
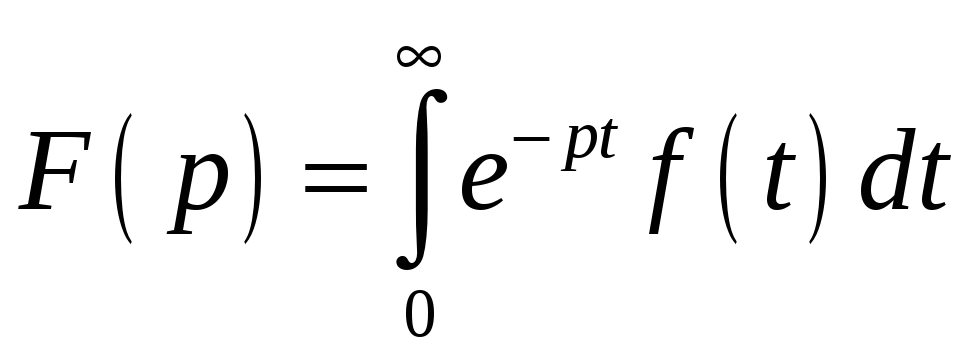
6.3.2. Если функция
![]() имеет изображение
имеет изображение
![]() ,
,
![]() ,
то
,
то
#5)
![]()
6.3.3. Если функция
![]() имеет изображение
имеет изображение
![]() ,
,
![]() ,
то
,
то
#1)
![]()
6.3.4. Если
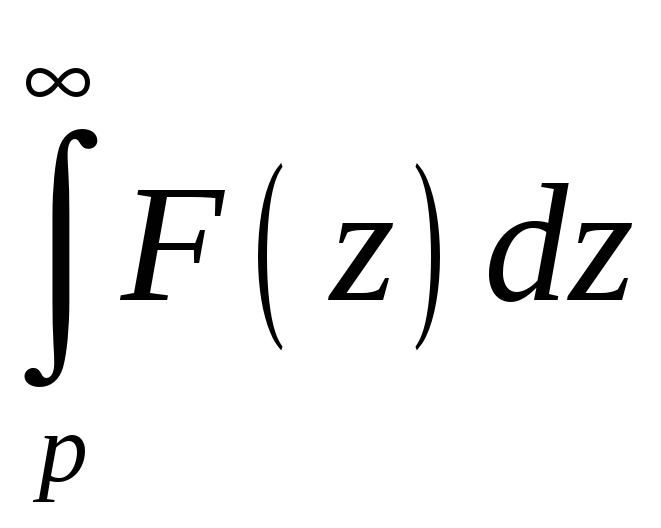 сходится, то он является изображением
функции
сходится, то он является изображением
функции
#4)
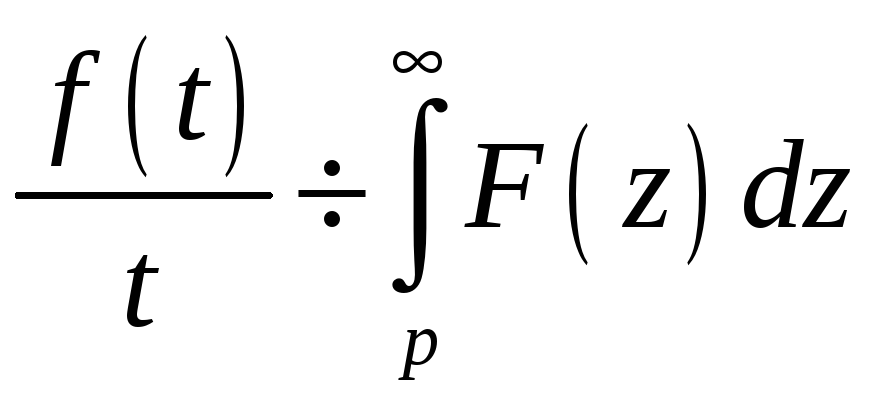
6.3.5. Если функция
![]() имеет изображение
имеет изображение
![]() ,
,
![]() ,
то
,
то
#3)
![]()
6.3.6. Теорема смещения формулируется следующим образом:
#4) Если
![]() есть изображение функции
есть изображение функции
![]() ,
то
,
то
![]() есть
изображение функции
есть
изображение функции
![]() .
.
6.3.7. Теорема о свёртывании утверждает, что
#4)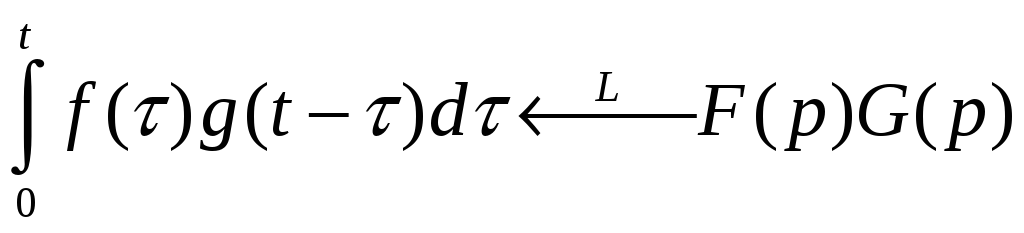 ;
;
6.3.8. Свойство линейности преобразования Лапласа
формулируется следующим образом:
#2)![]() ;
;
6.3.9. Теорема подобия утверждает, что
#2)![]() ;
;
6.3.10. Из теоремы о дифференцировании оригинала следует, что
#3)![]() ;
;
6.3.11. Из теоремы о дифференцировании изображения следует, что
#2)![]() ;
;
6.3.12. Теорема запаздывания утверждает, что
# 5)![]() .
.
-
Если функция
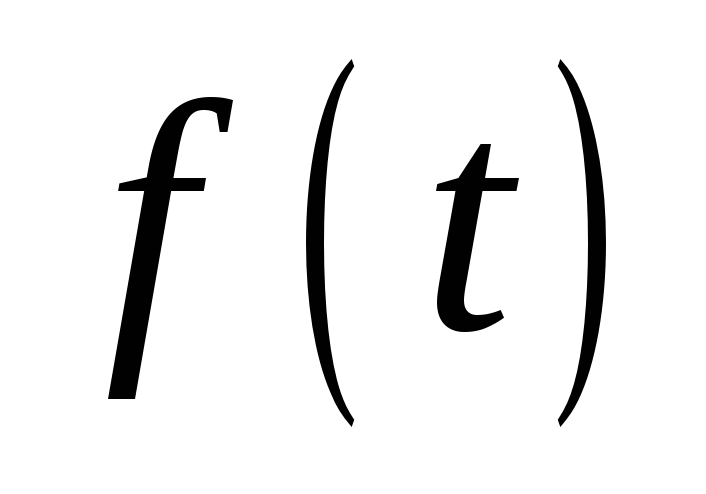 имеет изображение
имеет изображение
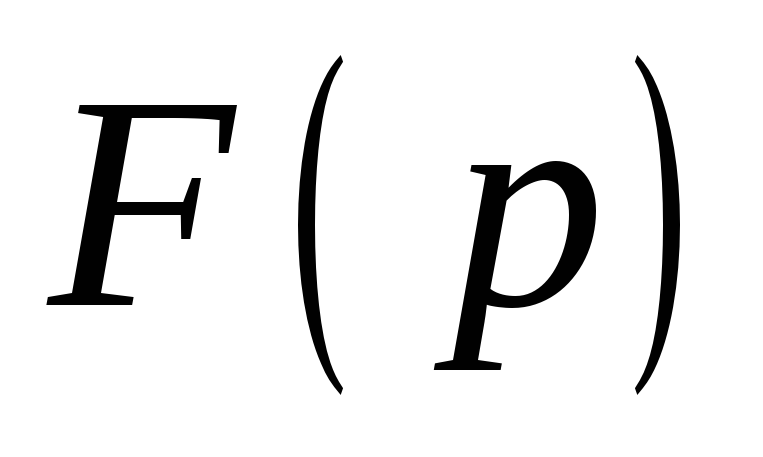 ,
,
 ,
то
,
то
#1)
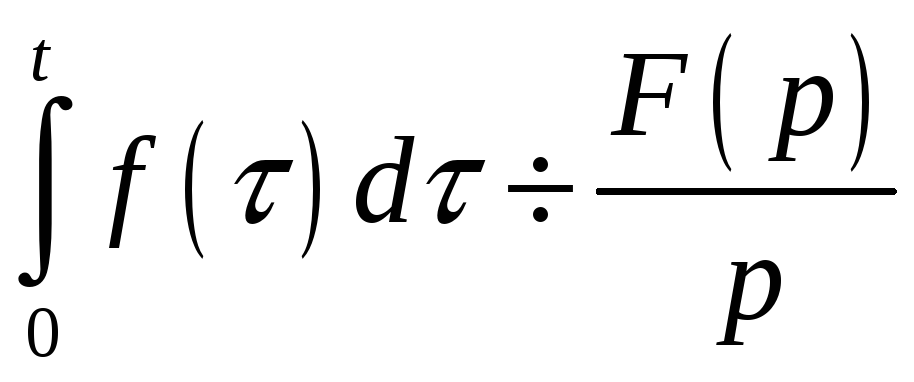
В
каких точках заданная функция является
дифференцируемой?
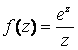
![]() в
каждой комплексной точке
в
каждой комплексной точке
В
каких точках заданная функция является
аналитической?
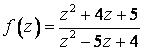
![]() всюду,
кроме точек
всюду,
кроме точек
![]() и
и
![]()
В
каких точках заданная функция является
аналитической?
![]()
![]() всюду,
кроме точек
всюду,
кроме точек
![]() и
и
![]()
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() всюду,
кроме точки
всюду,
кроме точки
![]()
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() лишь
в точке
лишь
в точке
![]()
В
каких точках заданная функция является
аналитической?
![]()
![]() ни
в одной точке
ни
в одной точке
В
каких точках заданная функция является
аналитической?
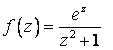
![]() всюду,
кроме точек
всюду,
кроме точек
![]() и
и
![]()
В каких точках
заданная функция является аналитической?
![]()
-
 ни
в одной точке
ни
в одной точке
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() лишь
в точке
лишь
в точке
![]()
В
каких точках заданная функция является
аналитической?
![]()
![]() ни
в одной точке
ни
в одной точке
В
каких точках заданная функция является
аналитической?
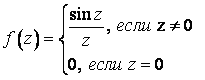
![]() всюду,
кроме точки
всюду,
кроме точки
![]()
В
каких точках заданная функция является
аналитической?
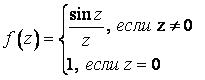
![]() в
каждой комплексной точке
в
каждой комплексной точке
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() в
каждой комплексной точке
в
каждой комплексной точке
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() ни
в одной точке
ни
в одной точке
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() в
каждой комплексной точке
в
каждой комплексной точке
В
каких точках заданная функция является
аналитической?
![]()
![]() в
каждой комплексной точке z
в
каждой комплексной точке z
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() на
мнимой оси
на
мнимой оси
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() ни
в одной точке
ни
в одной точке
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() всюду,
кроме точки
всюду,
кроме точки
![]()
В
каких точках заданная функция является
дифференцируемой?
![]()
![]() на
мнимой оси
на
мнимой оси
Изображением
функции
![]() является
функция
является
функция
![]()
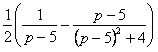
Изображением
функции
![]() является
функция
является
функция
![]()
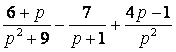
Изображением
функции
![]() является
функция
является
функция
![]()
![]()
Изображением
функции
 является
функция
является
функция
![]()
![]()
Используя
определение преобразования Лапласа
или теорему запаздывания, найдите
изображение функции
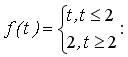
![]()
![]()
Из теоремы о дифференцировании изображения следует, что
![]()
![]()
Из теоремы о дифференцировании оригинала следует, что
![]()
![]()
Изображением
функции
![]() является
функция
является
функция
![]()
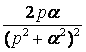
Изображением
функции
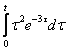 является
функция
является
функция
Используя
определение преобразования Лапласа,
найдите изображение функции
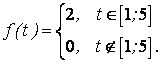
![]()
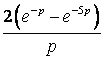
Используя
определение преобразования Лапласа,
найдите изображение функции
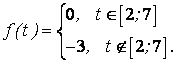
![]()
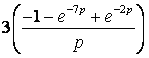
Найти
вычет функции
![]() в
точке
в
точке
![]()
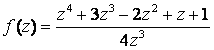
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
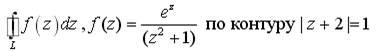
![]() 0
0
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
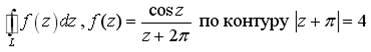
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
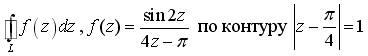
![]()
![]()
Найти
![]() для
заданной функции,
для
заданной функции,
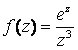
Найти
![]() для
заданной функции,
для
заданной функции,
![]()
![]()
![]()
Найти
вычет функции
![]() в
точке
в
точке
![]() ,
,
![]()
![]()
![]()
Найти
вычет функции
![]() в
точке
в
точке
![]() ,
,
![]()
![]()
![]()
Найти
вычет функции
![]() в
точке
в
точке
![]() ,
,
![]()
![]() 2
2
Найти вычет функции
![]() в
точке
в
точке
![]()

Найти
вычет функции
![]() в
точке
в
точке
![]() ,
,
![]()
![]() 1
1
Найти
![]() для
заданной функции,
для
заданной функции,
![]()
![]() 0
0
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
![]()
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
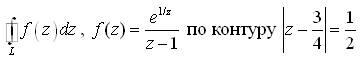
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
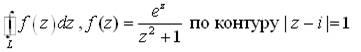
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
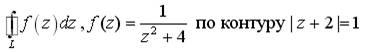
![]() 0
0
Найти
![]() для
заданной функции,
для
заданной функции,
![]()
![]()
![]()
Найти
![]() для
заданной функции,
для
заданной функции,
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
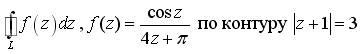
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
![]()
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
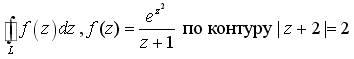
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
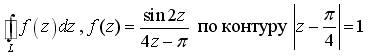
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
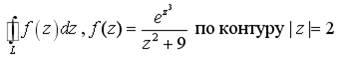
![]() 0
0
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
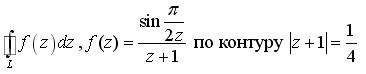
![]()
![]()
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
![]()
![]()
![]()
Найти интеграл от
заданной функции по заданному контуру.
Обход осуществляется против часовой
стрелки.
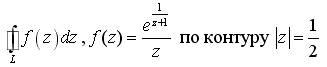
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
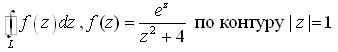
![]() 0
0
Найти
интеграл от заданной функции по заданному
контуру. Обход осуществляется против
часовой стрелки.
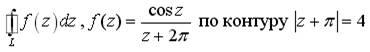
![]()
![]()
Определить
характер особой точки и саму особую
точку для заданной функции
![]()
![]()
![]() –
существенно особая
точка
–
существенно особая
точка
Определить
характер особой точки и саму особую
точку для заданной функции
![]()
![]()
![]() –
правильная точка
–
правильная точка
Определить
характер особой точки и саму особую
точку для заданной функции
![]()
![]()
![]() –
правильная точка
–
правильная точка
Определить
характер особой точки и саму особую
точку для заданной функции
![]()
![]()
![]() –
существенно особая
точка
–
существенно особая
точка
Определить
характер особой точки и саму особую
точку для заданной функции
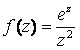
![]() в
точке
в
точке
![]() полюс
второго порядка
полюс
второго порядка
Определить
характер особой точки и саму особую
точку для заданной функции
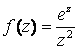
![]() в
точке
в
точке
![]() полюс
второго порядка
полюс
второго порядка
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
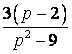 является
функция
является
функция
![]()
![]()
Оригиналом функции
![]() является
функция
является
функция
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция вида
является
функция вида
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
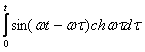
Оригиналом функции
![]() является
функция
является
функция
Оригиналом
функции
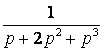 является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
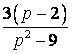 является
функция
является
функция
![]()
![]()
Оригиналом
функции
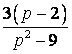 является
функция
является
функция
![]()
![]()
Оригиналом функции
![]() является
функция
является
функция
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом функции
![]() является
функция
является
функция
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Оригиналом
функции
![]() является
функция
является
функция
![]()
![]()
Пусть
![]() .
Тогда изображением функции
.
Тогда изображением функции
![]() является
функция
является
функция
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
![]()
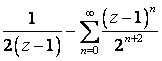
Разложить в ряд
Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
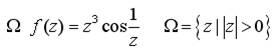
Разложить
в ряд Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
![]()
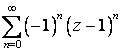
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
![]()
![]()
![]()
Разложить в ряд
Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
![]()
Разложить в ряд
Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
![]()
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
![]()
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
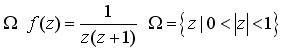
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
![]()
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
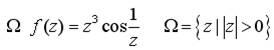
![]()
![]()
Разложить в ряд
Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
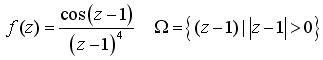
![]()

Разложить
в ряд Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
![]()
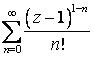
Разложить
в ряд Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
![]()
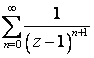
Разложить
в ряд Лорана указанную функцию
![]() по
степеням
по
степеням
![]() в
заданной области
в
заданной области
![]()
![]()
![]()
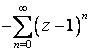
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
![]()
![]()
![]()
Разложить
в ряд Лорана указанную функцию
![]() по
степеням z в заданной области
по
степеням z в заданной области
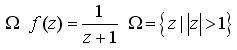
![]()
![]()
С
использованием теоремы об умножении
(находя изображение и затем оригинал)
вычислите свёртку
![]() :
:
![]()
![]()
Свойство линейности преобразования Лапласа формулируется следующим образом:
![]()
![]()
Свёртка
![]() определяется
как интеграл
определяется
как интеграл
![]()
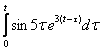
Теорема запаздывания утверждает, что
![]()
![]()
Теорема о свёртывании утверждает, что
![]()
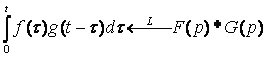
|
|
|
|
|
|
|
Теорема подобия утверждает, что
![]()
![]()
Теорема смещения формулируется следующим образом:
![]() Если
Если
![]() есть
изображение функции
есть
изображение функции
![]() ,
то
,
то
![]() есть
изображение функции
есть
изображение функции
![]()