5.8 Комплексные числа.
5.8.1. Определите модуль
и аргумент
комплексного числа
.
#2)
.
5.8.2. Определите модуль
и аргумент
комплексного числа
.
#3)
.
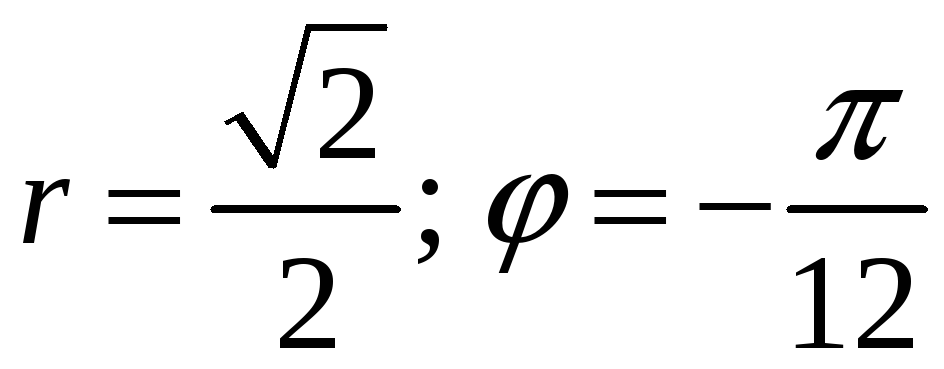5.8.3. Определите модуль
и аргумент
комплексного числа
.
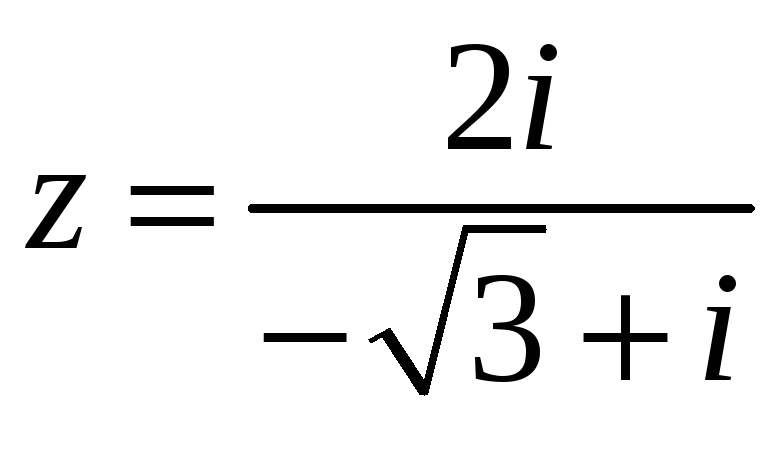#5)
.
5.8.4. Определите модуль
и аргумент
комплексного числа
.
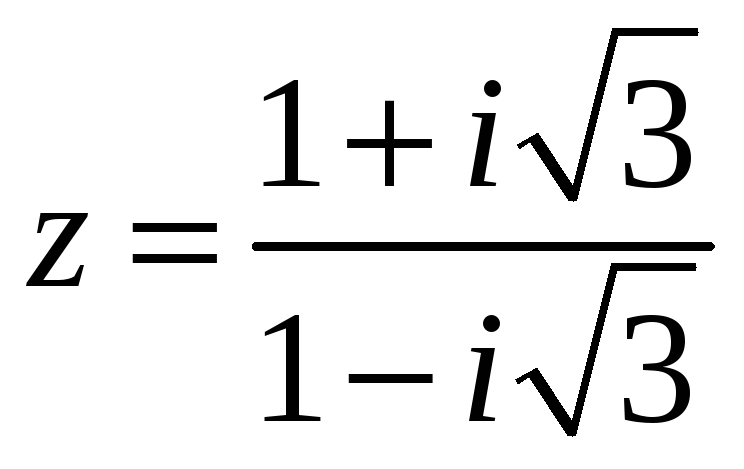#2)
.
5.8.5. Определите модуль
и аргумент
комплексного числа
.
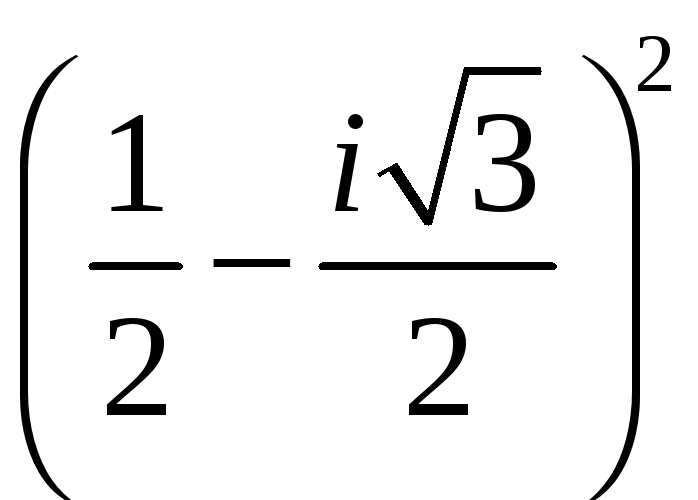#5)
.
5.8.6. Определите модуль
и аргумент
комплексного числа
.
#4)
.
5.8.7. Определите модуль
и аргумент
комплексного числа
.
#2)
.
5.8.8. Определите модуль
и аргумент
комплексного числа
.
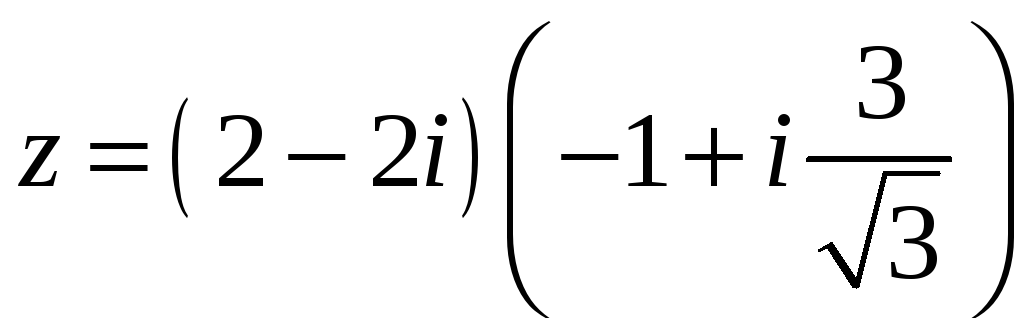#3)
.
5.8.9. Определите модуль
и аргумент
комплексного числа
.
#1)
.
5.8.10. Вычислите определитель
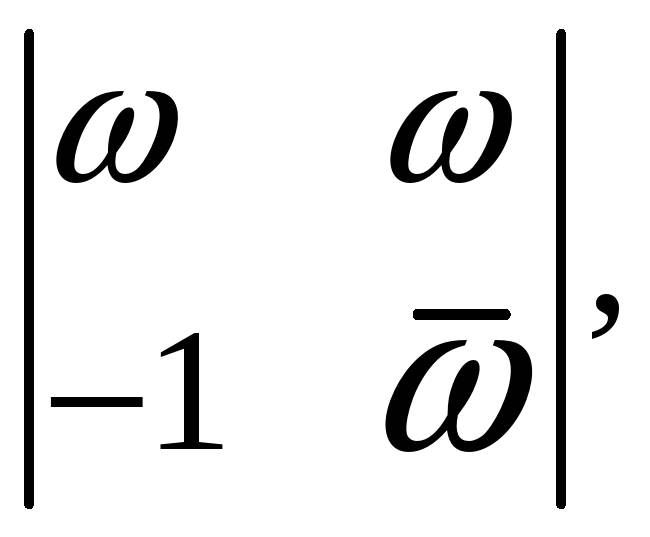где
.
#1)
.
5.8.11. Вычислите определитель
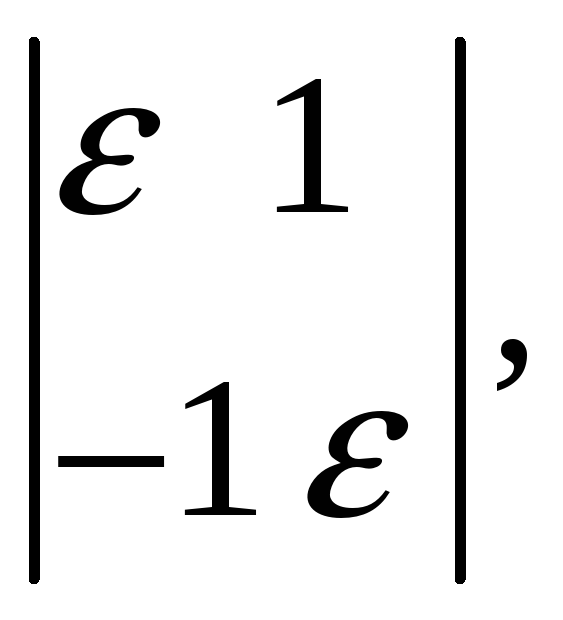где
.
#4)
.
5.8.12. Вычислите определитель
где
.
#5)
.
5.8.13. Вычислите определитель
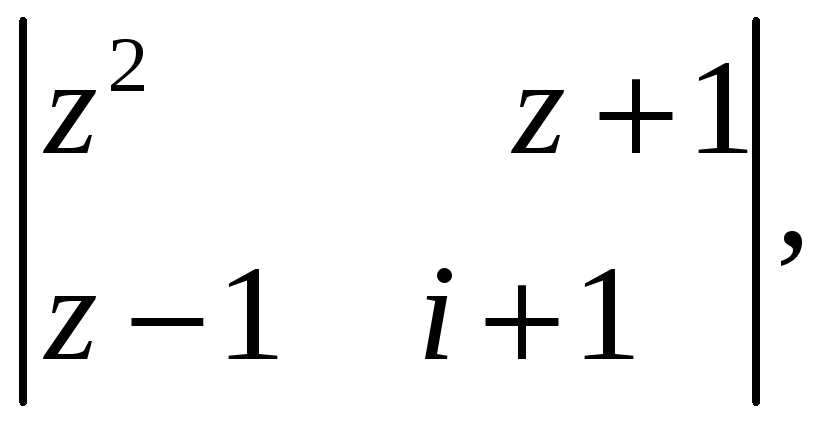где
.
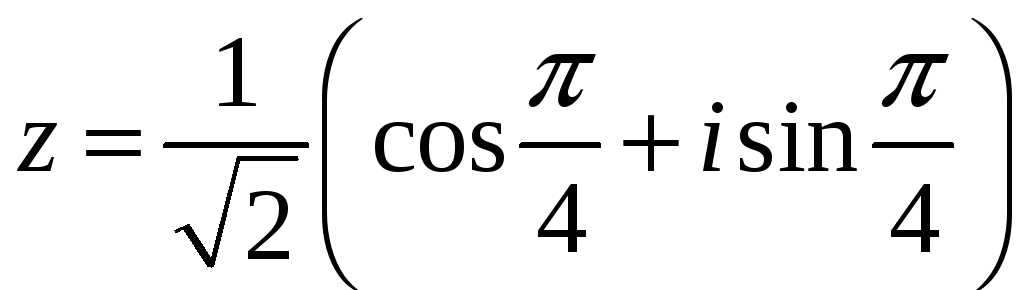#1)
.
5.8.14. Вычислите определитель
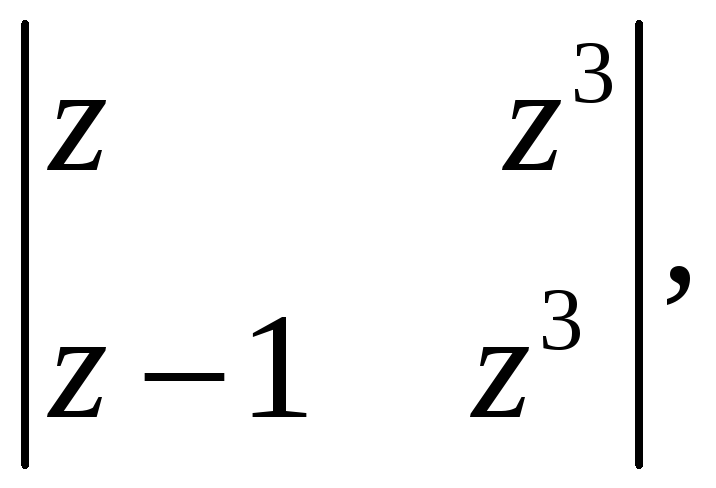где
.
#2)
.
5.8.15. Вычислите определитель
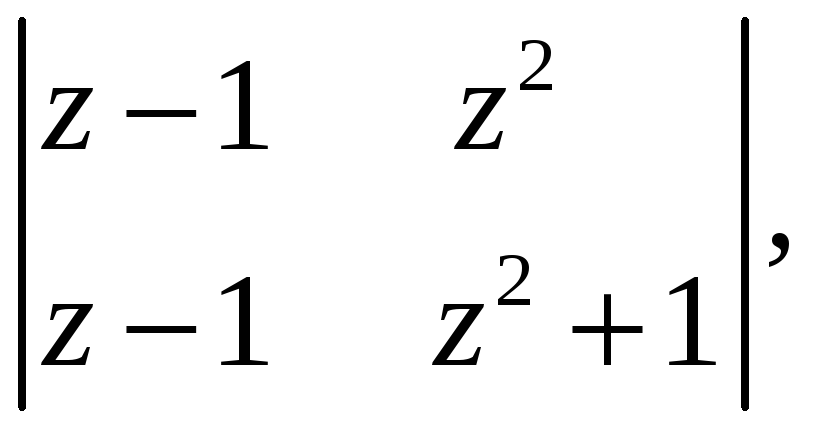где
.
#3)
.
5.8.16. Вычислите действительную
и мнимую
части
комплексного числа
.
#1)
.
5.8.17. Вычислите действительную
и мнимую
части
комплексного числа
.
#3)
.
5.8.18. Вычислите действительную
и мнимую
части
комплексного числа
.
#5)
.
5.8.19. Вычислите действительную
и мнимую
части
комплексного числа
.
#4)
.
5.8.20. Вычислите действительную
и мнимую
части
комплексного числа
.
#2)
.
5.8.21. Вычислите действительную
и мнимую
части
комплексного числа
.
#5)
.
5.8.22. Определите все комплексные
решения уравнения
.
#1)
.
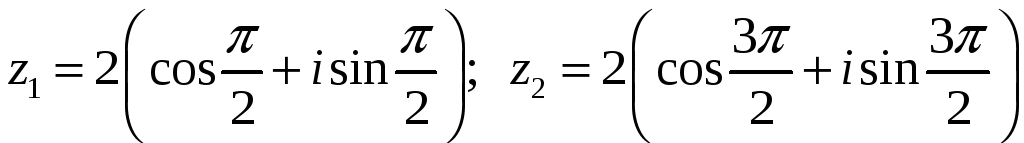5) Уравнение решений не имеет.
5.8.23. Определите все комплексные
решения уравнения
.
#5)
.
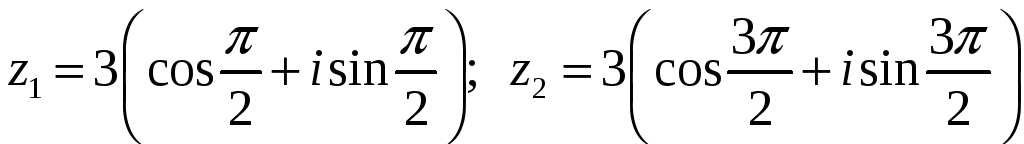5.8.24. Определите все комплексные
решения уравнения
.
#2)
.
5.8.25. Определите все комплексные
решения уравнения
.
#3)
.
5.8.26. Определите все комплексные
решения уравнения
.
#5)
.
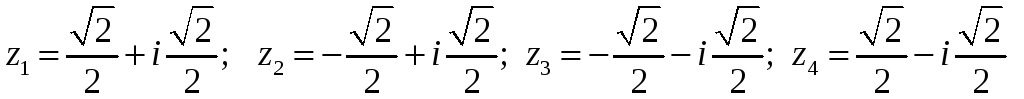5.8.27. Определите все комплексные
решения уравнения
.
#2)
5.8.28. Вычислить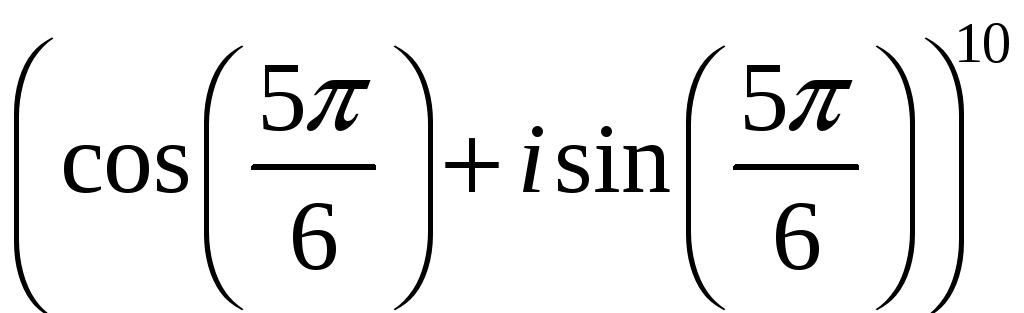
.
#2)
.
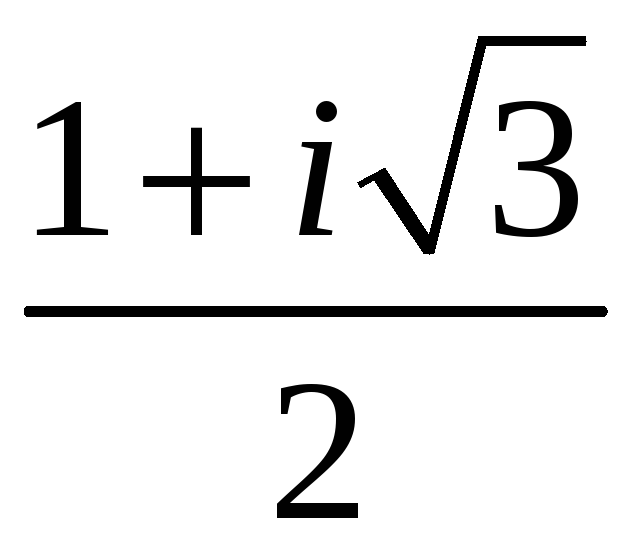5.8.29. Вычислить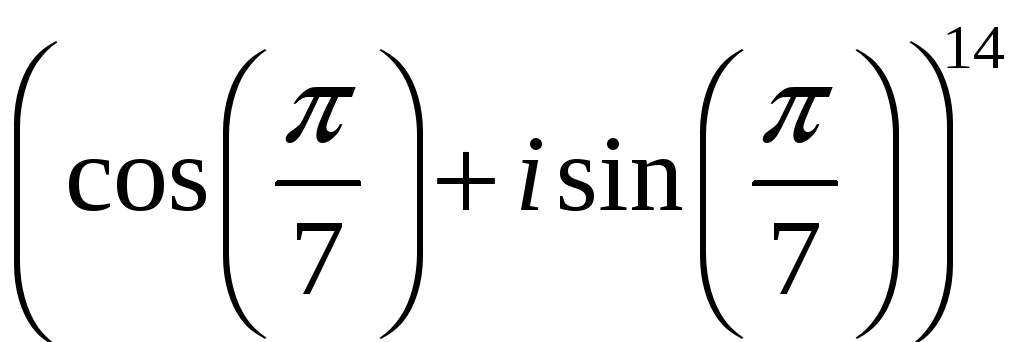
.
#3) 1 .
5.8.30. Вычислить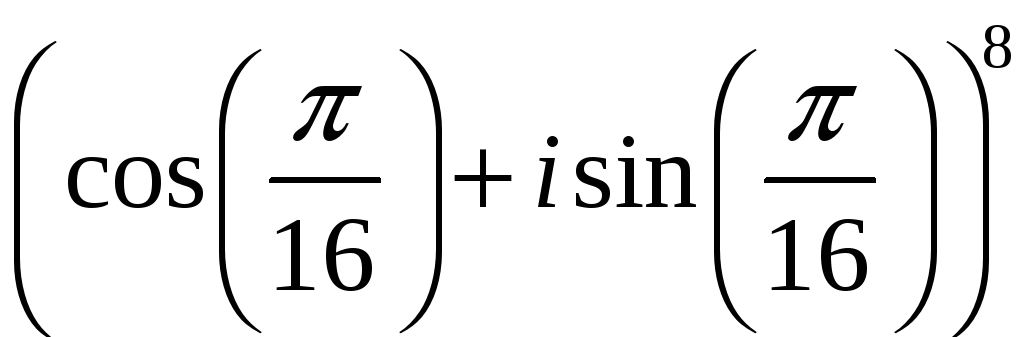
.
#4)
.
5.8.31. Вычислить
.
#5) 0.
5.9. Теория
5.9.1. Функция
называется
гармонической в области
,
если она имеет в ней непрерывные частные
производные второго порядка и удовлетворяет
в этой области уравнению Лапласа
#3)
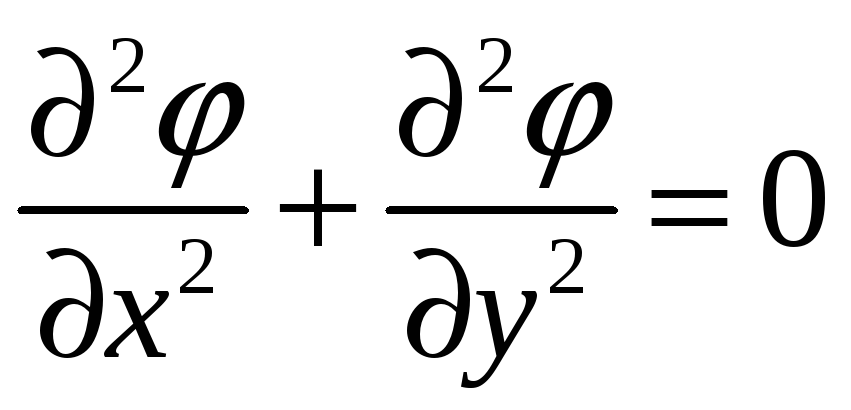
5.9.2. Функция
называется аналитической в точке
,
если она…
#4) дифференцируема в ней и некоторой ее окрестности;
5.9.3. Функция называется аналитической
в области
,
если она ……
#2) дифференцируема в каждой точке этой области;
5.9.4. Если
,
то в каждой точке дифференцируемости
функции выполняются равенства (Коши -
Римана)
#1)
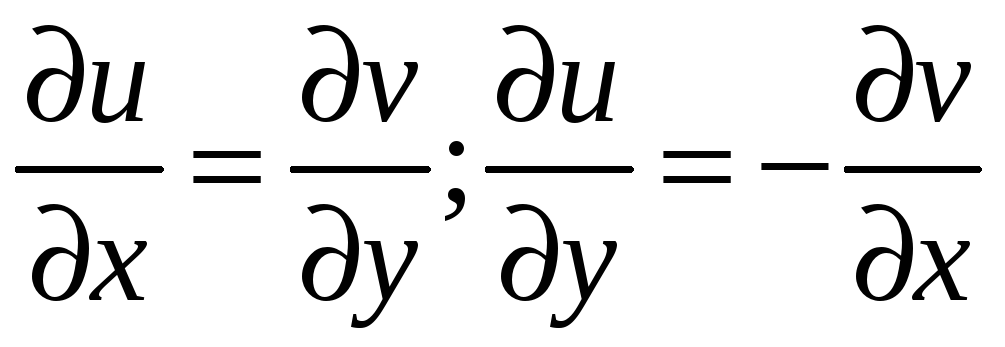
5.9.5. Для всякой аналитической функции
производная
выражается
через частные производные функций
и
#5)
5.9.6. По какой формуле вычисляют интеграл от функции
комплексной переменной
# 3)
5.9.7. Если
- аналитическая функция в односвязной
области D, то значение
интеграла
#4) не зависит от линии Г интегрирования, а только от координат начальной и конечной точки этой линии
5.9.8. Если функция
является аналитической в односвязной
области D, содержащей
точки
,
и
-
первообразная для функции
,
то справедлива формула
#2)
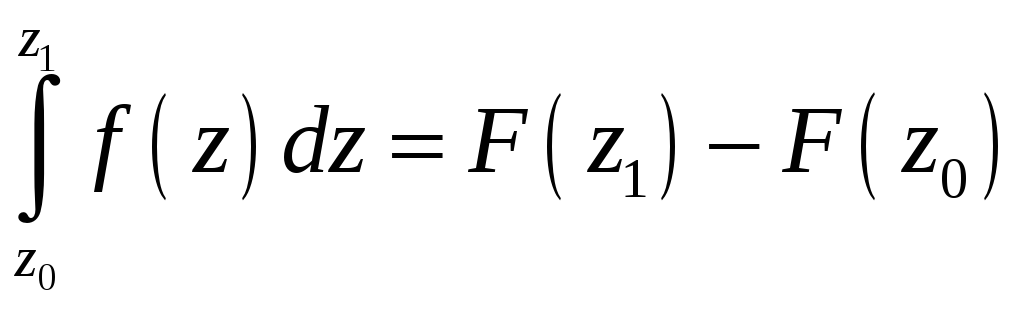
5.9.9. Для всякой функции
аналитической в некоторой односвязной
области D, интеграл
по любому замкнутому кусочно-гладкому
контуру Г, целиком принадлежащему
области D равен
#4) равен нулю
5.9.10. Если функция
является аналитической в некоторой
области D, ограниченной
кусочно-гладким контуром Г, и на самом
контуре, то верна интегральная формула
Коши
#1)
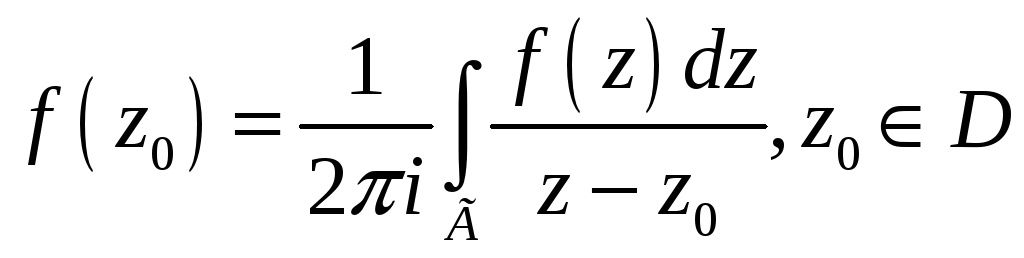
5.9.11. Если функция
является аналитической в некоторой
области D, ограниченной
кусочно-гладким контуром Г, и на самом
контуре, то для любого натурального n
верна формула
#3)
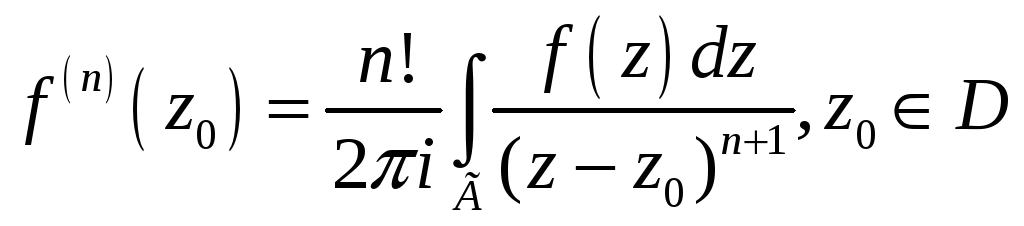
5.9.12. Функция
,однозначная
и аналитическая в точке
,
разлагается в окрестности этой точки
в ряд Тейлора.
#5)
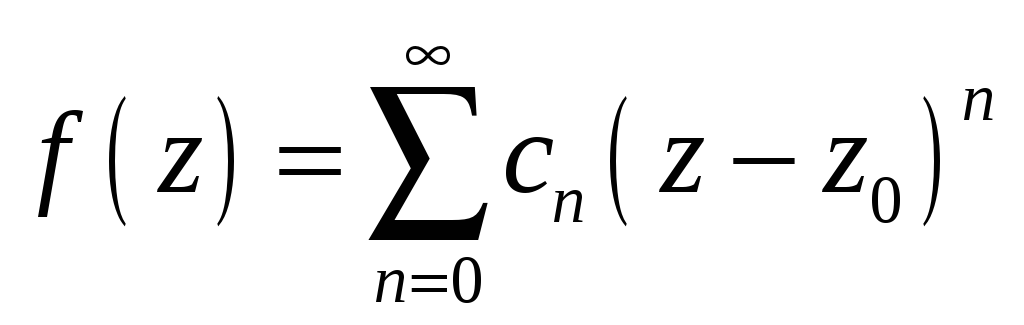
5.9.13. Функция
при
раскладывается
в ряд Тейлора.
#4)
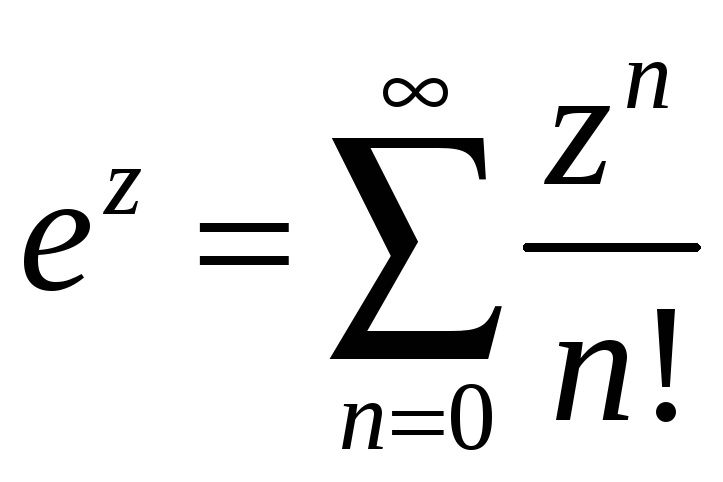
5.9.14. Функция
при
раскладывается
в ряд Тейлора.
#2)
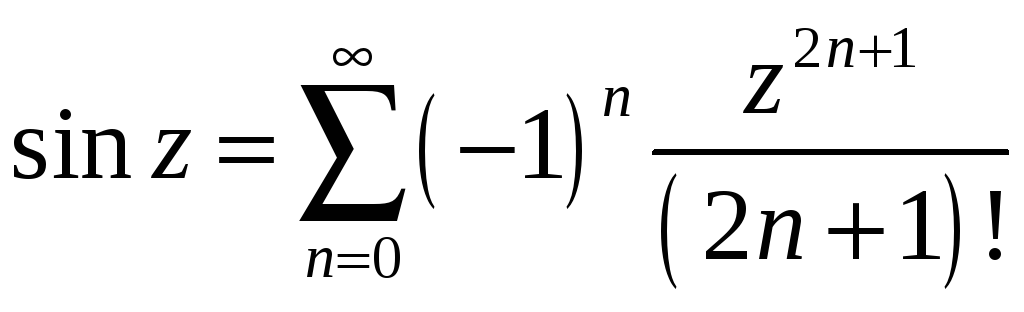
5.9.15. Функция
при
раскладывается
в ряд Тейлора.
#4)
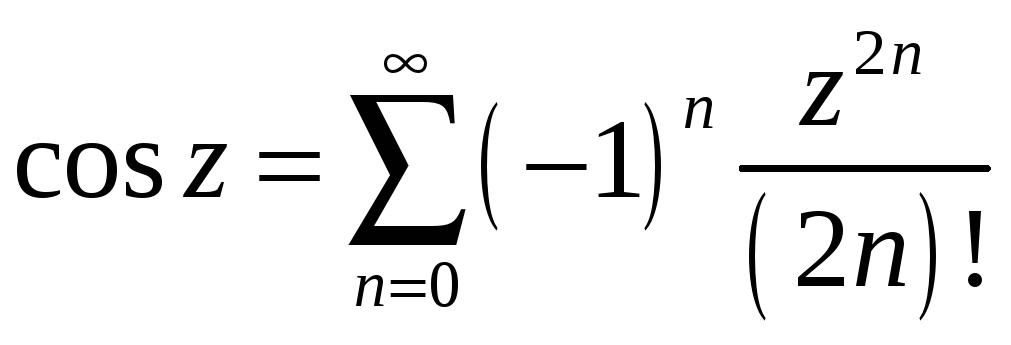
5.9.16. Функция
при
раскладывается
в ряд Тейлора.
#5)
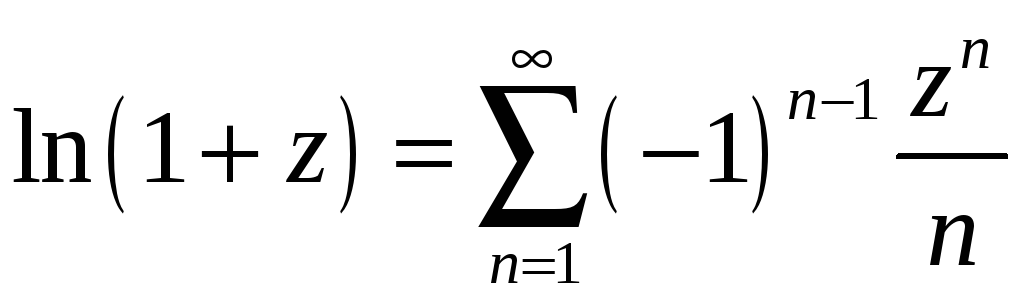
5.9.17. Функция
аналитическая в кольце
представляется в этом кольце сходящимся рядом Лорана
#1)
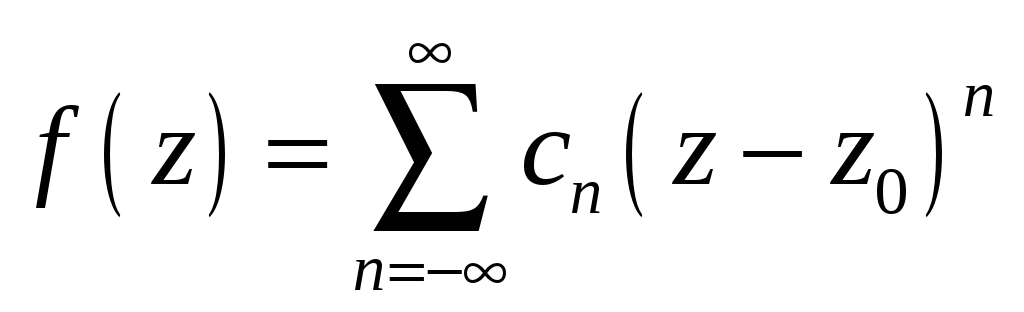
5.9.18. Изолированная особая точка
называется устранимой особой точкой
функции
,
если в разложении в ряд Лорана относительно
этой точки:
1) отсутствует правильная (регулярная) часть разложения
#2) отсутствует главная часть разложения
3) главная часть ряда Лорана содержит, лишь конечное число членов
4) ) главная часть ряда Лорана содержит бесконечное число членов
5)
5.9.19. Изолированная особая точка
называется полюсом функции
,
если в разложении в ряд Лорана относительно
этой точки:
#3) главная часть ряда Лорана содержит, лишь конечное число членов
5.9.20. Изолированная особая точка
называется существенно особой точкой
функции
,
если в разложении в ряд Лорана относительно
этой точки:
#4) главная часть ряда Лорана содержит бесконечное число членов
5.9.21. Вычетом функции
в изолированной особой точке
называется
#1) коэффициент
в разложении в ряд Лорана
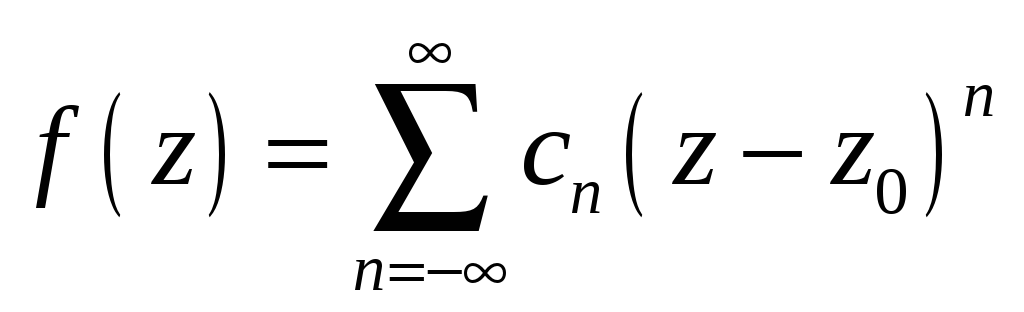
5)
5.9.22. Если
полюс
порядка
,
то вычет
функции
в этой точке находится по формуле
#2)
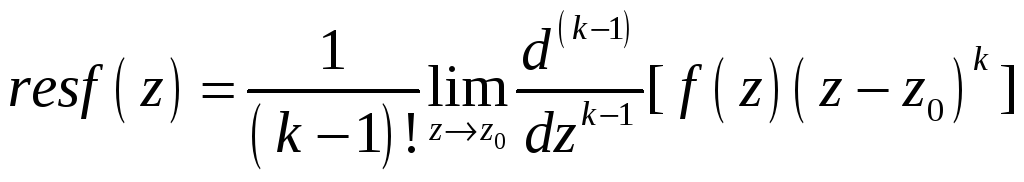
5.9.23. Вычетом функции
в бесконечности
называется
#2) коэффициент
в разложении в ряд Лорана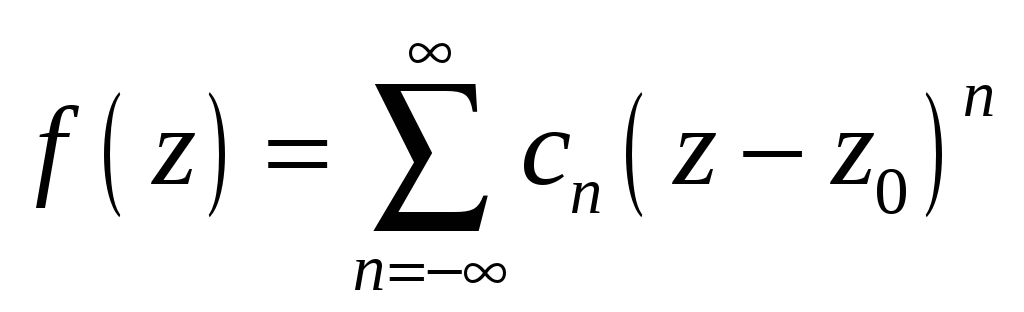
5.9.24. Если функция
аналитическая
внутри замкнутого контура
и на этом контуре за исключением конечного
числа особых точек
,
внутри
,
то
#5)
-
Функция
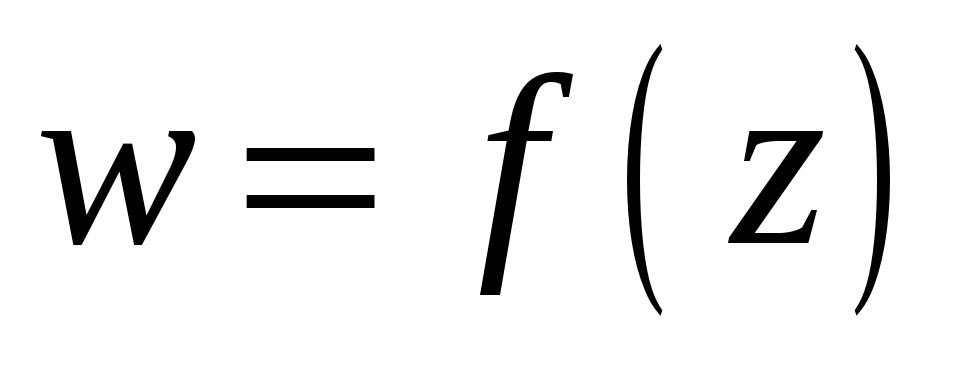является аналитической в бесконечно
удаленной точке
,
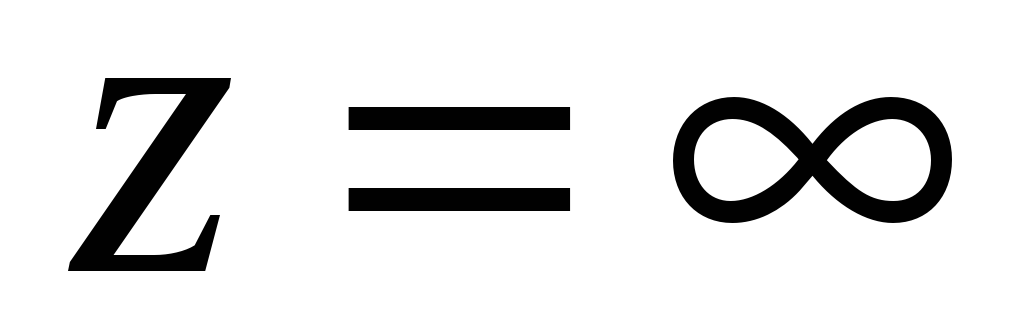если функция
#4)
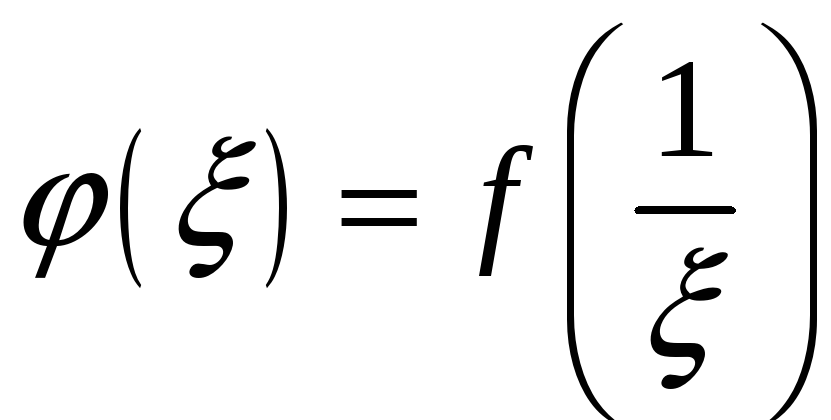аналитична в точке
