2.3. Вектор электрической индукции.

1. Вектор электрической индукции.

По своей физической природе поляризационные заряды – это обычные заряды, создающие в окружающем пространстве электрическое поле. Поэтому теорема Гаусса для вектора в веществе приобретает вид:

(3.1)

или

, (3.2)

где сторонний заряд и плотность сторонних зарядов, и связанный заряд и плотность связанных зарядов, соответственно. Используя формулу (2.10), выражение (3.2) можно переписать в виде:

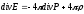, (3.3)

. (3.4)

Аналогично выражение (3.1) может быть представлено в виде:

. (3.5)

Введем новый вектор - вектор электрической индукции (иначе, вектор электрического смещения):

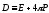. (3.6)

Тогда сразу получаем

, (3.7)

. (3.7а)

(3.7) и (3.7а) - уравнение системы уравнений Максвелла, записанное в интегральной и дифференциальной формах:

Поток вектора электрической индукции через замкнутую поверхность определяется только свободными зарядами, охватываемыми этой поверхностью.

Полученные уравнения являются обобщением теоремы Гаусса для электрического поля в веществе.

В вакууме вектор поляризации равен нулю и .

Примечание: в СИ имеем

.

2.3.2. Диэлектрическая проницаемость.

Электрическое поле в вакууме полностью характеризуется вектором . В тоже время для описания поля в веществе нужно еще знать либо вектор , либо вектор . Поэтому нам понадобится уравнение, определяющее зависимость поляризованности вещества от напряженности электрического поля.

Принципиально возможно, зная атомную структуру вещества, рассчитать смещение электронов и ядер при включении внешнего электрического поля, т.е. вычислить и получить требуемое уравнение. Действительно, в последние годы благодаря развитию методов современной вычислительной физики делаются попытки теоретического расчета. Эти расчеты очень трудоемки, но основная проблема, стоящая на этом пути, заключается в том, что для различных типов веществ не существует универсальной зависимости вектора от напряженности электрического поля .

Однако еще до создания квантовой механики был разработан подход, основанный на нахождении связи между вектором поляризации и напряженностью электрического поля для различных классов диэлектриков эмпирическим путем.

Опыт показывает, что связь между и для обширного класса диэлектриков линейна и однородна.

1) Для изотропных диэлектриков и не слишком больших значений напряженности электрического поля вектор пропорционален и коллинеарен вектору :

(3.8)

Введенный здесь коэффициент называется поляризуемостью диэлектрика (или диэлектрической восприимчивостью), которая зависит от плотности и температуры диэлектрика.

Подставляя в (3.6) выражение (3.8), получаем

. (3.9)

Коэффициент , связывающий вектор электрической индукции с напряженностью электрического поля и равный , называется диэлектрической проницаемостью среды и характеризует индивидуальные свойства диэлектриков.

В вакууме: и .

Примечание: в системе СИ имеем .

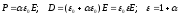2) Анизотропные среды. К таким средам относятся прежде всего кристаллические диэлектрики. Для них, вообще говоря, направления векторов и не совпадают. Поэтому связь между поляризованностью диэлектрика и напряженностью электрического поля выражается более общей линейной однородной зависимостью записывается в более общем виде:

. (3.10)

Здесь - безразмерные коэффициенты, зависящие от выбора координатных осей.

В декартовой системе координат можно записать

. (3.11)

Совокупность этих 9 коэффициентов образует тензор поляризуемости диэлектрика.

Аналогично записывается выражение, связывающее векторы электрической индукции электрической напряженности поля :

, (3.12)

где тензор диэлектрической проницаемости вещества:

(3.13)

где единичный тензор, определяемый условиями:

при и при .

Пользуясь законом сохранения энергии можно показать, что тензоры и симметричны, т.е.

. (3.14)

Т.о., рассматриваемые девятикомпонентные тензоры содержат по 6 независимых величин.

3. Существуют диэлектрики, для которых нет линейной связи между векторами и . К ним относятся некоторые ионные кристаллы и электреты, а также сегнетоэлектрики. У сегнетоэлектриков связь между векторами поляризованности и напряженности электрического поля нелинейная и зависит от предыстории образца, т.е. от предшествующих значений напряженности электрического поля, в котором он находился. Неоднозначная зависимость поляризованности от напряженности приложенного электрического поля называется гистерезисом.

Поведение электретов и аналогичных им видов диэлектриков в электрическом поле можно приближенно описать соотношением вида:

,

где величины и от напряженности электрического поля 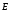не зависят.