Код программы

public partial class Form1 : Form

{

Int32 Ssize = 400;

Pen p = new Pen(Color.Blue);

Bitmap bmp;

Graphics Gr;

Int32 x, y,d;

public Form1()

{

InitializeComponent();

}

private void Clear()

{

bmp = new Bitmap(600, 400);

Gr = Graphics.FromImage(bmp);

Gr.Clear(Color.White);

p.Color = Color.Gray;

p.Width = 2;

pictureBox1.Image = bmp;

}

private void button1_Click(object sender, EventArgs e)

{

Clear();

}

private void Form1_Load(object sender, EventArgs e)

{

Clear();

pictureBox1.Image = bmp;

}

void draw(Int32 a,Int32 x1,Int32 y1)

{

Int32 y2=Convert.ToInt32(Math.Sqrt(a*a-(a/2)*(a/2)));

Gr.DrawLine(p, x1, y1, x1 + a / 2,y-y2);

Int32 x2 = x1 + a/2;

Gr.DrawLine(p, x2, y-y2, x2 + a / 2, y);

d = d / 2;

x = x2 + a / 2;

pictureBox1.Image = bmp;

if (d > 0) { draw(d, x, y); }

}

private void button2_Click(object sender, EventArgs e)

{

x=10;

y=300;

Int32 x2,y2;

d=200;

draw(d, x, y);

}

}

Работа №6 Задание

Нарисовать любой фрактал.

Обзор теории

Фракталы с большой точностью могут описывать многие физические явления и природные образования: горы, облака, деревья, ландшафты... Впервые фрактальную природу нашего мира подметил Бенуа Мандельброт. Слово «фрактал» происходит от латинского fractus, что означает «дробный», и frahgere — «ломать». Главной особенностью фракталов является их бесконечноесамоподобие.

Фрактальные функции широко используются в качестве инструментов для реалистичного построения природных объектов, бесконечно сложных узоров и картин... В машинной графике метод построения фрактальных поверхностей первыми применили Карпентер, Фурнье и Фассел. Итак, фракталы — это функции, которые ведут себя не совсем обычно и могут не подчиняться основным законам поведения «обычных» функций.

Фрактальная поверхность состоит из случайно заданных полигональных или биполиноминальных поверхностей. Одно из преимуществ таких поверхностей в том, что можно получить любой уровень их детализации, независимо от того, насколько близко мы к ним находимся. В машинной графике фракталы строятся простыми и быстрыми итерационными алгоритмами.

Попробуем изобразить линию-фрактал, имеющую бесконечное число максимумов и минимумов на отрезке (0, 1). Такая линия показана на рис. 15.1, ей соответствует следующая функция:

f(x) =		x * cos(p/x), x <> 0
		0, x = 0

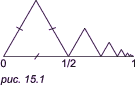
Построить эту функцию можно так: разбиваем отрезок на 1/2, строим равносторонний треугольник; одну из сторон делим на 2 и от него строим следующий треугольник с меньшей стороной и так до бесконечности...

Мы говорим, что функция рекурсивна (или что она основана на рекурсии), если в ней содержится одно или несколько обращений к самой себе или к другим функциям, в которых есть обращения к данной функции. При входе в обычную функцию выход из нее всегда происходит раньше, чем повторный вход, но для рекурсивной функции это необязательно.

Приведем пример простой программы TRIANGLS, строящей на экране компьютера изображение вписанных друг в друга треугольников (рис. 24.1) и использующей для этого рекурсивный вызов функции.

Опишем вкратце алгоритм работы программы. Сначала вычерчивается первый треугольник. После этого вызывается функция tria, строящая внутри этого треугольника малый треугольник так, что вершины его лежат точно на серединах сторон большого треугольника. К малому треугольнику с каждой стороны прилегает по треугольнику. Чтобы построить в них точно такую же картину, достаточно рекурсивно вызвать для каждого функцию tria с координатами вершин малых треугольников в качестве аргументов. В обращение включен целочисленный аргумент n, определяющий глубину рекурсии.

Начнем с некоторого целого числа n, заданного пользователем; этот аргумент устанавливается равным n - 1 для каждого из трех рекурсивных обращений. То есть при достижении «самого глубокого уровня рекурсии», значение n становится равным нулю, что приводит к немедленному возврату в вызывающую функцию, то есть в саму функцию tria.