Фракталы

Взгляните на рис. 24.6. На нем представлена замкнутая кривая, которая называется фрактальной кривой или просто фракталом. Фрактал подобен острову с береговой линией, кажущейся ровной издали, но становящейся совершенно нерегулярной по мере приближения. Фигуру, показанную на рис. 24.6, можно построить с помощью рекурсии, причем с увеличении глубины рекурсии мы получим замкнутую область, граница которой становится очень большой по сравнению с самой областью.

С помощью программы SQFRACT можно получить такую картинку. Первые четыре аргумента функции side программы представляют собой координаты концевых точек A и B отрезка прямой линии. Но этот отрезок будет вычерчен только в том случае, если аргумент n функции side будет равен нулю. В противном случае на этом отрезке будут сформированы две новые точки P и S. Они будут определять концевые точки стороны уменьшенного квадрата (при равенстве PS = f * AB), как показано на (рис. 24.7). Из рисунка очевидно, что координаты точки Q можно вычислить следующим образом:

x_Q = x_P + (y_S - y_P)

y_Q = y_P + (x_S - x_P).

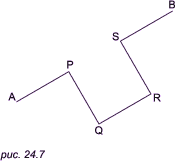
(Напомним, что аналогичный способ формирования новой точки уже обсуждался более подробно при рассмотрении кривой Гильберта). Координаты точки R определяются очень просто, поскольку она находится в таком же отношении к точке Q, как точка S относится к точке P. Теперь можно вычертить отрезок AP, выполнить рекурсивное обращение к функции side для сторон PQ, QR, RS меньшего квадрата и закончить вычерчиванием отрезка SB.

Вместо непосредственного вычерчивания отрезков AP и SB для них можно рекурсивно обратиться к функции side. Хотя в данном конкретном случае это и не дает удовлетворительного результата, но полезна сама идея. Она приводит к целому классу интересных новых кривых, состоящих из отрезков прямых линий, которые, в отличие от рис. 24.6, имеют почти одинаковую длину. (Напомним, что с подобной ситуацией мы встречались в случае кривых Гильберта).

Рассмотрим общую программу FRCURVE для генерации таких кривых. Во-первых, базовая фигура может быть задана либо в виде горизонтального отрезка прямой линии, либо в виде правильного многоугольника. Во-вторых, вместо вычисления позиций новых точек P, Q, R, S («модельных точек») относительно позиций концевых точек A и B, как на рис. 24.7, пользователь в качестве входных данных может задать любое количество таких точек, не обязательно четыре. Введем локальную систему координат, в которой точка A совпадает с точкой начала (0, 0), а точка B — с точкой (1, 0). Тогда позиции модельных точек могут быть выражены в этих локальных координатах. Рассмотрим для примера рис. 24.8, где определены три новые точки с координатами (x, y): (0.45, 0), (0.50, 0.45) и (0.55, 0).

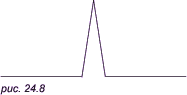
Напомним, что обе концевые точки A(0, 0) и B(1, 0) неявно добавляются к модельным точкам, которые мы должны ввести, поэтому вообще число модельных точек всегда на две точки больше, чем заданное число. Если же всю фигуру целиком применять к каждой из ее четырех частей, то получим рис. 24.9 и так далее.

Поскольку мы можем задать правильный многоугольник, например, с четырьмя сторонами, то программа FRCURVE, в которой реализована эта операция, сформирует изображение, показанное на рис. 24.10.