4. Понятие меры информации (энтропии), алгоритм Хаффмана.

Наиболее широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой разной природы, получил подход. К. Шеннона. Рассмотрим следующую ситуацию.

Источник передает элементарные сигналы k различных типов. Проследим за достаточно длинным отрезком сообщения. Пусть в нем имеется N₁ сигналов первого типа, N₂ сигналов второго типа, ..., N_k сигналов k-го типа, причем N₁ + N₂ + ... + N_k = N – общее число сигналов в наблюдаемом отрезке, f₁, f₂, ..., f_k – частоты соответствующих сигналов. При возрастании длины отрезка сообщения каждая из частот стремится к фиксированному пределу, т.е.

lim f_i = p_i, (i = 1, 2, ..., k),

где р_i можно считать вероятностью сигнала. Предположим, получен сигнал i-го типа с вероятностью р_i, содержащий – log p_i единиц информации. В рассматриваемом отрезке i-й сигнал встретится примерно Np_i раз (будем считать, что N достаточно велико), и общая информация, доставленная сигналами этого типа, будет равна произведению Np_i log р_i. То же относится к сигналам любого другого типа, поэтому полное количество информации, доставленное отрезком из N сигналов, будет примерно равно

Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е. удельную информативность источника, нужно это число разделить на N. При неограниченном росте приблизительное равенство перейдет в точное. В результате будет получено асимптотическое соотношение – формула Шеннона

Если в формуле Шеннона принять, что

р₁ = p₂ = ... = р_i = ... =p_N = 1/N, то

Знак минус в формуле Шеннона не означает, что количество информации в сообщении – отрицательная величина. Объясняется это тем, что вероятность р, согласно определению, меньше единицы, но больше нуля. Так как логарифм числа, меньшего единицы, т.е. log p_i – величина отрицательная, то произведение вероятности на логарифм числа будет положительным.

Кроме этой формулы, Шенноном была предложена абстрактная схема связи, состоящая из пяти элементов (источника информации, передатчика, линии связи, приемника и адресата), и сформулированы теоремы о пропускной способности, помехоустойчивости, кодировании и т.д.

В результате развития теории информации и ее приложений идеи Шеннона быстро распространяли свое влияние на самые различные области знаний. Было замечено, что формула Шеннона очень похожа на используемую в физике формулу энтропии, выведенную Больцманом. Энтропия обозначает степень неупорядоченности статистических форм движения молекул. Энтропия максимальна при равновероятном распределении параметров движения молекул (направлении, скорости и пространственном положении). Значение энтропии уменьшается, если движение молекул упорядочить. По мере увеличения упорядоченности движения энтропия стремится к нулю (например, когда возможно только одно значение и направление скорости). При составлении какого-либо сообщения (текста) с помощью энтропии можно характеризовать степень неупорядоченности движения (чередования) символов. Текст с максимальной энтропией – это текст с равновероятным распределением всех букв алфавита, т.е. с бессмысленным чередованием букв, например: ЙХЗЦЗЦЩУЩУШК ШГЕНЕЭФЖЫЫДВЛВЛОАРАПАЯЕЯЮЧБ СБСЬМ. Если при составлении текста учтена реальная вероятность букв, то в получаемых таким образом «фразах» будет наблюдаться определенная упорядоченность движения букв, регламентируемая частотой их появления: ЕЫТ ЦИЯЬА ОКРВ ОДНТ ЬЧЕ МЛОЦК ЗЬЯ ЕНВ ТША.

При учете вероятностей четырехбуквенных сочетаний текст становится настолько упорядоченным, что по некоторым формальным признакам приближается к осмысленному: ВЕСЕЛ ВРАТЬСЯ НЕ СУХОМ И НЕПО И КОРКО. Причиной такой упорядоченности в данном случае является информация о статистических закономерностях текстов. В осмысленных текстах упорядоченность, естественно, еще выше. Так, в фразе ПРИШЛ... ВЕСНА мы имеем еще больше информации о движении (чередовании) букв. Таким образом, от текста к тексту увеличиваются упорядоченность и информация, которой мы располагаем о тексте, а энтропия (мера неупорядоченности) уменьшается.

Алгоритм Хаффмана.

Хаффмановское кодирование появилось в 1952 году. Главное его предназначение заключалось в упаковке текстовых файлов - для другого он мало приспособлен. Имеет довольно простую реализацию, так что его вполне удобно использовать в устройствах имеющих слабые микропроцессоры.

Алгоритм основан на том факте, что некоторые символы из стандартного 256-символьного набора в произвольном тексте могут встречаться чаще среднего периода повтора, а другие, соответственно, – реже. Следовательно, если для записи распространенных символов использовать короткие последовательности бит, длиной меньше 8, а для записи редких символов – длинные, то суммарный объем файла уменьшится.

Хаффман предложил очень простой алгоритм определения того, какой символ необходимо кодировать каким кодом для получения файла с длиной, очень близкой к его энтропии. Пусть у нас имеется список всех символов, встречающихся в исходном тексте, причем известно количество появлений каждого символа в нем. Выпишем их вертикально в ряд в виде ячеек будущего графа по правому краю листа. Выберем два символа с наименьшим количеством повторений в тексте (если три или большее число символов имеют одинаковые значения, выбираем любые два из них). Проведем от них линии влево к новой вершине графа и запишем в нее значение, равное сумме частот повторения каждого из объединяемых символов. Отныне не будем принимать во внимание при поиске наименьших частот повторения два объединенных узла (для этого сотрем числа в этих двух вершинах), но будем рассматривать новую вершину как полноценную ячейку с частотой появления, равной сумме частот появления двух соединившихся вершин. Будем повторять операцию объединения вершин до тех пор, пока не придем к одной вершине с числом. Для проверки: очевидно, что в ней будет записана длина кодируемого файла. Теперь расставим на двух ребрах графа, исходящих из каждой вершины, биты 0 и 1 произвольно – например, на каждом верхнем ребре 0, а на каждом нижнем – 1. Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до нее, выписывая нули и единицы по маршруту следования. Для рисунка символ "А" получает код "000", символ "Б" – код "01", символ "К" – код "001", а символ "О" – код "1".

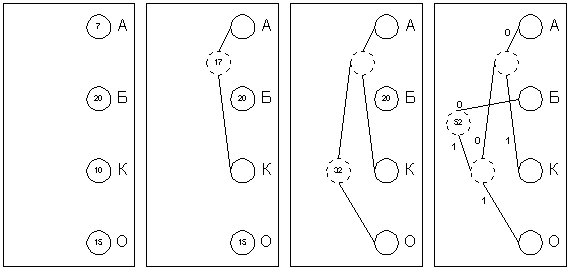
В теории кодирования информации показывается, что код Хаффмана является префиксным, то есть код никакого символа не является началом кода какого-либо другого символа. Проверьте это на нашем примере. А из этого следует, что код Хаффмана однозначно восстановим получателем, даже если не сообщается длина кода каждого переданного символа. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации. Например, при приеме "0100010100001" им сначала отделяется первый символ "Б": "01-00010100001", затем, снова начиная с вершины дерева – "А" "01-000-10100001", затем аналогично декодируется вся запись "01-000-1-01-000-01" "БАОБАБ".

Классический алгоритм Хаффмана имеет один недостаток: для восстановления содержимого сжатого сообщения декодер должен знать таблицу частот появления символов, которая должна высылаться впереди данных.