24.Методы минимизации функции одной переменной: оптимальный пассивный поиск, метод деления отрезка пополам.

Одно из важнейших направлений в проектировании и эксплуатации технологических процессов состоит в оптимизации (минимизации или максимизации) некоторой характеристики f(x). Функцию f(x) называют целевой функцией. Основное внимание уделяют минимизации целевой функции, так как максимизация сводится к минимизации с помощью введения новой целевой функции z(x) = - f(x). В случае, когда изменяется один скалярный параметр х, возникает задача одномерной минимизации, то есть f(x) — действительная функция одной переменной, определенная на множестве R.

Существуют различные постановки задачи минимизации:

• найти все точки локального минимума и отвечающие им значения функции;

• вычислить конкретную точку локального минимума или точку глобального минимума;

• найти минимальное значение целевой функции, независимо от того, в какой именно точке оно достигается.

Для того чтобы применить один из алгоритмов минимизации, следует предварительно найти отрезок [а, b], содержащий точку х* на котором она является единственной точкой локального минимума. Этот отрезок называется отрезком локализации точки х*

Пусть f(x) — функция, определенная на отрезке [а, b] . Предположим, что на этом отрезке содержится единственная точка х* локального минимума функции f(x) , причем функция строго убывает при х < х* и строго возрастает при х > х*. Такая функция называется унимодальной.

Ряд методов минимизации основан на сравнении значений функции/ в точках х₁ х_2,..., х_п. Эти методы называются методами прямого поиска, а точки х_i - пробными точками.

Пусть требуется найти приближение х * к точке минимума х* функции f унимодальной на отрезке [а, b]; число пробных точек п заранее фиксируется и за приближение х* к точке минимума принимается одна из этих точек.

Оптимальный пассивный поиск. Метод, в котором задается правило вычисления сразу всех

пробных точек х₁ х_2,..., х_п и за х* принимается та точка х^ для которой f(x_k) = min f(x_i)называется методом пассивною поиска. ^1<i<N

Если точки х₁ х_2,..., х_п расположить на отрезке [а, b] равномерно в соответствии с формулой

,где то метод с таким выбором пробных точек называется оптимальным пассивным поиском.

Метод деления отрезка пополам. Пусть для решения поставленной задачи последовательно вычисляются значения функции f в n пробных точках х₁ х_2,..., х_п причем для определения каждой из

точек x_k можно использовать информацию о значениях функции во всех предыдущих точках x_h х₂

x_k-1. Соответствующие методы называют методами последовательного поиска. Простейший из методов этого семейства — метод деления отрезка пополам. В нем используется принцип последовательного сокращения отрезка локализации. Оценить погрешность можно по формуле:

где - длина отрезка локализации на n-ном шаге,

параметр метода.

Вычисления с точностью до заданного е>0 прекращают, как только выполнится неравенство

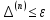
25.Многомерные методы оптимизации.

Пусть целевая функция z - f(x₁ x₂,..._t х_т) — действительная функция многих переменных, определенная на множестве X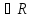. Тогда задача оптимизации этой функции является многомерной. В случае, когда ограничения на переменные x₁ x₂,..._t х_т отсутствуют, говорят о задаче безусловной минимизации. В противном случае говорят о задаче условной минимизации.

Большинство методов решения задач безусловной минимизации на самом деле являются методами поиска точки локального минимума, так как для нахождения точки глобального минимума определяют все точки локального минимума и вычисляют значения функции в них, а затем выбирают минимальное значение. Но такой подход связан с очень большими вычислениями. На практике чаще используют другой подход: определить местоположение точки глобального минимума из анализа самой задачи, а затем применить для вычисления один из методов поиска точки локального минимума.

Большинство итерационных методов, применяемых для решения задачи безусловной минимизаций функций многих переменных, относятся к классу методов спуска, т. е. таких методов, для которых каждая итерация (шаг) приводит к уменьшению значения целевой функции: для всех п>0. На каждой итерации метода спуска находят ненулевой вектор, называемый направлением спуска и вычисляют шаг спуска. Далее находят приближение Х^(п+1) и проверяют выполнение критерия окончания итераций. Последовательность точек, генерируемую методом спуска, называют траекторией спуска.

Покоординатный спуск.

В методе покоординатного спуска в качестве очередного направления спуска выбирают направление одной из координатных осей. Наиболее известным является метод циклического покоординатного спуска.

Пусть приближение X⁽ⁿ⁾ уже найдено.

Цикл с номером, n + 1 состоит из т шагов. На первом шаге производят спуск по координате x₁. Значения х₂ = остальных координат фиксируют, а выбирают из условия

Фактически решается задача минимизации функции одной переменной

На втором шаге производят спуск по координате Значения х₁ = остальных координат фиксируют и выбирают как решение задачи одномерной минимизации по переменной. Аналогично осуществляют остальные шаги. На последнем m-м шаге координату определяют из условия минимизации функции по переменной х_т. В результате получается очередное приближение в точке минимума. Далее цикл метода снова повторяют пока не выполнится критерий окончания итераций.

20