22.Метод Рунге - Кутта.

Основная идея метода: В рабочих формулах нужно использовать саму функцию f(x;y) и на каждом шаге вычислять её значения в нескольких точках. Пусть дано диф. ур-ие по методу Эйлера выразим

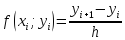
. Т.к. для вычисления производной взяты 2 точки N_i и N_(i+1) то лучшим приближением правой части диф. ур-ия будет значение , тогда полученные ур-ия относительно можно решать, взяв в качестве начального приближения значения от метода эйлера получим:

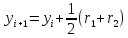, где

Формы метода Рунге-Кута 2-го порядка.

Чем выше порядок формул Рунге-Кута, тем более точное значение они дают. Наиболее распространёнными являются формулы 4-го порядка.

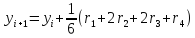, где

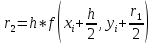
Оценить погрешность можно с помощью метода двойного счёта

Допустим – точное решение уравнения , тогда для формул Рунге-Кута 4-ого порядка , где k-шаг, с которого вычислено приближённое значение, точно так же при решении с шагом получим:

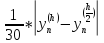= при достаточно малом шаге h и малой погрешности вычислений решение диф. ур-ия методом Рунге-Кута 4-ого порядка будет близким к точному.

Пусть при решении диф. ур-ия строится таблица с шагом h и аргументами для них находят соответствующие значения

Для тех же аргументов находят улучшенные приближения тогда для метода Эйлера

Для модификации метода Эйлера:

23.Методы минимизации функции одной переменной: метод Фибоначчи, метод золотого сечения.

Одно из важнейших направлений в проектировании и эксплуатации технологических процессов состоит в оптимизации (минимизации или максимизации) некоторой характеристики f(x). Функцию f(x) называют целевой функцией. Основное внимание уделяют минимизации целевой функции, так как максимизация сводится к минимизации с помощью введения новой целевой функции z(x) = - f(x). В случае, когда изменяется один скалярный параметр х, возникает задача одномерной минимизации, то есть f(x) — действительная функция одной переменной, определенная на множестве R.

Существуют различные постановки задачи минимизации:

• найти все точки локального минимума и отвечающие им значения функции;

• вычислить конкретную точку локального минимума или точку глобального минимума;

• найти минимальное значение целевой функции, независимо от того, в какой именно точке оно достигается.

Для того чтобы применить один из алгоритмов минимизации, следует предварительно найти отрезок [а,b], содержащий точку х* на котором она является единственной точкой локального минимума. Этот отрезок называется отрезком локализации точки х*.

Пусть f(x) — функция, определенная на отрезке [а, b] . Предположим, что на этом отрезке содержится единственная точка х* локального минимума функции f(x) , причем функция строго убывает при х х* и строго возрастает при х х*. Такая функция называется унимодальной.

Ряд методов минимизации основан на сравнении значений функции f в точках x₁ х₂,…, x_n. Эти методы называются методами прямого поиска, а точки х, - пробными точками.

Пусть требуется найти приближение х * к точке минимума х* функции f, унимодальной на отрезке [а, b]. число пробных точек п заранее фиксируется и за приближение х* к точке минимума принимается одна из этих точек.

Метод деления отрезка пополам требует на каждой итерации вычисления двух новых значений функции. Наблюдения приводят к методам, требующим на каждой итерации (кроме первой) расчета лишь одного нового значения функции. Два наиболее известных среди них — методы Фибоначчи и золотого сечения.

Метод Фибоначчи. Метод Фибоначчи является оптимальным последовательным методом, т. е. методом, обеспечивающим максимальное сокращение отрезка локализации при заданном числе N вычислений функции. Этот метод основан на использовании чисел Фибоначчи F„, задаваемых рекуррентной формулой F_n = F_n-1 + F_n-2 (п2) и начальными значениями F_o=1,F₁=1. Метод Фибоначчи состоит из N-1 шагов.

Метод золотого сечения. Из-за недостатков вместо метода Фибоначчи чаще используется почти столь же эффективный метод золотого сечения.

Золотым сечением отрезка называется такое разбиение отрезка на две неравные части, что отношение длины всего отрезка к длине его большей части равно отношению длины большей части к длине меньшей части отрезка.

Золотое сечение отрезка [а, b] осуществляется каждой из двух симметрично расположенных относительно центра отрезка точек

,

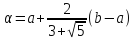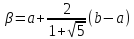
Точка а осуществляет золотое сечение не только отрезка [а, b], но и отрезка [а, β],

Точно так же точка β осуществляет золотое сечение не только отрезка [а, b], но и отрезка [а, b]. Этот факт используется в данном методе.