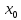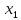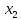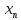- •1. Источники и классификация погрешностей
- •2. Постановка задачи приближённого решения алгебраических уравнен
- •3. Метод половинного деления.
- •4. Метод хорд
- •5. Метод касательной
- •6. Комбинированный метод хорд и касательных
- •7. Решение систем линейных алгебраических уравнений методом Гаусса
- •8. Вычисление определителя и обратной матрицы методом Гаусса
- •9. Решение систем уравнений методом простой итерации
- •10. Метод Зейделя
- •11. Постановка задачи аппроксимации функций
- •12. Интерполяционный многочлен Лагранжа
- •13. Интерполяционные многочлены Ньютона
- •14.Интерполяция сплайнами.
- •15.Квадратурные формулы Ньютона - Котеса. Формула трапеций.
- •16.Квадратурные формулы Ньютона - Котеса. Формула Симпсона.
- •Формула Симпсона
- •17.Квадратурные формулы Гаусса.
- •19.Метод Эйлера.
- •20.Модификации метода Эйлера. Метод Эйлера - Коши.
- •21.Модификации метода Эйлера. Метод серединных точек.
- •22.Метод Рунге - Кутта.
- •23.Методы минимизации функции одной переменной: метод Фибоначчи, метод золотого сечения.
- •24.Методы минимизации функции одной переменной: оптимальный пассивный поиск, метод деления отрезка пополам.
- •25.Многомерные методы оптимизации.
12. Интерполяционный многочлен Лагранжа
Пусть узлы таблицы
|
x |
|
|
|
|
|
|
f(x) |
|
|
|
|
|
Расположены произвольным образом. Интерполяционным многочленом будем искать в виде:
 =
=
 …(x-
…(x- )+
)+ (x-
(x- )(x-
)(x- )(x-
)(x-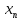 )+…+
)+…+ (x-
(x- )…(x-
)…(x- ),
Коэффициенты
),
Коэффициенты
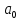 ,
, …
… подберем так, чтобы выполнялось условие:
подберем так, чтобы выполнялось условие:
 (
(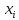 )
=
)
=
 (i=0,1..n)
При x=
(i=0,1..n)
При x= все слагаемы формулы
все слагаемы формулы
 =
=
 …(x-
…(x- )+
)+ (x-
(x- )(x-
)(x- )(x-
)(x- )+…+
)+…+ (x-
(x- )…(x-
)…(x- )
начиная со второго равного 0, следовательно
x=
)
начиная со второго равного 0, следовательно
x= :
:
 (
( )=
)= (
( -
-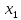 )…(
)…( -
- )=
)= ,
тогда
,
тогда
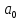 =
= .
При x=
.
При x= останется только второе слагаемое, из
него найдем
останется только второе слагаемое, из
него найдем
 =
= ;
;
 Подставим найденные коэффициенты в
формулу
Подставим найденные коэффициенты в
формулу
 =
=
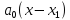 …(x-
…(x- )+
)+ (x-
(x- )(x-
)(x- )(x-
)(x- )+…+
)+…+ (x-
(x- )…(x-
)…(x- )
и получим выражение для интерполяционного
многочлена Лагранжа .
)
и получим выражение для интерполяционного
многочлена Лагранжа . =
= ;
;
 =
= +
+ ;
;
 =
= +
+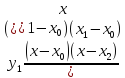 +
+ .
.
13. Интерполяционные многочлены Ньютона
Пусть для функции f задана таблица
|
x |
|
|
|
|
|
|
f(x) |
|
|
|
|
|
В
которой табличные аргументы отличаются
на постоянную величину h>0.
Конечные разности первого порядка –
это разности между соседними табличными
элементами функции.
 =
= -
- .
Конечные разности второго порядка
.
Конечные разности второго порядка
 =
= -
- .
Формула конечных разностей k-ого
порядка k>1
.
Формула конечных разностей k-ого
порядка k>1
 =
= -
- (i=0,1…,n-k)
(i=0,1…,n-k)

По
таблице конечных разностей находят
наилучшую степень интерполирования.
Если конечная разность k-ого
порядка на каком-то участке почти
постоянны, то составляют многочлен k-ой
степени. Будем искать много член n-ой
степени в виде:
 …(x-
…(x-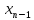 ).
Коэффициенты
).
Коэффициенты
 ;
;
 …
…
 =
= .
x=
.
x= :
:
 =
= ;
x=
;
x= :
:
 =
= ,
h=
,
h= .
.
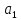 =
= =
=

Подставим
значения
 получим первый интерполяционный
многочлен Ньютона:
получим первый интерполяционный
многочлен Ньютона:
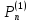 =
= +
+ (x-
(x- )+
)+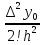 (x-
(x- )(x-
)(x- )+…+
)+…+ (x-
(x-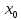 )…(x-
)…(x- ).
Первая интерполяционная формула Ньютона:
f(x)
).
Первая интерполяционная формула Ньютона:
f(x) (x).
x
(x).
x [a;b].
Пусть t=
[a;b].
Пусть t= x=
x=
14.Интерполяция сплайнами.
Применяется при большом количестве узлов функции Sm(x) называется интерполяционным сплайном порядка m для ф-ии f(x) заданной таблицей, если выполняются условия:
|
x |
X0 |
X1 |
… |
xn |
|
f(x) |
y0 |
y1 |
… |
yn |
-
на каждом отрезке [xi; xi+1] (i=0,1,…n-1) функция S(x) является многочленом порядка m
-
S(x)и её производные до (m-1) включительно непрерывны на отрезке [x0; xn]
-
S(xi)=y1 (i=0,1,…,n)
Кубический сплайн можно представить в виде:

Где
 *
*
Из п.3 определения сплайна или формулы * найдём коэффициент ai

Обозначим
через
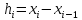 (шаг таблицы) тогда можно получить
равенство:
(шаг таблицы) тогда можно получить
равенство:
 1
1
Из п.2 определения сплайна получим:
 (i=0,1,…,n-1)
(i=0,1,…,n-1)
Учитывая введённые обозначение дифференцируем формулу *
 (i=2,…,n)
2
(i=2,…,n)
2
Из
п.2 определения сплайна
 следовательно
следовательно
 (i=2,…,n)
3
(i=2,…,n)
3
Определим дополнительные условия:
 т.е.
т.е.
 или
или
 4
4
Первое ур-ие системы 4 формально совпадает с формулой 3 при i=0если ввести коэффициент C0 =0
Совокупность равенств 1-4 образуют систему линейных уравнений.
Для построения сплайна необходимо:
-
Сначала находят набор коэффициентов {Ci}для чего в систему уравнений 1-4 преобразуют к виду:

-
Потом находят набор коэф. {di}

-
Потом находят набор коэф. {b1}

-
коэф {a1}известны

Найденные коэффициенты подставляют в формулу * и записывают весь сплайн.