
- •1. Источники и классификация погрешностей
- •2. Постановка задачи приближённого решения алгебраических уравнен
- •3. Метод половинного деления.
- •4. Метод хорд
- •5. Метод касательной
- •6. Комбинированный метод хорд и касательных
- •7. Решение систем линейных алгебраических уравнений методом Гаусса
- •8. Вычисление определителя и обратной матрицы методом Гаусса
- •9. Решение систем уравнений методом простой итерации
- •10. Метод Зейделя
- •11. Постановка задачи аппроксимации функций
- •12. Интерполяционный многочлен Лагранжа
- •13. Интерполяционные многочлены Ньютона
- •14.Интерполяция сплайнами.
- •15.Квадратурные формулы Ньютона - Котеса. Формула трапеций.
- •16.Квадратурные формулы Ньютона - Котеса. Формула Симпсона.
- •Формула Симпсона
- •17.Квадратурные формулы Гаусса.
- •19.Метод Эйлера.
- •20.Модификации метода Эйлера. Метод Эйлера - Коши.
- •21.Модификации метода Эйлера. Метод серединных точек.
- •22.Метод Рунге - Кутта.
- •23.Методы минимизации функции одной переменной: метод Фибоначчи, метод золотого сечения.
- •24.Методы минимизации функции одной переменной: оптимальный пассивный поиск, метод деления отрезка пополам.
- •25.Многомерные методы оптимизации.
4. Метод хорд
Пусть выполняются следующие условия: f(a)*f(b)<0, функция f имеет непрерывные производные f ΄ ≠ 0 и f ̀̀̀ ̀≠ 0, которые сохраняют постоянный знак на отрезке [a,b] Пусть f ΄ > 0 и f ̀̀̀ ̀> 0 на [a,b], тогда f(a)<0 и f(b)>0.
Пусть
 =а
начальное приближение через точки
=а
начальное приближение через точки
 и В проведем хорду. Ее уравнение
и В проведем хорду. Ее уравнение
 =
= Пусть у=0 и х=
Пусть у=0 и х= ,
тогда
,
тогда
 =
= -
- *f(
*f( ).
Через точку
).
Через точку
 (
(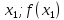 )
и B
(b;f(b))
проведем хорду. Из ее уравнения при у=0
получим
)
и B
(b;f(b))
проведем хорду. Из ее уравнения при у=0
получим
 =
= -
- *f(
*f( )
и т.д. Таким образом получим итерационную
последовательность, которая вычисляется
рекуррентной формулой.
)
и т.д. Таким образом получим итерационную
последовательность, которая вычисляется
рекуррентной формулой.
 =
= -
- *f(
*f(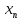 ).
N=0,1…
).
N=0,1…
 =a.
Эта формула верна и для случая, когда f
̀<0 и f
̀̀ ̀ <0 причем
=a.
Эта формула верна и для случая, когда f
̀<0 и f
̀̀ ̀ <0 причем
 =a.
Если f
̀и f
̀̀ ̀ различны, то за
=a.
Если f
̀и f
̀̀ ̀ различны, то за
 =b
и рекуррентная формула имеет вид:
=b
и рекуррентная формула имеет вид:
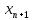 =
=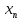 -
-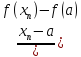 *f(
*f( ).
Погрешность вычисляется по формуле: |
t
-
).
Погрешность вычисляется по формуле: |
t
-
 |
| ((M-m)/m)*|
((M-m)/m)*|
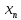 -
- |
n=0,1…,
где 0
|
n=0,1…,
где 0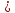 m
m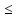 |
f
΄(x)
|
|
f
΄(x)
| M
для x
M
для x [a;b]
[a;b]
5. Метод касательной
Пусть
выполняются следующие условия:
f(a)*f(b)<0,
функция f
имеет непрерывные производные f
΄ ≠ 0 и f
̀̀̀ ̀≠ 0, которые сохраняют постоянный
знак на отрезке [a,b]
t [a;b].
Рекуррентная формула имеет вид:
[a;b].
Рекуррентная формула имеет вид:
 =
= -
- ,
n=0,1,2…
Формула справедлива для всех случаев
относительных знаков f
,
n=0,1,2…
Формула справедлива для всех случаев
относительных знаков f (x)
и f
''(x)
на отрезке [a,b].
Правило выбора начального приближения:
1. Если f
' и f
'' одного знака, то
(x)
и f
''(x)
на отрезке [a,b].
Правило выбора начального приближения:
1. Если f
' и f
'' одного знака, то
 =b.
2. Если f
' и f
'' разных знаков, то
=b.
2. Если f
' и f
'' разных знаков, то
 =a.
Погрешность
вычисляется по формуле:
|t-
=a.
Погрешность
вычисляется по формуле:
|t- |
| (
( )^2.
0<m
)^2.
0<m ; 0<|f
''(x)|
; 0<|f
''(x)| для [a,b].
для [a,b].

6. Комбинированный метод хорд и касательных
Обозначим
приближения метода хорд через
 ,
а приближения метода касательных через
,
а приближения метода касательных через

 или
или
 ,
причем
,
причем
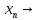 t
и
t
и
 при n
при n .
Процесс уточнения до
.
Процесс уточнения до
 >0
можно остановить как только окажется
|
>0
можно остановить как только окажется
|
 и взяв в качестве приближенного корня
середину отрезка между
и взяв в качестве приближенного корня
середину отрезка между
 и
и
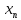 ,
т.е. t
,
т.е. t =
=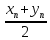 ,
когда вычисления ведутся без заданной
степени точности, то абсолютную
погрешность вычисляют по формуле:
,
когда вычисления ведутся без заданной
степени точности, то абсолютную
погрешность вычисляют по формуле:
 =
= ,
Комбинированный метод дает возможность
ускорить процесс уточнения корней. Для
этого при вычислении
,
Комбинированный метод дает возможность
ускорить процесс уточнения корней. Для
этого при вычислении
 метод хорд вместо соответствующего
неподвижного конца отрезка [a;b]
используют приближение
метод хорд вместо соответствующего
неподвижного конца отрезка [a;b]
используют приближение
 найденное
методом касательных. Вычисление пары
чисел (
найденное
методом касательных. Вычисление пары
чисел (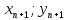 )
начинают с
)
начинают с
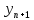 ,
которое определяется формулой метода
касательных
,
которое определяется формулой метода
касательных
 =
= n=0,1,2…
при соответствующем начальном приближении
n=0,1,2…
при соответствующем начальном приближении
 .
Затем находят
.
Затем находят
 по формуле метода хорд (во всех случаях
относительно знаков производных)
по формуле метода хорд (во всех случаях
относительно знаков производных)
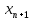 =
=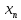 -
- (n=0,1,2…).
Если f
' и f
'' одного знака, то
(n=0,1,2…).
Если f
' и f
'' одного знака, то
 =a
и
=a
и
 =b,
если разных, то
=b,
если разных, то
 =b
и
=b
и
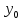 =a.
=a.
7. Решение систем линейных алгебраических уравнений методом Гаусса
Система n линейных уравнений с n независимыми имеет вид:
 +
+ +…+
+…+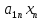 =
= ;
;
 +
+ +…+
+…+ =
= ;
;
 +
+ +…+
+…+ =
= .
В матричной форме система имеет вид:
A*X=B;
.
В матричной форме система имеет вид:
A*X=B;
 …
… матрица
коэф. системы
матрица
коэф. системы
 матрица – столбец
матрица – столбец
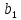 матрица-столбец
матрица-столбец
 …
… Х=
Х=
 переменных B=
переменных B=
 свободных членов
свободных членов
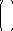

 …
…


Метод
Гаусса – метод последовательного
исключения переменных. Суть метода:
преобразовать исходную систему к
равносильной ей системе с треугольной
матрицей (прямой ход), из которой затем
последовательно записывают значения
всех переменных (обратный ход). Метод
Гаусса относится к точным методам, т.к.
погрешность самого метода равна нулю.
Из-за вычислительных погрешностей (при
округлении) получить точное решение
практически невозможно. Раздел А:
коэффициенты исходной системы и свободные
члены. Для исключения случайных ошибок
предусмотрен текущий контроль, для
этого используют столбец контроля сумм
( )
и столбец строчных сумм (S).
Контроль в прямом ходе: после того как
в раздел А внесены коэффициенты и
свободные члены исходной системы находят
контрольные суммы – складывают
коэффициенты и свободные члены по
строкам, результат вносят в раздел ∑.
Над контрольными суммами производят
те же операции, что и над свободными
членами. После выполнения каждого
преобразования находят строчную сумму
результатов и записывают ее в столбец
S(
)
и столбец строчных сумм (S).
Контроль в прямом ходе: после того как
в раздел А внесены коэффициенты и
свободные члены исходной системы находят
контрольные суммы – складывают
коэффициенты и свободные члены по
строкам, результат вносят в раздел ∑.
Над контрольными суммами производят
те же операции, что и над свободными
членами. После выполнения каждого
преобразования находят строчную сумму
результатов и записывают ее в столбец
S( ).
При отсутствии случайных ошибок числа
в столбцах ∑ и S
должны практически совпадать. Пусть b
– вычисляемый элемент нового раздела,
a
– соответствующий элемент предыдущего
раздела,
).
При отсутствии случайных ошибок числа
в столбцах ∑ и S
должны практически совпадать. Пусть b
– вычисляемый элемент нового раздела,
a
– соответствующий элемент предыдущего
раздела,
 - горизонтальная проекция элемента b,
- горизонтальная проекция элемента b,
 - вертикальная проекция элемента b.
Тогда b=a-
- вертикальная проекция элемента b.
Тогда b=a- .
Контроль в обратном ходе раздел В: в
столбце свободных членов получают
значения переменных, числа в столбце ∑
должны быть ровно на единицу больше
самих переменных. Значения в столбце ∑
можно получить, если при вычислении
переменных заменить свободные члены и
значения уже найденных переменных на
соответствующие числа из столбца ∑.
Вычислим погрешность: для этого подставим
найденные значения в исходную систему
и найдем разности между полученными
значениями и свободными членами
полученной системы. Эти разности
называются невязками.
.
Контроль в обратном ходе раздел В: в
столбце свободных членов получают
значения переменных, числа в столбце ∑
должны быть ровно на единицу больше
самих переменных. Значения в столбце ∑
можно получить, если при вычислении
переменных заменить свободные члены и
значения уже найденных переменных на
соответствующие числа из столбца ∑.
Вычислим погрешность: для этого подставим
найденные значения в исходную систему
и найдем разности между полученными
значениями и свободными членами
полученной системы. Эти разности
называются невязками.
