
- •Новосибирский Государственный Технический Университет ю.А. Гостеев
- •Часть 1
- •Юрий Анатольевич Гостеев гидравлика и газодинамика
- •Часть 1
- •Учебное пособие
- •630092, Г. Новосибирск, пр. К. Маркса, 20
- •Оглавление
- •Введение
- •1. Основные свойства жидкостей и газов. Гидростатика
- •1.1. Физические свойства и физические модели жидкостей и газов Капельные жидкости и газы
- •Силы, действующие в жидкости
- •Основные свойства капельных жидкостей
- •Плотность некоторых капельных жидкостей и газов
- •Динамическая вязкость жидкостей и газов
- •Физические модели жидкостей и газов
- •1.2. Гидростатика. Абсолютный и относительный покой жидкостей и газов
- •Свойства гидростатического давления
- •Основное уравнение гидростатики
- •Дифференциальные уравнения равновесия жидкости
- •Равновесие газов. Стандартная атмосфера
- •Силы давления жидкости на поверхности тел
- •2. Уравнения гидродинамики и их интегрирование
- •2.1. Кинематика потоков жидкости. Уравнение сохранения массы Основные понятия кинематики жидкости
- •Уравнение неразрывности
- •Расход и средняя скорость
- •2.2. Уравнения движения идеальной жидкости. Интеграл Бернулли. Потенциальное движение Вывод уравнений движения
- •Уравнение Бернулли
- •Примеры применения интеграла Бернулли
- •Безвихревое (потенциальное) движение жидкости
- •2.3. Уравнения движения вязкой жидкости. Обобщенный интеграл Бернулли Уравнения и режимы движения вязкой жидкости
- •Некоторые решения уравнений Навье–Стокса
- •Интеграл Бернулли для потока весомой несжимаемой вязкой жидкости
- •3. Основы гидравлики
- •3.1. Гидравлические потери На распределенных и местных сопротивлениях Разделение гидравлических потерь
- •Потери напора по длине трубы
- •Потери напора на местных гидравлических сопротивлениях
- •3.2. Гидравлический расчет трубопроводов
- •Простой трубопровод постоянного сечения
- •Соединения простых трубопроводов
- •Расчет сложного трубопровода
- •Расчет газопроводов
- •Работа насоса на гидросистему
- •4. Истечение жидкости из отверстий и насадков. Нестационарные явления
- •4.1. Истечение жидкости из отверстий и насадков
- •Истечение из отверстия в тонкой стенке
- •Истечение через насадки
- •4.2. Нестационарные явления при течении жидкости в трубах Неустановившееся течение вязкой жидкости в жестких трубах
- •Кавитация
- •Гидравлический удар
- •5. Пограничный слой. Обтекание тел
- •5.1. Основы теории пограничного слоя Понятие о пограничном слое
- •Уравнения двумерного пограничного слоя
- •Течение Блазиуса
- •5.2. Устойчивость и отрыв пограничного слоя
- •5.3. Интегральный метод расчета пограничного слоя
- •Ламинарный пограничный слой
- •Турбулентный пограничный слой
- •Библиографический список
4.1. Истечение жидкости из отверстий и насадков
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки при постоянном напоре. Будем интересоваться в основном скоростью истечения и расходом жидкости.
Истечение из отверстия в тонкой стенке
1. Истечение
в газовую среду.
Картина установившегося истечения
жидкости из сосуда через малое отверстие
показана на рис. 4.1. При истечении из
отверстия в тонкой стенке криволинейные
траектории частиц жидкости сохраняют
свою форму и за пределами отверстия,
т. е.
после выхода из отверстия сечение струи
уменьшается и достигает минимальных
значений на расстоянии равном
![]() (
(![]() – диаметр отверстия).
Таким образом,
в сечении В-В
будет находиться как называемое сжатое
сечение струи жидкости.
– диаметр отверстия).
Таким образом,
в сечении В-В
будет находиться как называемое сжатое
сечение струи жидкости.
Отношение
площади сечения струи к площади отверстия
называется коэффициентом
сжатия
![]() ,
,
![]() , (4.1)
, (4.1)
где
![]() – площадь отверстия,
– площадь отверстия,
![]() – площадь сжатого сечения струи.
– площадь сжатого сечения струи.
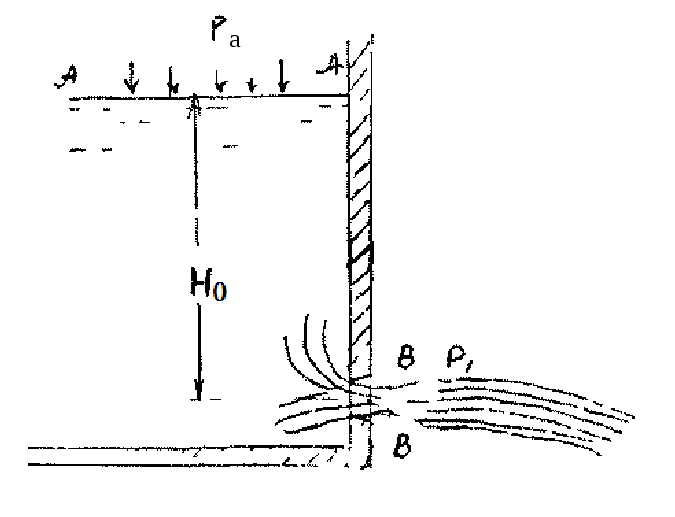
Рис. 4.1. Схема истечения жидкости в газовую среду
Запишем уравнение Бернулли для двух сечений А-А и В-В:
![]() ,
,
где
![]() – коэффициент сопротивления отверстия.
Поскольку
величина скоростного напора на свободной
поверхности жидкости (сечение А-А)
мала из-за малости скорости, ее величиной
можно пренебречь.
Тогда
– коэффициент сопротивления отверстия.
Поскольку
величина скоростного напора на свободной
поверхности жидкости (сечение А-А)
мала из-за малости скорости, ее величиной
можно пренебречь.
Тогда
![]() ,
,
где
![]() – расчетный напор. Следовательно,
скорость в сжатом сечении струи
– расчетный напор. Следовательно,
скорость в сжатом сечении струи
![]() .
(4.2)
.
(4.2)
Сомножитель
![]() в равенстве (4.2) носит название коэффициента
скорости.
в равенстве (4.2) носит название коэффициента
скорости.
Зная
скорость в сжатом сечении
![]() ,
определим расход жидкости:
,
определим расход жидкости:
![]() ,
(4.3)
,
(4.3)
где
![]() называется коэффициентом
расхода;
называется коэффициентом
расхода;
![]() – идеальной
скоростью истечения
[ср. с (2.23)].
– идеальной
скоростью истечения
[ср. с (2.23)].
2
 Рис. 4.2.
Об условии совершенного сжатия струи
Рис. 4.2.
Об условии совершенного сжатия струи![]() ,
,
![]() ,
т.е. не ближе тройного расстояния от
направляющих стенок (рис. 4.2), то линии
тока вблизи отверстия имеют одинаковую
кривизну и сжатие струи называется
совершенным.
,
т.е. не ближе тройного расстояния от
направляющих стенок (рис. 4.2), то линии
тока вблизи отверстия имеют одинаковую
кривизну и сжатие струи называется
совершенным.
В иных случаях близко расположенные стенки являются для струи направляющими элементами и ее сжатие будет несовершенным (не одинаковым со всех сторон). В тех случаях, когда сечение отверстия не круглое, сжатие струи будет неполным. При неполном и несовершенном сжатии струи наблюдается некоторое увеличение коэффициента расхода.
При
полном совершенном сжатии струи
коэффициент сжатия
![]() достигает 0.60…0.64. Величины коэффициентов
сжатия струи, коэффициента расхода
зависят от числа Рейнольдса
достигает 0.60…0.64. Величины коэффициентов
сжатия струи, коэффициента расхода
зависят от числа Рейнольдса
![]() (рис. 4.3): с возрастанием
(рис. 4.3): с возрастанием
![]() коэффициент скорости увеличивается, а
коэффициент сжатия струи убывает.
коэффициент скорости увеличивается, а
коэффициент сжатия струи убывает.
Величина коэффициента расхода измеряется простым замером фактического расхода жидкости через отверстие и сопоставлением его с теоретически вычисленным значением:
![]() .
.
Коэффициент сжатия струи измеряется по сжатому сечению струи. Коэффициент скорости определяется по траектории струи:
![]() ,
(4.4)
,
(4.4)
где
![]() и
и
![]() – вертикальная и горизонтальная
координаты оси струи.
– вертикальная и горизонтальная
координаты оси струи.

Рис. 4.3.
Зависимости
коэффициентов расхода,
скорости и
сжатия от
![]() для круглого
отверстия в
тонкой стенке
для круглого
отверстия в
тонкой стенке
Пример 4.1. Определить
коэффициенты расхода, скорости, сжатия
и сопротивления при истечении воды в
атмосферу через отверстие диаметром
![]() 10 мм
под напором
10 мм
под напором
![]() 2 м,
если расход
2 м,
если расход
![]() 0.294 л/с,
а координаты центра одного из сечений
струи
0.294 л/с,
а координаты центра одного из сечений
струи
![]() 2.3 м
и
2.3 м
и
![]() 1.2 м.
1.2 м.
Решение.
Площадь отверстия
![]() 7.85∙10–5 м2.
Тогда идеальная скорость истечения
7.85∙10–5 м2.
Тогда идеальная скорость истечения
![]() 6.26 м/с,
что соответствует числу Рейнольдса
6.26 м/с,
что соответствует числу Рейнольдса
![]() 6.26∙104;
коэффициент расхода
6.26∙104;
коэффициент расхода
![]() 0.598.
Коэффициент скорости согласно (4.4):
0.598.
Коэффициент скорости согласно (4.4):
![]() = 0.969. Следовательно, коэффициент
сжатия
= 0.969. Следовательно, коэффициент
сжатия
![]() = 0.617. Приняв коэффициент Кориолиса
= 0.617. Приняв коэффициент Кориолиса
![]() 1,
находим коэффициент сопротивления
1,
находим коэффициент сопротивления
![]()
![]() 0.032.
0.032.
В
области весьма малых
![]() (
(![]() 25)
можно пользоваться теоретической
формулой:
25)
можно пользоваться теоретической
формулой:
![]() .
.
Для маловязких
жидкостей (воды, бензина, керосина и
др.) можно принимать
![]() 0.64,
0.64,
![]() 0.97,
0.97,
![]() 0.62,
0.62,
![]() 0.065.
0.065.
2. Истечение через затопленное отверстие. Истечение через затопленное отверстие в тонкой стенке, т.е. под уровень жидкости, ничем существенным не отличается от истечения в газовую среду. В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.

Рис. 4.4. Истечение через затопленное отверстие
Пусть в резервуаре
имеется перегородка с отверстием, уровни
жидкости находятся на отметках
![]() и
и
![]() относительно плоскости сравнения,
проходящей через центр тяжести отверстия
(рис. 4.4). Запишем уравнение Бернулли
для свободных поверхностей жидкости
(сечение 0-0
и сечение 2-2),
где скорости считаем равными нулю. Учтем
при этом, что:
относительно плоскости сравнения,
проходящей через центр тяжести отверстия
(рис. 4.4). Запишем уравнение Бернулли
для свободных поверхностей жидкости
(сечение 0-0
и сечение 2-2),
где скорости считаем равными нулю. Учтем
при этом, что:
-
потери напора при истечении из отверстия в тонкой стенке равны
 ;
; -
потери на внезапное расширение струи от сжатого сечения до сечения резервуара равны
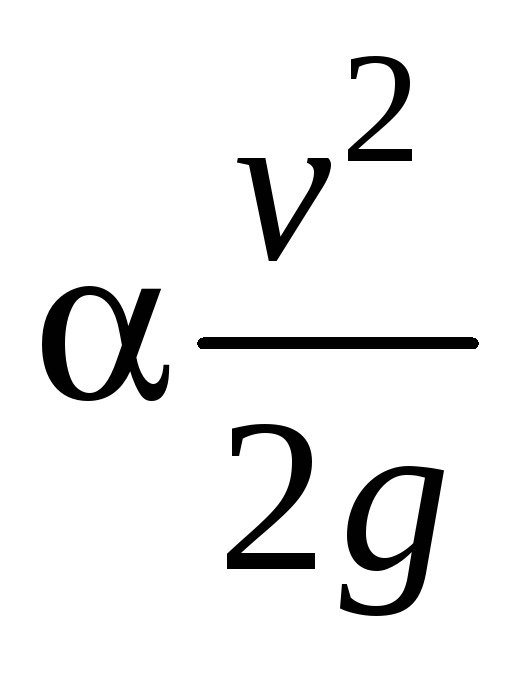 .
.
Тогда
![]() .
.
После преобразований получаем формулы
![]() ,
,
![]() ,
,
![]() ,
(4.5)
,
(4.5)
где расчетный напор есть разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход не зависят от высоты расположения отверстия.
