
- •Новосибирский Государственный Технический Университет ю.А. Гостеев
- •Часть 1
- •Юрий Анатольевич Гостеев гидравлика и газодинамика
- •Часть 1
- •Учебное пособие
- •630092, Г. Новосибирск, пр. К. Маркса, 20
- •Оглавление
- •Введение
- •1. Основные свойства жидкостей и газов. Гидростатика
- •1.1. Физические свойства и физические модели жидкостей и газов Капельные жидкости и газы
- •Силы, действующие в жидкости
- •Основные свойства капельных жидкостей
- •Плотность некоторых капельных жидкостей и газов
- •Динамическая вязкость жидкостей и газов
- •Физические модели жидкостей и газов
- •1.2. Гидростатика. Абсолютный и относительный покой жидкостей и газов
- •Свойства гидростатического давления
- •Основное уравнение гидростатики
- •Дифференциальные уравнения равновесия жидкости
- •Равновесие газов. Стандартная атмосфера
- •Силы давления жидкости на поверхности тел
- •2. Уравнения гидродинамики и их интегрирование
- •2.1. Кинематика потоков жидкости. Уравнение сохранения массы Основные понятия кинематики жидкости
- •Уравнение неразрывности
- •Расход и средняя скорость
- •2.2. Уравнения движения идеальной жидкости. Интеграл Бернулли. Потенциальное движение Вывод уравнений движения
- •Уравнение Бернулли
- •Примеры применения интеграла Бернулли
- •Безвихревое (потенциальное) движение жидкости
- •2.3. Уравнения движения вязкой жидкости. Обобщенный интеграл Бернулли Уравнения и режимы движения вязкой жидкости
- •Некоторые решения уравнений Навье–Стокса
- •Интеграл Бернулли для потока весомой несжимаемой вязкой жидкости
- •3. Основы гидравлики
- •3.1. Гидравлические потери На распределенных и местных сопротивлениях Разделение гидравлических потерь
- •Потери напора по длине трубы
- •Потери напора на местных гидравлических сопротивлениях
- •3.2. Гидравлический расчет трубопроводов
- •Простой трубопровод постоянного сечения
- •Соединения простых трубопроводов
- •Расчет сложного трубопровода
- •Расчет газопроводов
- •Работа насоса на гидросистему
- •4. Истечение жидкости из отверстий и насадков. Нестационарные явления
- •4.1. Истечение жидкости из отверстий и насадков
- •Истечение из отверстия в тонкой стенке
- •Истечение через насадки
- •4.2. Нестационарные явления при течении жидкости в трубах Неустановившееся течение вязкой жидкости в жестких трубах
- •Кавитация
- •Гидравлический удар
- •5. Пограничный слой. Обтекание тел
- •5.1. Основы теории пограничного слоя Понятие о пограничном слое
- •Уравнения двумерного пограничного слоя
- •Течение Блазиуса
- •5.2. Устойчивость и отрыв пограничного слоя
- •5.3. Интегральный метод расчета пограничного слоя
- •Ламинарный пограничный слой
- •Турбулентный пограничный слой
- •Библиографический список
Потери напора по длине трубы
В гидравлических расчетах распределенных потерь коэффициент сопротивления представляют в виде
![]() ,
(3.3)
,
(3.3)
где
![]() и
и
![]() – длина и внутренний диаметр трубы,
– длина и внутренний диаметр трубы,
![]() – безразмерный
коэффициент гидравлического трения,
определяемый в зависимости от режима
течения.
– безразмерный
коэффициент гидравлического трения,
определяемый в зависимости от режима
течения.
1. Потери напора по длине при ламинарном течении. Как показывают анализ (см. раздел 2.3) и опыты при ламинарном режиме движения жидкости в круглой трубе, осевая скорость в поперечном сечении распределена по параболе: у стенок трубы равна нулю и, плавно увеличиваясь, достигает максимума на оси потока. В этом случае силы сопротивления движению возникают в результате трения между слоями жидкости, т. е. зависят практически только от вязкости жидкости.
Из
формул (3.1) и (3.3) вытекает связь
![]() с потерями давления
с потерями давления
![]() ,
,
т. е.
![]() ,
,
где согласно (2.41), (2.42)
![]() . (3.4)
. (3.4)
Тогда
![]() ,
,
![]() .
(3.5)
.
(3.5)
Таким
образом, при ламинарном режиме течения
коэффициент гидравлического трения
обратно пропорционален числу Рейнольдса.
Закон
сопротивления (3.5) в круглой трубе
подтверждается результатами измерений
вплоть до чисел
![]() 2300.
2300.
С учетом (3.4) и (3.5) получаем следующее выражение для потерь напора по длине:
![]() . (3.6)
. (3.6)
Из (3.6) следует, что при ламинарном режиме потери напора пропорциональны средней скорости (расходу).
2
Рис. 3.1.
Зависимость потерь напора от скорости
течения
Экспериментально
подтверждается, что при турбулентном
режиме движении потери напора по длине
зависят от состояния стенок, ограничивающих
поток. Качественный вид зависимости
потерь напора
от скорости
![]() представлен на рис. 3.1. Видно,
что при скорости меньше критической
представлен на рис. 3.1. Видно,
что при скорости меньше критической
![]() потери
напора
прямо пропорциональны первой степени
скорости (на графике участок 0–1).
После перехода от ламинарного режима
к турбулентному потери напора растут
пропорционально скорости в степени,
большей единицы (участок 2–3).
потери
напора
прямо пропорциональны первой степени
скорости (на графике участок 0–1).
После перехода от ламинарного режима
к турбулентному потери напора растут
пропорционально скорости в степени,
большей единицы (участок 2–3).
Потери напора на трение по длине при турбулентном установившемся равномерном движении жидкости в трубах могут быть рассчитаны по зависимости
![]() (3.7)
(3.7)
(формула
Дарси–Вейсбаха),
причем коэффициент трения
![]() в общем случае зависит от числа
в общем случае зависит от числа
![]() и относительной шероховатости стенок
трубы
и относительной шероховатости стенок
трубы
![]() ,
где
,
где
![]() – средняя высота бугорков шероховатости.
– средняя высота бугорков шероховатости.
В
случае движения жидкости по трубам
некруглого поперечного сечения, имеющим
гидравлический диаметр
![]() (
(![]() и
и
![]() – площадь и периметр сечения), для
оценки потерь можно пользоваться
формулой (3.7), где вместо
– площадь и периметр сечения), для
оценки потерь можно пользоваться
формулой (3.7), где вместо
![]() используется
используется
![]() .
.
Если
шероховатость трубы не влияет на
сопротивление, то трубу называют
гидравлически
гладкой.
В этом случае
![]() и для расчетов пригодна формула Конакова:
и для расчетов пригодна формула Конакова:
![]() ,
(3.8)
,
(3.8)
где
![]() (1…2)
106.
(1…2)
106.
Сравнение
(3.5) и (3.8) показывает, что с увеличением
![]() коэффициент
коэффициент
![]() уменьшается менее значительно, чем
уменьшается менее значительно, чем
![]() ,
что связано с гораздо меньшим влиянием
вязкости на сопротивление в турбулентном
потоке. Основную роль в образовании
потерь при турбулентном течении играют
перемешивание и рассеивание кинетической
энергии завихренных частиц.
,
что связано с гораздо меньшим влиянием
вязкости на сопротивление в турбулентном
потоке. Основную роль в образовании
потерь при турбулентном течении играют
перемешивание и рассеивание кинетической
энергии завихренных частиц.
Для расчета сопротивления шероховатых труб можно использовать эмпирические зависимости, полученные в опытах Никурадзе (рис. 3.2), или универсальную формулу Альтшуля:
![]() , (3.9)
, (3.9)
где
![]() – эквивалентная абсолютная шероховатость
стенок трубы. Характерные значения
– эквивалентная абсолютная шероховатость
стенок трубы. Характерные значения
![]() (в мм) для труб из различных материалов
приведены ниже.
(в мм) для труб из различных материалов
приведены ниже.
Стекло 0
Трубы, тянутые из латуни, свинца, меди 0…0.002
Высококачественные бесшовные стальные трубы 0.06…0.2
Стальные трубы 0.1…0.5
Чугунные асфальтированные трубы 0.1…0.2
Чугунные трубы 0.2…1.0
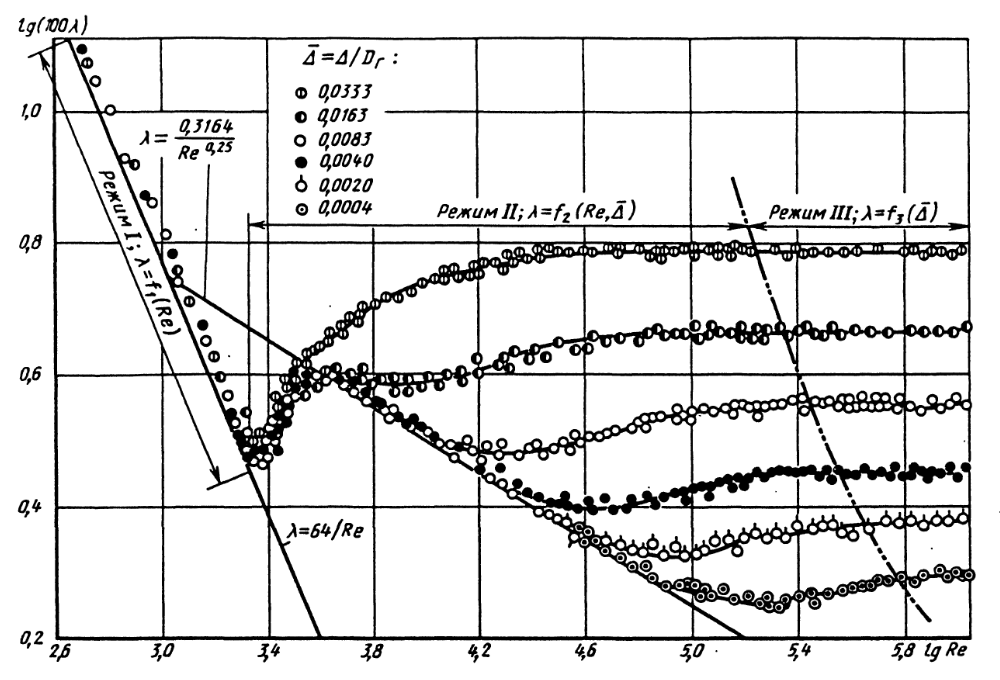
Рис. 3.2. Диаграмма Никурадзе
