2.5. Асимптоты

а) Вертикальная асимптота.

Если выполнено хотя бы одно из условий

,

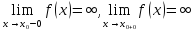
то прямую x=x0 называют вертикальной асимптотой графика функции y=f(x) .

Например, прямая x=0 - вертикальная асимптота графиков y=1/x , y=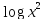

б) Невертикальные асимптоты.

Прямую y=kx+b

называют асимптотой (невертикальной асимптотой) графика функции y=f(x) при x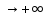, если

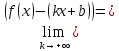0

Если k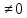 , асимптоту называют наклонной, а если k=0, то асимптоту y=b называют горизонтальной.

2.6. Возрастание и убывание функции

а) Критерий возрастания (убывания) дифференцируемой функции на интервале.

Теорема 1.

Для того чтобы дифференцируемая на интервале(a,b) функция y=f(x) была возрастающей на этом интервале необходимо и достаточно, чтобы выполнялось условие

f’(x) при всех x .

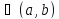Аналогично, условие

f’(x)при все x .

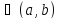является необходимым и достаточным для убывания дифференцируемой функции y=f(x) на интервале (a,b).

Доказательство (для случая, возрастающей функции).

Необходимость.

Пусть x0 - произвольная точка интервала(a,b). Из определения возрастающей функции следует, что

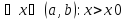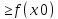
, f(x)

, f(x)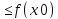

Следовательно, если 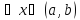и x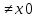 , то выполняется неравенство

(1)

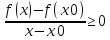
Т.к. левая часть (1) имеет при xпредел, равный f’(x) , то из неравенства (1) по свойству сохранения знака некоторого неравенства при предельном переходе получаем

f’(x0) 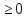для любого x0

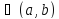
Достаточность.

Пусть выполняется условие f’(x) 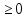при всех x 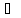(a,b) и пусть x1, x2- произвольные точки интервала(a,b) , причем x1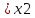. Применяя к функции f(x) на отрезке 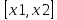теорему Лагранжа, получаем

f(x1)-f(x2)=f’(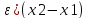

где f’(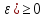, так как .

Отсюда следует, что ..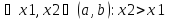

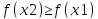Это означает, что функция является возрастающей на интервале(a,b) .

Теорема 1 доказана.

б) Достаточное условие строгого возрастания (убывания функции).

Теорема 2.

Если для всех x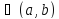 выполняется условие

f’(x)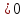 ,то функция f(x) строго возрастает на интервале(a,b) , а если для всех x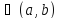 справедливо неравенство

f’(x)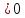,то функция f(x) строго убывает на интервале (a,b).

Доказательство (для функции строго возрастающей).

Пусть x1 и x2- произвольные точки интервала (a,b) такие что x1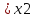. По теореме Лагранжа

. f(x1)-f(x2)=f’(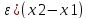, где ,

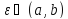Отсюда и из условияf’(x)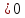 следует, что f(x2)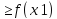. Это означает, что функция f(x) строго возрастает на интервале(a,b).

Теорема 2 доказана.

Теорема 3.

Если f’(x0)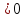, то функция f(x) строго возрастает в точке x0 , а если , f’(x0) то функция строго убывает в точкеx0 .

Доказательство.

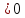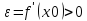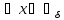Пусть например f’(x0) . Из определения производной следует, что по заданному числу можно найти такое, что для всех (x0) выполняется условие , 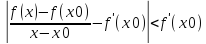откуда следует утверждение

Теорема 3 доказана.

2.7. Нули функций

Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем) функции.

2.8. Периодическая функция

Периодическая функция. Функция f ( x ) - периодическая, если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f(x + T) =f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.