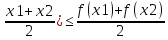- •Глава 1. Развитие понятия функции.
- •Глава 2. Основные свойства функции.
- •2.1. Четные и нечетные функции
- •2.2. Монотонность функции
- •2.3. Экстремумы функций
- •2.4. Выпуклость функций
- •2.5. Асимптоты
- •2.7. Нули функций
- •2.8. Периодическая функция
- •Глава 4. Построение графиков функций.
- •Глава 5. Примеры задач
- •Глава 6. Задачи:
Глава 2. Основные свойства функции.
Умение изображать геометрически функциональные зависимости, заданные
формулами, особенно важно для успешного усвоения курса высшей математики.
Как известно, функциональной зависимостью называют закон, по которому каждому
значению величины х из некоторого множества чисел, называемого областью
определения функции, ставится в соответствие одно вполне определенное
значение величины у; совокупность значений, которые принимает зависимая
переменная у, называется областью изменения функции.
Независимую переменную х называют также аргументом функции. Число у,
соответствующее числу х, называют значением функции f в точке х и обозначают
f(x).
Функцию можно задать тремя способами: аналитический, табличный, графический.
Аналитический – с помощью формул.
Табличный – с помощью таблиц, где можно указать значения функции, однако
лишь для конечного набора значений аргумента.
Графический способ задания функции очень удобен: он дает возможность
наглядно представить свойства функции.
Виды функций (четные, нечетные, общего вида, периодические функции).
Рассмотрим функции, области определения которых симметричны относительно
начала координат, то есть для любого х из области определения число (-х)
также принадлежит области определения. Среди таких функций выделяют четные и
нечетные.
2.1. Четные и нечетные функции
Функция f называется четной, если для любого х из ее
области определения f(-x)=f(x).
График четной функции симметричен относительно оси ординат.
Функция f называется нечетной, если для любого х из
ее области определения f(-x)=-f(x).
2.2. Монотонность функции
Функцию f
называют возрастающей на множестве
(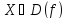 где-
D(f) область
определения функции f ),
если для любых точек x1
где-
D(f) область
определения функции f ),
если для любых точек x1 X и x2
X и x2 таких,
что x1
таких,
что x1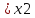 выполняется неравенство f(x1)
выполняется неравенство f(x1)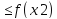 . Если это неравенство является строгим
f(x1)
. Если это неравенство является строгим
f(x1)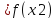 , то функцию f называют
строго возрастающей на множествеX
.
, то функцию f называют
строго возрастающей на множествеX
.
Таким образом, функция называется:
a) возрастающей на множестве , если X
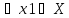
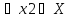 ,
x1
,
x1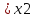
![]() f(x1)
f(x1) f(x2)
f(x2)
строго возрастающей на множестве , Xесли
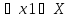
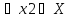 ,
x1
,
x1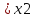
![]() f(x1)
f(x1)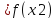
б) убывающей на множестве , если X
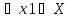
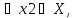 x1
x1
![]() f(x1)
f(x1)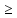 f(x2)
f(x2)
строго убывающей на множестве , если X
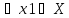
 , x1
, x1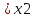
![]() f(x1)
f(x1)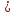 f(x2)
f(x2)
Убывающие и возрастающие функции объединяют названием монотонные, а строго возрастающие и строго убывающие - названием строго монотонные.
Будем говорить,
что функция f(x)
строго возрастает в точке x0
, если существует такое
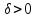 ,
что
,
что
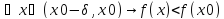
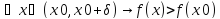
Аналогично
f(x) строго
убывает в точке x0 , если
существует
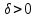 такое, что
такое, что
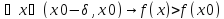
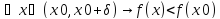
2.3. Экстремумы функций
Пусть
существует число
 такое, что функция f(x)
определена в
такое, что функция f(x)
определена в
 - окрестности точки x0 ,
т.е. на множестве
- окрестности точки x0 ,
т.е. на множестве
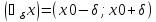 , и пусть для всех x
, и пусть для всех x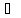
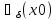 выполняется
неравенство f(x)
выполняется
неравенство f(x)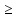 f(x0)
f(x0)
Тогда говорят, что функция f(x) имеет в точке x0 локальный минимум.
Аналогично,
если существует число
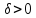 такое, что для всех x
такое, что для всех x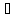
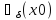 выполняется неравенство f(x)
выполняется неравенство f(x)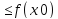 ,
,
то говорят, что функция f(x) имеет в точке x0 локальный максимум.
Локальный min и max объединяются общим термином локальный экстремум.
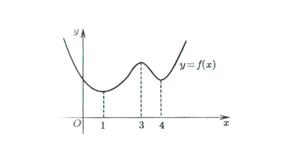
На рисунке функция y=f(x) имеет локальные экстремумы, а именно минимумы при x=1 и x=4 и максимум при x=3 .
2.4. Выпуклость функций
а) График функции y=f(x) называется выпуклым в интервале (a,b), если он расположен ниже касательной, проведенной в любой точке этого интервала.

График функции y=f(x) называется вогнутым в интервале (a,b) , если он расположен выше касательной, проведенной в любой точке этого интервала.
б) Непрерывная
функция y=f(x)
называется выпуклой на отрезке
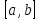 , если для любых точек x1
и x2 отрезка
, если для любых точек x1
и x2 отрезка
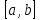 выполняется неравенство
выполняется неравенство
f(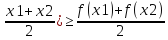
Аналогично,
функция y=f(x)
называется вогнутой на отрезке , если для любых точек x1
и x2 отрезка
, если для любых точек x1
и x2 отрезка
 выполняется неравенство
выполняется неравенство
f(