4.1.3. Решение системы линейных алгебраических уравнений решающим блоком Given…Find ( ).

Данный способ является приближённым , который реализуется несколькими методами, основными из которых являются линейные (Linear) и нелинейные методы (Nolinear), например, такие как метод сопряжённых градиентов, метод Ньютона и другие [ ].

Вычислительный блок Given…Find позволяет решать системы до 200 алгебраических уравнений.

В отличие от решения с помощью функции lsolve в блоке Given….Find(X) должно присутствовать начальное приближение для неизвестных. Начальное приближение присваивается неизвестным уравнений перед записью оператора Given(задано). Это приближение может быть введено непосредсвенным присвоением значений неизвестным (рис.4.2,а), либо, используя переменную диапазона

(см. раздел «Множества»). Второй способ (рис.4.2,б) предпочтительней при большой размерности системы уравнений, т.к. вектор начальных значений создаётся автоматически.

Таким образом, для решения системы линейных уравнений с помощью решающего блока Given….Find(X) необходимо:

- присвоить начальное приближение неизвестным системы;

- напечатать оператор Given;

- создать матрицу коэффициентов и вектор правых частей системы уравнений;

- напечатать Find(var1, var2,…)=(равно), где var1,var2,….- неизвестные системы уравнений и просмотреть результат решения.

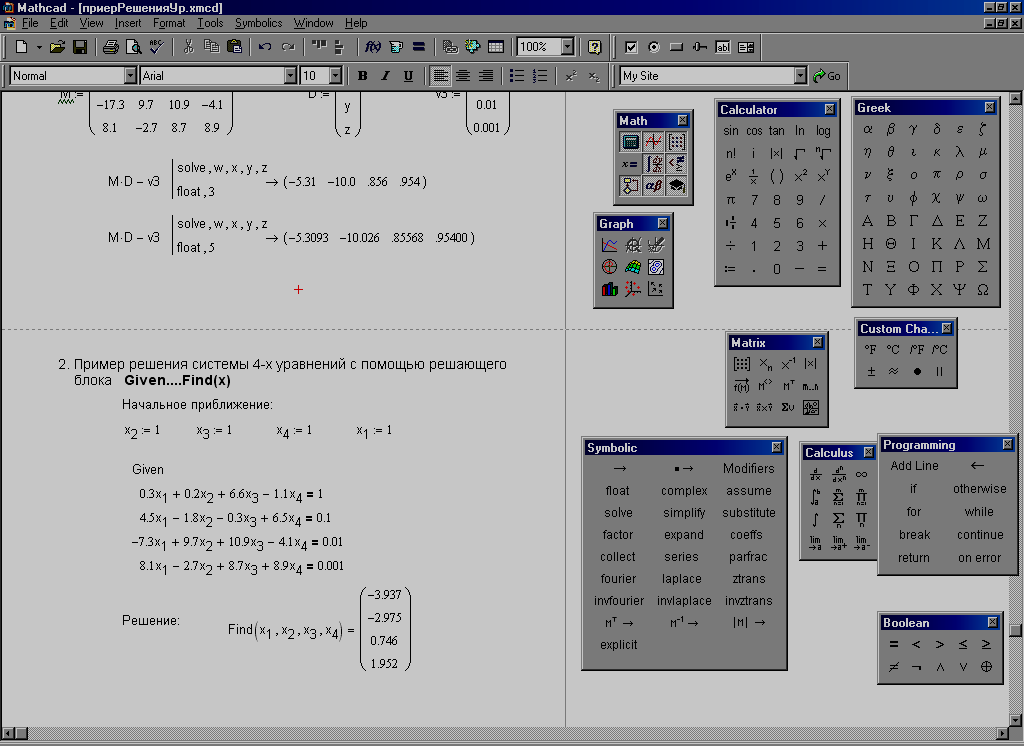
Рис.4.2, а.

Рис. 4.2, б.

Примечание:

1. В решающем блоке Given…Find уравнения записываются в любой общепринятой форме, в том числе в матричной, например, как показано на рис.4.2 а,б.

2. При записи системы уравнений в левая часть уравнений отделяется от правой знаком эквивалентности (выделенное =), который вставляется с панели Boolean мышью или может быть напечатан [Ctrl]=(равно) набором на клавиатуре.

3. Внутри блока не должно быть других вычисляемых выражений.

4. Функция Find может быть вставлена в рабочий лист из окна Insert Funrtion(вставка функции). Для этого в окне Category Function нужно выделить опцию Solving, а затем в окне Funrtion Name(имя функции) выделить функцию Find. После нажатия кнопки Insert(вставить) на месте курсора отобразится шаблон этой функции.

5. В отличие от функции lsolve в блоке Given…Find Given…Find должно присутствовать начальное приближение для всех неизвестных.

Рис. 4.3. Решение системы уравнений при произвольной форме записи системы алгебраических уравнений.

4.2. Решение систем нелинейных алгебраических уравнений

1. Решение с помощью вычислительного блока Given…Find.

Наиболее распространённым методом решения нелинейных алгебраических уравнений в MathCad является решение с помощью вычислительного блока Given…Find( ). Данный вычислительный блок реализует решение методом последовательных приближений, поэтому необходимо задавать начальное приближение для всех неизвестных системы уравнений. Последовательность создания рабочего листа следующая:

- присвоить начальное приближение – некоторое численное значение, неизвестным уравнений, например, напечатать: х₁:=а₁ х₂:= а₂… х_n:=а_n, где x_i (i=1,…,n) - имена неизвестных , a_i (i=1,…,n) –заданные числа, n – число уравнений;

- напечатать оператор Given;

- ввести заданные уравнения (напомним, что знак равенства вводится нажатием совокупности клавиш Сtrl+=(равно) или щелчком мыши на панели Boolean);

- напечатать vec := Find(x₁, x₂,…, x_n), где vec - имя матрицы-столбца неизвестных;

- напечатать vec= (равно) для вывода результатов решения уравнений и нажать клавишу Enter.

Рис. 4.6. Пример решения системы нелинейных алгебраических уравнений.