29. Уравнения касательной и нормали к кривой

Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x₀, y₀), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy.

Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x₀), то получаем уравнение y= f'(x₀)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x₀, y₀). Поэтому ее координаты должны удовлетворять уравнению касательной: y₀= f'(x₀)·x₀ + b. Отсюда b=y₀– f'(x₀)·x₀.

Таким образом, получаем уравнение касательной y= f'(x₀)·x +y₀ – f'(x₀)·x₀ или

y = f '(x0)·(x – x0) + f(x0)

Если касательная, проходящая через точку М(x₀,y₀) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x₀.

Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.

Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.

Из определения нормали следует, что ее угловой коэффициент k_n связан с угловым коэффициентом касательной k равенством:

.

Учитывая, что нормаль также как и касательная проходит через точку M(x₀, y₀), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:

Ясно, что если касательная параллельна оси Ox, т.е.f'(x₀) = 0 и ее уравнение имеет вид y= y₀, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x₀.

30) Основные правила дифференцирования. Сумма.

Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х₀ обозначаются для краткости так: u(х₀) = u, v(х₀) = v, u'(х₀) = u', v'(х₀)=v`. Если функции u и v дифференцируемы в точке х₀, то их сумма дифференцируема в этой точке и (u+v)' = u' + v'. Коротко говорят: производная суммы равна сумме производных.     1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х₀+Δx)+ v(х₀+Δx) – (u(х₀)+v(х₀)) = (u(х₀+Δx)-u(х₀)) + (v(х₀+Δx)-v(х₀)) = Δu + Δv 2)

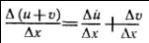
3) Функции u и v дифференцируемы в точке х₀, т. е. при Δх→0 Тогда при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’

Лемма. Если функция f дифференцируема в точке х₀, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е. f(х₀ + Δх)→f (х₀) при Δx→0. Действительно, при Δх→0, так как Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х₀ + Δx)→f (х₀) при Δх→0.

31. Производные шести тригонометрических функций и, соответственно, шести обратных тригонометрических функций определяются следующими формулами (рядом указана область определения каждой функции): В приведенных ниже примерах мы предполагаем, что читатель (или если кто предпочитает - "пользователь") знаком с основными тригонометрическими формулами.

) Производные тригонометрических функций. Формула производной синуса.

Докажем, что функция синус имеет производную в любой точке u (sin x)’ = cos x.

Применяя формулу находим

Для вывода формулы достаточно показать, что: при Δx→0. Опираясь на эти утверждения, можно получить формулу (1). Действительно, при Δx→0 Утверждения а) и б), на которые мы опирались выше, имеют наглядный геометрический смысл. 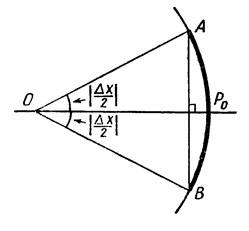а) Отложим на единичной окружности от точки Р₀ в обе стороны дуги Р₀А и Р₀В длиной |Δx|/2 (рис. сверху) Тогда длина дуги АВ равна |Δx|, а длина хорды AВ равна 2|sin (Δx/2)|. При малых |Δx| длина хорды АВ практически не отличается от длины стягиваемой ею дуги АВ. (Этим фактом вы уже пользовались в курсе геометрии при выводе формулы длины окружности. Действительно, при больших n верно, как известно, приближенное равенство Р_n≈С, где Р_n — периметр правильного вписанного n-угольника, а С — длина окружности. Значит, длина стороны такого многоугольника приближенно равна длине дуги, которую эта сторона стягивает.) Следовательно,

б) Заметим, что длина хорды АВ меньше длины дуги АВ, т. е.

Воспользовавшись формулой разности косинусов и этим неравенством, находим:

Но |Δx|/2→0 при Δx→0. Поэтому при Δx→0.