
- •Основы финансовых вычислений
- •Для всех специальностей Оглавление
- •Основы финансовых вычислений
- •1. Время как фактор стоимости
- •2. Операции наращения и дисконтирования
- •3. Простые проценты
- •3.1. Годовая процентная ставка и годовая учетная ставка
- •3.2. Алгоритм схемы простых процентов
- •3.3. Расчёт процентов при изменяющейся сумме вклада на счёте
- •3.4. Наращение по схеме простых процентов при переменной ставке
- •3.5. Наращение с капитализацией (реинвестированием) процентов
- •3.6. Факторный учёт векселя
- •3.7. Определение срока ссуды и величины ставки
- •3.8. Вычисление средних значений
- •3.9. Замена платежей и их консолидация
- •4. Сложные проценты
- •4.1. Наращение сложных процентов
- •4.2. Смешанная схема процентов
- •4.3. Внутригодовые процентные начисления
- •4.4. Эффективная годовая процентная ставка
- •4.5. Дисконтирование по сложной процентной ставке
- •4.6. Сложная учётная ставка
- •4.7. Эффективная учётная ставка
- •4.8. Наращение сложными процентами по учётной ставке
- •4.9. Замена платежей и сроков их выплат
- •5. Эквивалентность простых и сложных ставок
- •6. Непрерывное наращение и дисконтирование
- •6. Денежные потоки
- •6.1. Виды денежных потоков и задачи их анализа
- •6.2. Аннуитет (финансовая рента)
- •6.3. Оценка аннуитета
- •6.3.1. Прямая задача: наращенный денежный поток
- •6.3.2. Обратная задача: дисконтированный денежный поток
- •6.3.3. Бессрочный аннуитет (вечная рента)
3. Простые проценты
3.1. Годовая процентная ставка и годовая учетная ставка
За
единицу измерения промежутка времени
выбирается интервал времени в 1 год и
выбираются годовые ставки
 (нижний индекс «1» не указывается). Далее
предполагают, что
(нижний индекс «1» не указывается). Далее
предполагают, что

 ,
,
тде
 обозначение
интервала времени в 1 год, измеренного
в единицах времени: год = 12 месяцев = 2
полугодия = 4 квартала = 365 (366) дней.
Интервал
обозначение
интервала времени в 1 год, измеренного
в единицах времени: год = 12 месяцев = 2
полугодия = 4 квартала = 365 (366) дней.
Интервал
 измеряется в одноименных единицах.
Поэтому отношение
измеряется в одноименных единицах.
Поэтому отношение
 безразмерное и обычно выражает число
лет и может быть целым, дробным или
десятичным числом. В формулах годовые
ставки рассматриваются как безразмерные
коэффициенты. Например, если задана
годовая ставка
безразмерное и обычно выражает число
лет и может быть целым, дробным или
десятичным числом. В формулах годовые
ставки рассматриваются как безразмерные
коэффициенты. Например, если задана
годовая ставка
 ,
то в формулах она будет встречаться как
,
то в формулах она будет встречаться как
 .
.
Замечание.
1. Относительно продолжительности финансовой операции договорились, что день выдачи и день погашения ссуды считать за один день.
2. По продолжительности года проценты подразделяются:
-
на точные проценты, когда

 ;
; -
обыкновенные проценты:
 .
.
3.
В результате используют три схемы
расчёта отношения
 :
:
а) схема 360/360 , называемая обыкновенными процентами (Германия, Дания, Швеция);
в) схема 365/360, применяемая, например, в Бельгии, Франции;
г) схема 365/365, называемая точными процентами (Англия, США).
3.2. Алгоритм схемы простых процентов
А)
алгоритм с применение годовой процентной
ставки
 .
.
В формулу

подставим

получим

 .
.
Решив
последнее равенство относительно
 ,
получим формулу
наращения по схеме простых процентов
с применением годовой ставки процентов:
,
получим формулу
наращения по схеме простых процентов
с применением годовой ставки процентов:
 .
(1)
.
(1)
Разрешив
формулу (1) относительно
 ,
получим формулу математического
дисконтирования по схеме простых
процентов:
,
получим формулу математического
дисконтирования по схеме простых
процентов:
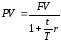 .
(2)
.
(2)
Проценты равны
 .
(3)
.
(3)
Замечание.
Формулу (3) можно записать в виде
 ,
,
где
 дивизор,
дивизор,
 процентное число.
процентное число.
В)
алгоритм с применением годовой учетной
ставки
 .
.
В формулу

подставим

и получим равенство

 ,
,
которое
разрешим относительно
 и получим формулу
наращения по схеме простых процентов
с применением учетной ставки:
и получим формулу
наращения по схеме простых процентов
с применением учетной ставки:
 .
(4)
.
(4)
Разрешив
равенство (4) относительно
 ,
получим формулу
дисконтирования по схеме простых
процентов с применением процентной
учетной ставки:
,
получим формулу
дисконтирования по схеме простых
процентов с применением процентной
учетной ставки:
 .
(5)
.
(5)
В
формулах (4) и (5) должно быть
 ,
что накладывает ограничение на период
кредитования
,
что накладывает ограничение на период
кредитования
 при заданном значении учетной ставки
при заданном значении учетной ставки
 ,
а именно:
,
а именно:
 .
(6)
.
(6)
т. е. учётная ставка более жёстко отражает фактор времени.
Замечание.
1.
Условимся в дальнейших формулах вместо
 писать просто
писать просто
 .
Например, формулу (1) теперь запишем в
виде:
.
Например, формулу (1) теперь запишем в
виде:
 .
.
2. Расчеты по формуле (5) называют банковским дисконтированием (банковским учётом), поскольку они применяются банками при операции учёта векселей. Вексель – письменное безусловное обязательство векселедателя (заёмщика) уплатить в установленный срок определённую сумму предъявителю векселя или лицу, указанному в векселе.
