1.6.3. Совместное течение двух несмешивающихся жидкостей в плоском канале (стратифицированное течение)

Математический анализ восполняет краткость нашей жизни и несовершенство наших чувств. Он идет одной и той же дорогой в изучении всех явлений; он объясняет их одним языком, как бы для того, чтобы подчеркнуть единство и простоту устройства вселенной.

Фурье Жане Батист (1768-1830гг).

Экспериментально обнаружено, что при течении двух несмешивающихся жидкостей в канале ограниченного сечения маловязкая жидкость обволакивает высоковязкую, отделяет ее от стенок как показано на рис. 1.9. При этом затраты энергии на транспортировку значительно снижаются. Этот эффект используется при транспортировке нефти, путем добавления воды - как маловязкой жидкости. Кроме того, существует технологический процесс производства многослойных полимерных пленок из расплавов полимеров посредством плоскощелевой формующей головки. Таким образом, рассматриваемая задача имеет широкое приложение.

Схема течения и система координат показаны на рис. 1.10. Две несмешивающиеся жидкости различной вязкости и расходом движутся п од действием избыточного давления вдоль плоского канала. Ось х соответствует направлению течения. Начало декартовой системы координат поместим на поверхности соприкосновения двух жидкостей. Режим течения - ламинарный. Жидкости ньютоновские. Течение изотермическое, установившееся. Гидродинамическое влияние боковых стенок не учитываем. Требуется найти профили скоростей, расходы жидкостей и соотношение толщины слоев.

Течение описывается системой уравнений движения в декартовой системе координат

; ; ;

Здесь индексом 1 отмечены параметры верхнего слоя, а индексом 2 – нижнего.

Граничные условия задачи. Принимаем на поверхностях канала условия прилипания:

y=₁, ₁=0; y=-₂, ₂=0. (1.4)

На границе раздела жидкостей имеет место равенство скоростей

y=0, ₁=₂ (1.5)

и равенство (или непрерывность) касательных напряжений

y=0, . (1.6)

Проинтегрируем уравнения движения

, .

Из условия равенства касательных напряжений (1.6) следует

с₁=с₂.

Выполнив повторное интегрирование уравнений, имеем

, .

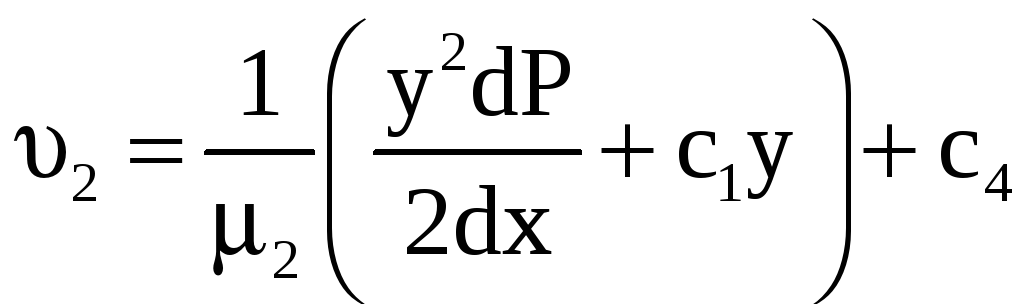Используем условие равенства скоростей на стыке жидкостей (1.5). Откуда имеем ₁=c₃; ₂=c_4. Следовательно с₃=с_4, При этом для распределения скоростей имеем

,

Из полученных выражений видно, что профили скорости описываются параболами.

Постоянные с₁ и с₃ найдем из условий прилипания жидкости к стенкам канала (1.4)

, .

Вычитая из первого равенства второе, находим постоянную с₁

.

После преобразований можем записать следующие выражения для постоянных:

, .

Профили скоростей в каждом из слоев описываются следующими выражениями:

,

.

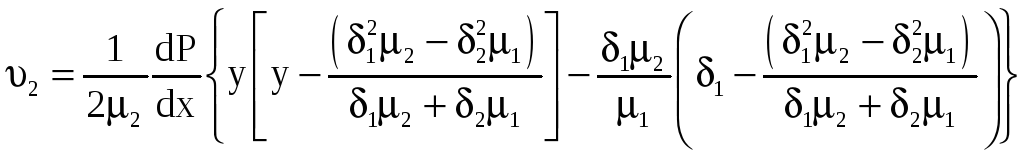Общий объемный расход Q равен сумме расходов жидкостей

Q=Q₁+Q₂,

где -расход верхнего слоя жидкости; , b – ширина щели.

Выполнив интегрирование, найдем

,

.

Из полученных выражений видно, что профили скоростей в слоях жидкостей зависят от соотношения их толщины и вязкости.

Аналогично может быть решена задача течения любого конечного числа слоев разнородных жидкостей.

Пример.

Посредством плоскощелевой головки формуется бикомпонентная полимерная пленка. Давление в головке 20 Мпа, протяженность губок фильеры 30 мм, толщины слоев различных полимеров 0,5 мм и 0,5 мм. Ширина формуемого полотна 1 м. Вязкость первого полимера 10² Па^.с, второго – 10³ Па^.с. Найти расходы полимеров.

Решение.

Используем расчетные формулы

,

.

Подставив численные значения, найдем

, .

Задачи.

1. Как изменятся расходы компонентов в условиях рассмотренного примера, если давление в головке увеличить в 2 раза?

2. Какому виду течения будет соответствовать решение задачи, если в расчетных формулах положить δ₁=-δ₂=δ, μ₁= μ₂= μ?