Соответственно, на валу второго ротора

.

Здесь .

Потребляемая мощность первым ротором . Вторым

Общая потребляемая мощность двумя роторами

(5)

Выделяющееся при перемешивании тепло, в результате диссипации, необходимо отводить охлаждающей водой, которая подается в рубашку камеры. Уравнение теплового баланса имеет вид N=GC(t_к – t_н), где G – расход воды, С- теплоемкость, t_к, t_н – конечная и начальная температура воды.

Исследуем пусковой период резиносмесителя. Пусть в начальный момент температура смеси соответствовала температуре охлаждающей жидкости. При включении привода резиносмесителя происходит диссипативный саморазогрев смеси за счет превращения механической энергии в тепловую. Мощность тепловыделения характеризуется N (см. формулу (6)). По истечении пускового периода температурное поле в системе стабилизируется. Представляет интерес найти температуру смеси в условиях переходного процесса и влияние на динамику условий охлаждения. Термическим сопротивлением ротора пренебрегаем. Учитываем только коэффициент теплоотдачи от наружной стенки ротора к охлаждающей жидкости.

Рассмотрим смеситель как реактор периодического действия. С учетом принятых допущений, уравнение теплового баланса имеет вид:

,

где - масса смеси и стенки камеры; - теплоемкость материала смеси и стенки камеры; S - площадь теплоотдающей поверхности смесительного канала; - коэффициент теплоотдачи.

Имеем дифференциальное уравнении 1-го порядка с разделяющимися переменными. Уравнение необходимо дополнить начальным условием: t=0, T=T_о.

Разделим переменные и проинтегрируем

.

Откуда имеем для температуры выражение

.

Численные значения мощности перемешивания и зависимость температуры от времени получены при помощи программы MathCad.

Приложение 3. Фрагмент выпускной бакалаврской работы Митиной Т.Н. на тему «Процесс грануляции сульфенамида».

Определение скорости вращения мешалки. Жидкость в реакторе представляет суспензию твердых частиц. Плотность частиц сульфенамида отличается от плотности сплошной фазы. Для предотвращения осаждения частиц служит мешалка. Восходящий поток жидкости поддерживает твердые частицы во взвешенном состоянии, препятствуя их осаждению[1]. Число оборотов n₀ может быть определено по уравнению [1]

Re_м = n₀d²/ = С₁Ar(d_r/d)^0,5 (D/d)^k , (1)

где Ar = (gd³_r /²_c)(/  критерий Архимеда,   разность плотностей фаз _сплотность сплошной фазы _скинематическая вязкость сплошной фазы d_r  диаметр частиц D/d  отношение диаметра сосуда к диаметру мешалки. Значения коэффициентов для лопастной мешалки c₁ 14,8 k 0

Уравнение (1) применимо при следующих значениях переменных Re_м = 5*10²– 1,3*10⁵; Ar = 2,4*10⁴ – 4,1*10¹¹; d_r/d = 2 *10^-4 – 10^-2 .

В критерий Рейнольдса входит вязкость суспензии. Вязкость находится по формуле [1, с.184]  _c 1+45 где _c  вязкость сплошной фазы (_c= 10^-3 Пас); - объемная концентрация частиц ( = 0,15). Следовательно,  = =10^-3_*(1+4,5_*0,15) = 1,675*10^-3 Па с.

В рассматриваемом случае условия перемешивания следующие:  1030 кг/м ³, _r = 1400 кг/м ³, _с= 10^-3 Па с; d_r= 70 мкм; d= 1,1 м.

Найдем число Архимеда

Ar =1,207

Находим критерий Рейнольдса по уравнению (1)

Re_м = 14,8 1,207(70*10^-6(10^0,5)/1,1)= 0,1425.

Откуда находим минимальное число оборотов мешалки, обеспечивающее гомогенизацию суспензии

n₀ =( Re_м d²  0.1425*1.67 (10^-3)  / ((1.1²) 1030) = 1.9 10^-7 об/с.

Проведенный расчет показывает, что суспензия достаточно устойчива, поскольку требуется весьма малая скорость вращения мешалки для поддержания частиц во взвешенном состоянии. Связано это с низкой скоростью осаждения частиц, которую характеризует критерий Архимеда.

В реальном аппарате скорость вращения мешалки n = 1 об/с. Следовательно, гомогенность суспензии обеспечена. Такая сравнительно высокая скорость мешалки обусловлена интенсификацией съема тепла со стенок аппарата и выравниванием по объему суспензии поля температур.

Передача тепла от стенки реактора к жидкости. Суспензия поступает в реактор при температуре 30С. Для подогрева суспензии в рубашку реактора подается пар под давлением 3 ат. Следовательно, температура внутренней стенки реактора составляет 133С.

Найдем тепловой поток от стенки реактора к жидкости. Имеет место теплопередача. Пар, конденсируясь в рубашке, отдает тепло наружной стенке реактора. Далее тепло путем теплопроводности передается к внутренней стенке реактора. От внутренней стенки тепло отдается жидкости. Принимаем коэффициент теплоотдачи при конденсации пара в рубашке: _п = 15000 Вт/м ² К. Термическое сопротивление стенки характеризуется:   46 Вт/м^.К,  = 0,016 м.

Таким образом, тепловой поток к жидкости от стенки Q составляет:

Q = FK(T_k-T),

где F – поверхность аппарата, K–коэффициент теплопередачи (К=(1/_п)^-1), T_k – температура конденсации пара, T –температура жидкости.

Определим коэффициент теплоотдачи. Согласно [2], для аппаратов с мешалками справедливо критериальное уравнение

Nu = 0.36Re^0.67Pr^0.33 (_cт)^0,14Г^-1 ,

где Re = nd_м² Nu = d_м Г=D/d_м; D – диаметр сосуда; n – частота вращения мешалки; d_м – диаметр мешалки; _ст – вязкость жидкости при температуре стенки;  вязкость при средней температуре жидкости. Отмечается, что эта формула справедлива для лопастных мешалок. Подобное уравнение приведено также в работе [3]

Nu = 0.36Re_м^0,67Pr^0.33, (2)

где Re_м = nd_м² Nu = D

Для расчета коэффициента теплоотдачи используем уравнение (2).

Примем среднюю температуру жидкости 60С При этой температуре вязкость жидкости (воды) =0,5*10^-3 Па с, соответственно Pr=3, =0,663 Вт/мК.

Вычислим критерий Рейнольдса

Re_м = nd_м²  (1_*1030_*1,1²)/ (0,5_*10^-3) = 2,49 *10⁶ .

Согласно (2) имеем для Нуссельта

Nu = 0,36(2,49_*10⁶)^0,67 3^0,33= 9981.

Откуда, учитывая D = 1,8 м, имеем

Nu/D = 0,57_*0,163_*9981/1,8 = 3675 Вт/м²К.

Находим коэффициент теплопередачи

К =  1456 Вт/ м ²К.

Имеем задачу нестационарного нагрева жидкости. Согласно уравнению нестационарного макроскопического баланса энергии для температуры жидкости можем записать дифференциальное уравнение [4]

сV dT/dt = KF(T_k-T), (3)

где c – теплоемкость жидкости;V – объем жидкости в аппарате; F – поверхность аппарата; Tk – температура конденсации пара; Т – температура жидкости; t - время.

Начальные условия для уравнения (3)

t = 0, Т = Т₀=30С. (4).

В уравнении (3) разделим переменные

dT/(T_k-T) = (KF/(cV))dt

и проинтегрируем с учетом (4)

(T_k-T)/(T_k-T₀) = exp[-KF t /(cV)]. (5).

Согласно (5)температура жидкости повышается экспоненциально.

Прогрев частиц в суспензии. Задача состоит в исследовании процесса прогревания твердых частиц сульфенамида. Интенсивность нестационарного прогрева частицы зависит от интенсивности подвода тепла со стороны окружающей жидкости. Для расчета интенсивности внешнего теплообмена частицы можно использовать уравнение Фросслинга[5]. Согласно этой теории коэффициент теплоотдачи не зависит от размеров частиц. Объясняется это тем, что скорость теплообмена контролируется турбулентными пульсациями, масштаб которых по порядку величины близок к толщине вязкого подслоя и не зависит от размеров обтекаемого тела. Таким образом, теория турбулентных пульсаций Ландау применима для частиц, размер которых больше 0,06-0,1 мм. В случае частиц меньшего размера, коэффициент теплоотдачи определяется скоростью относительного движения частиц в жидкости и увеличивается с уменьшением их диаметра.

Зная, что режим осаждения ламинарный, используем формулу Стокса для определения скорости осаждения:

V ==  9,87 10^-4 м/с

Найдем критерий Рейнольдса:

Re = = = 7,11*10^-2

Для определения коэффициента теплоотдачи на поверхности частицы используем критериальное уравнение[6]

Nu = 2+(0,4_*Re ^0,5+ 0,06_*Re^2/3) Pr^0,4.

Подставим численные значения

Nu = 2+[0,4(7.11_*10^-2)^0,5+0,06(7.11_*10^-2)^2/3*3^0,4 , Nu = 2,18.

Откуда _r = (Nu )d=2,18_* 0,57_*1,163/(70_*10^-6) = 20658 Вт/м² К.

Видно, что интенсивность теплообмена частицы очень высока. Предельная температура жидкости в реакторе составляет 102С. В то же время температура плавления сульфенамида Т равна 105-109С. Таким образом, плавления частиц сульфенамида Т в реакторе не происходит. Можно лишь предполагать, что если это вещество является аморфным, то происходит некоторое размягчение поверхности частиц, которое и обуславливает их агломерацию в гранулы размером 2 мм.

В свете сказанного, проанализируем нестационарное температурное поле в отдельной частице сульфенамида Т. Считаем, что температура жидкости в реакторе однородна по объему и изменяется во времени по экспоненциальному закону (5). Частицы суспензии обладают тепловой инерцией, и их температура несколько отстает от температуры окружающей жидкости. Кроме того, температура поверхности частицы несколько выше температуры центральной ее части. Пусть частица имеет сферическую форму диаметром 70 мкм (ее радиус R=35*10^-6 м).

Имеем задачу определения температурного поля внутри шара, когда он омывается жидкостью, температура которой изменяется во времени t и определяется функцией t. Задача определения температуры внутри шара при произвольном изменении температуры омывающей среды в виде Fо сводится к решению уравнения теплопроводности:

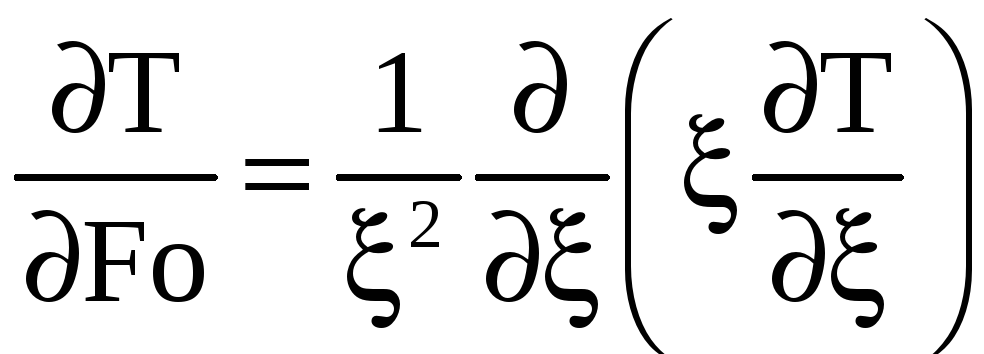, (6)

при условиях:

Fо = 0, T(  Fо) = T₀, ,  ,

где  = r/R  Fо = at/R².

Второе граничное условие получим из следующих соображений. Теплообмен между телом и внешней средой через поверхность соприкосновения S происходит по закону Ньютона:

q = - n_s = t_s ,

где  - коэффициент теплоотдачи; n – внешняя нормаль к изотермической поверхности. Это соотношение преобразуем в граничное условие

= 1, +Вi Вi(Fo), (8)

где Вi=R_ч  критерий Био, _ч коэффициент теплопроводности материала частицы.

В частом случае (см. формулу (5))

(Fo)=₀1-exp(-PdFo), (9)

где =Т_к-Т₀, Pd= KF(R²)/ (cV_a).

Формулу (5) можно привести к виду (9) следующим образом. Запишем (5) так: =_к- exp(-PdFo)( Т_к-Т₀). Прибавим и вычтем из правой части (Т_к-Т₀)

=_к- exp(-PdFo)( Т_к-Т₀)+ (Т_к-Т₀)- (Т_к-Т₀),

или

=₀1-exp(-Pd^.Fo).

Решение задач (6)(8),(9) дано в 7 и имеет вид

=1-exp(-PdFo)+(АPd/[6(А-Pd)]{exp(-AFo)–exp(PdFo)}( - ²),

где А= 21Bi(Bi+5)/(2Bi²+14Bi+35).

Чтобы найти изменение температуры центра частицы в (10), необходимо положить =0. Соответственно, температуре поверхности отвечает =1.

Для анализа формулы (10) необходимо знать теплофизические свойства сульфенамида Т: _ч=0,3 Втм²К  _ч=1270 кгм ³ С_ч=1000 Дж кг К. Откуда коэффициент температуропроводности частиц а=_ч/(_ч С_ч)=0.3(1270_*10³)= 2,36_*10^-7 м²с.

Находим критерии

Bi= _чR _ч= {20658 35 (10^-6) }0,3 =2,4; Pd=(KFR²) (CV_a) =

=(1456 13.85 35 (10²) ³)((10^-12) 4190 3.115 2.36 (10^-7))=0.8 (10^-5).

Здесь V_a=3.115 м³ - объем суспензии в реакторе, F DH+(D²)4_*1.8_*2+(_*1.8 )/4=13.85 м² ; _к  коэффициент теплоотдачи от стенок реактора; _ч  коэффициент теплоотдачи на поверхности частицы.

Согласно численному значению Bi внешнее и внутреннее термические сопротивления соизмеримы. Задача сопряженная.

Пользуясь соотношением (5), найдем время прогрева жидкости в аппарате от 30C до 100С. Можем записать

t= - V_aC/ KF ln[(T_k-T_p )/(T_k-T_o)],

где T_p=100С. Подставив численные значения, находим время: t= 250 c  410

ЛИТЕРАТУРА

1. Касаткин А. Г. Основные процессы и аппараты химической технологии. - М.: Химия, 1971.-784 с.

2. Павлов К.Ф., Романков П. Г., Носков А. А. Примеры и задачи по курсу процессов и аппаратов химической технологии.-Л.: Химия, 1987.-576с.

3. Романов П. Г., Курочкина М. И., Мозжерин Ю. Я. Процессы и аппараты химической промышленности. - Л.:Химия,1989.-560с.

4. Берд Р.,Стьюард В., Лайтфут Е. Явление переноса. - М.:Химия,1974.-688с.

5. Брагинский Л. Н., Бегачев В. И., Барабаш В. М. Перемешивание в жидких средах.-Л.:Химия,1984.-336с.

6. Лыков А.В. Тепломассообмен:(Справочник).-М.:Энергия,1978.-480с.

7. Цой П.В. Методы расчета задач тепломассопереноса. М.: Энергоатомиздат, 1984.-416с.

Приложение 4. Фрагмент выпускной бакалаврской работы Приваловой Ю.В. на тему «Теплообмен при переработке резиновых смесей в периодическом смесителе»

Цель процесса смешения – достижение определенного пространственного распределения частиц относительно друг друга и их диспергирование.

Нагревание или охлаждение, саморазогрев, теплоотвод и теплопередача имеют большое значение, как в технологических процессах производства технических изделий, так и при их эксплуатации. Тепло – один из наиболее важных факторов технологического процесса в производстве резины.

Интересно проанализировать изменение среднеобъемной температуры смеси в процессе перемешивания. Камеру резиносмесителя будем рассматривать как неизотермический реактор периодического действия. Разогрев смеси обусловлен диссипативным тепловыделением за счет поглощения механической энергии деформации. Выделяющееся тепло отводится посредством поверхности ротора и стенок камеры. Недостаточный теплоотвод может привести к вулканизации резины, что снижает ее качество. Для отвода тепла ротор и стенки камеры выполняются полыми (для подачи охлаждающей воды). Регулируя расход воды и ее температуру, можно управлять тепловым режимом смесительной камеры.

Баланс тепла в процессе смешения при его тепловом моделировании записывается уравнением[8]:

(3.32)

где c - теплоемкость перемешиваемой среды; ρ – плотность; V – объем смесительной камеры; T – температура; t – время; N=Nдвּη - подводимая мощность[2]; Nдв- мощность двигателя; - КПД передачи; K – коэффициент теплопередачи; F – поверхность смесительной камеры; Тв - средняя температура охлаждающей воды.

Используемые в практике смесители имеют комплексный коэффициент теплопередачи порядка 200 – 800 Вт/м²ּК.[8]

Для установившегося теплового состояния dT/dt=0 и среднюю температуру смеси можно определить T=T_B+N/(KF). Однако для достижения такого режима необходимо время, превышающее продолжительность смешения. Пусть в начальный момент времени t=0 температура смеси была T=T₀. Проинтегрировав уравнение теплового баланса с учетом указанного начального условия, получим выражение, описывающее кинетику изменения температуры смеси.

. (3.23)

Как было показано выше, подводимую мощность можно приближенно определить как произведение мощности двигателя на КПД передачи. В то же время существует более точная формула для расчета полезной мощности вязкого трения, которая для случая наклонной лопасти имеет вид[7]

, (3.24)

где: υ – окружная скорость гребня лопасти; ℓ – ширина края лопасти; В – длина ротора; h₀ - зазор между краем лопасти и стенкой цилиндра.

Выполним оценку мощности по этой формуле, взяв данные из технической характеристики рассматриваемого резиносмесителя: h0=3ּ10^-3 м; n=37 об/мин; ℓ=0,015 м; В=0,85 м.

Найдем эффективную вязкость резины.

Для степенного реологического уравнения касательное напряжение определяем по формуле [5,8]: , где ₀=926000 Пасⁿ; n=0,25.

Оценка для скорости сдвига в рабочем зазоре[7]:

γ≈υ/h_о=1,065/0,003=355 1/с.

Находим эффективную вязкость по формуле[5]. Подставив в формулу (3.24), получаем

Используя интегральное уравнение теплового баланса, найдем конечную температуру охлаждающей воды. Уравнение теплового баланса имеет вид[2]

.

Согласно техническим характеристикам: G=2.778 Кг/с; Т_н=278…298 К, принимаем, равное 293 К. При этом N=280000 Вт.

Из этой формулы получаем выражение для конечной температуры:

.

Подставив численные значения, найдем Т_к=353 К.

Пользуясь полученным выражением (3.23), можно подобрать режим охлаждения, соответствующий технологическим требованиям.

Представленная модель разогрева смеси построена для случая постоянной вязкости резины, т. е. не учитывает зависимость вязкости от температуры. В реальных условиях вязкость зависит температуры. Согласно выражению (3.24) тепловыделение в камере пропорционально вязкости смеси. Используем аррениусову зависимость вязкости от температуры.

,

где: μ_о – вязкость при температуре Т₀; Е – энергия активации, Дж/моль; R=8,31 Дж/(мольּК) – универсальная газовая постоянная.

При построении математической модели достаточно в расчетное выражение поставить рядом с мощностью в качестве сомножителя экспоненциальную функцию, т. е. уравнение теплового баланса записать так:

(3.25)

Интеграл этого уравнения не выражается через элементарные функции, поэтому воспользуемся методом механических квадратур (с помощью программы MathCAD).

Согласно данным [5] энергия активации для резиновой смеси составляет Е=50000 Дж/моль при Т_а=333 К. Кроме того, при расчете использовались следующие значения параметров: С=2000 Дж/(кгּК) [8]; ρ=1200 кг/м³ [8]; F=4 м²; К=700 Вт/(м²ּК); Т_о=293 К; V=ּ0,6 м³; Т_в=278 К; N=280000 Вт. Интервал времени t=0…500 с.

Рассмотрен случай постоянной вязкости. Расчеты выполнены по формуле (3.23). Построен график зависимости температуры от времени смешения, который представлен на рисунке 3.2.

Кроме того, получено численное решение дифференциального уравнения (3.25). Результаты решения представлены на графике рис. 3.3. Видно, что с учетом температурной зависимости вязкости характер кинетики существенным образом изменяется. Появляется экстремум температуры в начале процесса перемешивания при t≈5 с. При этом температура

Рис. 3.2. Зависимость температуры от времени в случае постоянной вязкости резиновой смеси.

Рис. 3.3. Изменение температуры в камере смешения (T) во времени (t) с учетом аррениусовой зависимости вязкости смеси от температуры.

превышает равновесное значение на 20ºК. Далее температура экспоненциально понижается до уровня, соответствующего установившемуся режиму. Причем ввиду пониженной вязкости на участке t≥50 с. равновесная температура ниже, чем в случае постоянной вязкости (см. рис.3.2). Результаты вполне соответствуют физическим представлениям о процессе. Всплеск температуры обусловлен высокой начальной вязкостью резиновой смеси, которую предсказывает закон Аррениуса. В начальный момент имеет место большая нагрузка на роторы и подшипники. Следовательно, при загрузке рабочей камеры смесителя необходимо контролировать температуру смеси или ее консистентность. Прочностной расчет деталей камеры и ротора следует выполнять по начальной вязкости резины, т.е. для пускового момента.

Литература

1. Белозеров Н.В., Технология резины. – М.: Химия, 1979. – 472 с.

2. Басов Н. И., Казанков Ю. В., Любартович В. А., Расчет и конструирование оборудования для производства и переработки полимерных материалов. – М.: Химия, 1986. – 488 с.

3. Бекин Н. Г., Шанин Н. П., Оборудование заводов резиновой промышленности. – Л.: Химия, 1978. – 400 с.

4. Барсков Д. М., Машины и аппараты резинового производства. – М.: Химия, 1975 – 600 с.

5. Торнер Р. В., Теоретические основы переработки полимеров. – М.: Химия, 1977.

6. Скачков А.С., Левин С.Ю. Оборудование заводов резиновой промышленности. – М.: Высшая школа, 1968 – 348 с.

7. Бернхардт Э., Переработка термопластичных материалов. – М.: Госхимиздат, 1962. – 747 с.

8. Вострокнутов Е. Г., Виноградов Г. В., Реологические основы переработки эластомеров. – М.: Химия, 1988. – 232 с.

Приложение 5. Фрагмент выпускной бакалаврской работы Мандрона Н.И. на тему «Аналитическое исследование тепловыделения в межвалковом зазоре при измельчении резины».

Как показал обзор литературных источников, в настоящее время отсутствуют теоретические модели измельчения резины на валках. Имеются лишь многочисленные экспериментальные данные о влиянии режимов на процесс измельчения. При ряде упрощающих допущений выполним инженерную оценку процесса, используя общеизвестные физические представления.

Во-первых, найдем распорное усилие. Считаем измельчаемый материал сплошной резиновой полоской начальной толщиной _0. Изменение механических свойств резины, связанное с разрушением, не учитываем. Таким образом, получим оценку действующих усилий и теплового эффекта с некоторым избытком “сверху” Радиусы валков R₁ и R₂. Расчетная схема представлена на рис. 1.

Рис. 1. Схема деформации резины в валковом зазоре.

При определении распорного усилия не имеет значения вращение валков. Выделим в зоне деформации участок длиной dx. Ширина валков B. Координата x₀ характеризует начало зоны деформации, x₁-ее конец. Причем x₀ определяется начальным размером куска резины, а x₁-конечным. Резина при больших деформациях проявляет эластические свойства, поэтому в этом случае закон Гука неприменим. Считаем, что в зазоре имеет место деформация чистого сдвига. Чистый сдвиг определяется как чистая однородная деформация, в которой одно из главных растяжений равно единице (по ширине валка) и объем неизменен. В работе [1] показано, что напряжение  в случае чистого сдвига определяется выражением

(1)

где G=E/3-модуль сдвига, E-модуль растяжения, =l/l₀ -относительная деформация, l₀-начальная длина образца, l-текущая.

Зависимость (1) показала хорошее соответствие с наблюдаемыми результатами в широком диапазоне деформаций.

При перемещении полосы от сечения x₀ до x она уменьшается в толщине от l₀ до l. Текущая толщина пластины связана с координатой x. Из геометрических соображений следует

(2)

(3)

Последнее выражение записано с учетом малости зоны течения x<<R.