1.10. Фильтрация через неподвижные пористые слои. Закон Дарси

Для мудрости нет ничего ненавистнее мудрствования.

Сенека

В технике широко распространены различного типа фильтры для жидкостей. Кроме того, неподвижный зернистый слой непосредственно используется в таких процессах как абсорбция, адсорбция (противогаз), движение смеси газов или жидкостей в слое зернистого катализатора и т.д.

При этом возникает задача определения гидравлического сопротивления слоя с целью обоснованного подбора насоса или компрессора.

Экспериментально установлено, что в мелкозернистом слое при малых скоростях среды имеет место линейная зависимость скорости жидкости от градиента давления. Этот закон был открыт Дарси в 1854 г. при исследовании движение воды в слое песка. Записывается закон следующим образом:

,

где _х- средняя скорость движения воды, К₁- коэффициент фильтрации.

Коэффициент фильтрации зависит от свойств зернистого слоя и вязкости жидкости. Для фильтрации воды в песке К₁=10^-2 –10^-4 м/с. В случае непроницаемого материала К₁=0. Чтобы исключить зависимость коэффициента фильтрации от вязкости, был введен коэффициент проницаемости слоя К, а закон Дарси предложено записывать в форме

.

Из сопоставления представленных двух форм уравнения Дарси следует соотношение между коэффициентами .

При этом коэффициент проницаемости К зависит только от геометрических свойств слоя (пористости, диаметра частиц), но не от вязкости жидкости. В качестве примера аналитического расчета коэффициента проницаемости, можно привести формулу Козени для слоя сферических частиц

,

где d- диаметр зерен,  - пористость.

Закон Дарси правомерен только для ламинарного режима течения. Поэтому верхняя граница применимости закона определяется числом Рейнольдса .

1.10.1. Фильтрация через плоскую пористую стенку

…наука является областью наибольшего бескорыстия.

М. Горький

Задачей расчета фильтрации является определение зависимости расхода жидкости от перепада давления. Для решения задач фильтрации последовательно используются уравнение неразрывности и закон Дарси. Схема фильтрационного движения жидкости через плоскую стенку представлена на рис. 1.23. Фильтрационный поток одномерен, поэтому для

компонент скорости имеем _y=_z=0. Следовательно, уравнение неразрывности в прямоугольных координатах имеет вид

.

Из этого уравнения можно сделать вывод, что осевая компонента скорости постоянна

С другой стороны, согласно закону Дарси,

.

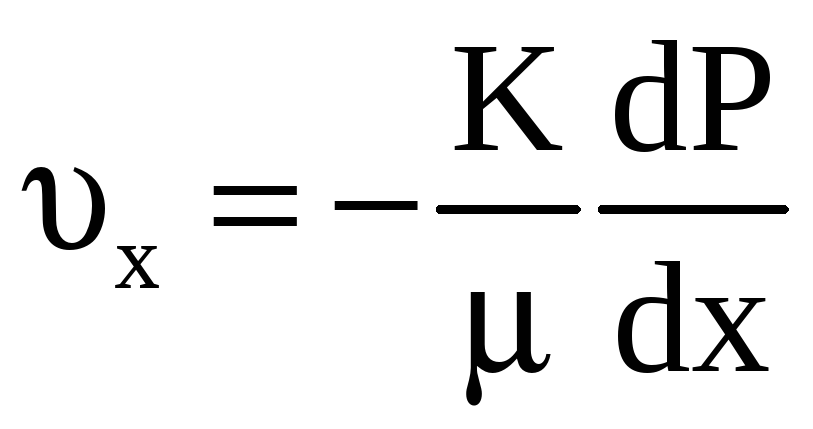Граничные условия задачи состоят в задании давлений на поверхностях пористой пластины

х=0, Р =Р₁,

х=, Р =Р₀ , (Р₁>P₀).

В уравнении Дарси разделим переменные и проинтегрируем, учитывая, что _х= const

.

Имеем линейную зависимость давления от координаты

.

Скорость _х неизвестна. Найдем ее, используя граничное условие х =, Р=Р₀,

.

Откуда

.

Расход равен произведению скорости на площадь сечения стенки

,

где Н- высота стенки, В – ширина стенки. Подставив выражение для скорости, имеем

.

Распределение давления в стенке найдем следующим образом. Для скорости имеем

.

С другой стороны

.

Из совместного рассмотрения этих зависимостей получаем линейное распределение давления по толщине стенки

.

Отметим, что полученное выражение для расхода жидкости может быть использовано для экспериментального определения коэффициента проницаемости

.

Пример.

Найти коэффициент проницаемости плоской пористой стенки толщиной 3 мм при фильтрации воды (вязкость 10^-3 Па^.с). Площадь поверхности 5 см², расход жидкости 0,5 мл/с, перепад давления 10⁵ Па.

Решение.

Воспользуемся формулой

.

Откуда для коэффициента проницаемости можем записать

.

Учитывая формулу для скорости фильтрации

,

запишем

.

Подставим численные значения параметров

.

Задачи.

1. Найти расход жидкости, протекающей через пористую пластину площадью 10 см², если ее коэффициент проницаемости К=10^-10 м², вязкость жидкости 10^-3 Па^.с, толщина пластины 5 мм и перепад давления 10 ат.

2. Во сколько раз возрастет расход жидкости, если давление фильтрации увеличить в 2 раза?