§33. Теорема Чебышева.

Случайные величины сходятся по вероятности к величине A (случайной или неслучайной), если для любого вероятность события при стремится к единице, то есть (или). Сходимость по вероятности символически записывают так: .

Сходимость по вероятности требует, чтобы неравенство выполнялось для подавляющего числа членов последовательности (в математическом анализе – для всех , где N – некоторое число), а при практически все члены последовательности должны попасть в -окрестность A.

Теорема 6 (Теорема П. Л. Чебышева). Если случайные величины независимы и существуют такое число , что , то для любого

то есть среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

.

Неравенство Чебышева для средней арифметической случайных величин, то есть для можно записать в виде:

Следствие. Если случайные величины независимы и одинаково распределены, , , то для любого

то есть среднее арифметическое случайных величин сходится по вероятности к математическому ожиданию a:

.

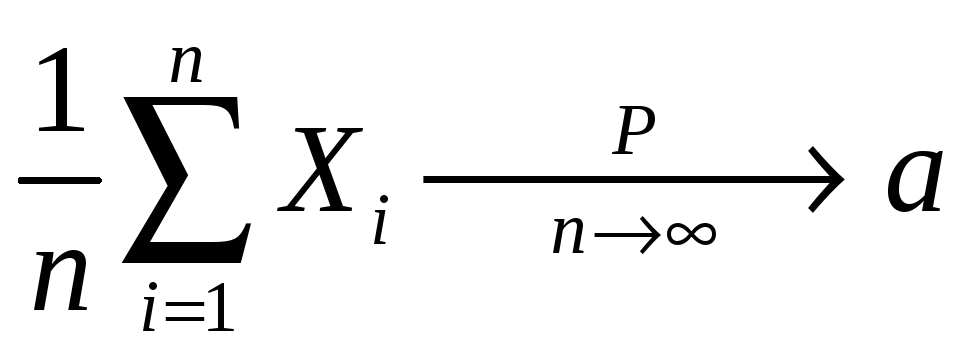В этом случае неравенство (5.6) примет вид:

Следствие теоремы Чебышева обосновывает «принцип среднего арифметического случайных величин », постоянно используемый на практике. Так, пусть произведено n независимых измерений некоторой величины, истинное значение которой а (оно неизвестно). Результат каждого измерения есть случайная величина . Согласно следствию (5.6), в качестве приближенного значения величины a можно взять среднее арифметическое результатов измерений:

Равенство тем точнее, чем больше п.

На теореме Чебышева основан также широко применяемый в статистике выборочный метод, суть которого в том, что о качестве большого количества однородного материала можно судить по небольшой его пробе.

Теорема Чебышева подтверждает связь между случайностью и необходимостью: среднее значение случайной величины практически не отличается от неслучайной величины .

Пример 65. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения ламп во всей партии менее чем на 5 ч (по абсолютной величине), если известно, что среднее квадратическое отклонение продолжительности горения ламп в каждом ящике меньше 7 ч.

Решение: Пусть - продолжительность горения электролампы, взятой из ящика (ч). По условию дисперсия . Очевидно, что средняя продолжительность горения отобранных ламп равна , а средняя продолжительность горения ламп во всей партии . Тогда вероятность искомого события по формуле (5.6): , то есть не менее, чем 0,9902.

§34. Теорема Бернулли.

Теорема 7 (Теорема Я. Бернулли). Если вероятность появления события A в одном испытании p, число наступления этого события при n независимых

испытаниях равно , то для любого числа имеет место равенство

то есть относительная частота события A сходится по вероятности к вероятности p события A: .

Теорема Бернулли теоретически обосновывает возможность при­ближенного вычисления вероятности события с помощью его относи­тельной частоты. Так, например, за вероятность рождения девочки можно взять относительную частоту этого события, которая, соглас­но статистическим данным, приближенно равна 0,485.

Неравенство Чебышева для случайных величин принимает вид

Обобщением теоремы Бернулли на случай, когда вероятности появления события А в каждом из n испытаний различны, является теорема Пуассона:

где — вероятность события A в испытании.

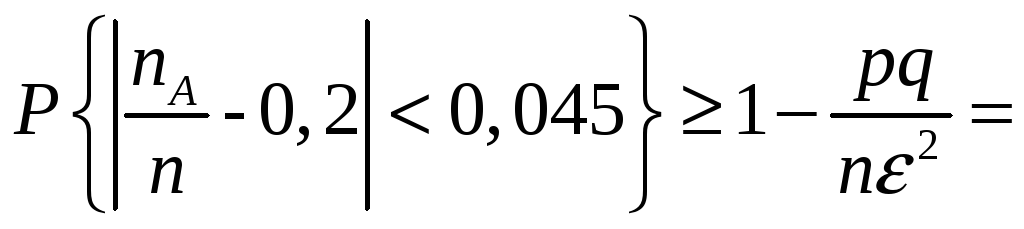
Пример 66. Вероятность наличия опечатки на одной странице руко­писи равна 0,2. Оценить вероятность того, что в рукописи, содержащей 400 страниц, частость появления опечатки отличается от соответству­ющей вероятности по модулю меньше, чем 0,04. Воспользуемся формулой (5.10). В данном случае . Имеем , то есть .