Глава 5. Предельные теоремы теории вероятностей.

§31. Закон больших чисел.

Закономерности, изучаемые в курсе теории вероятностей, получены из реальных статистических закономерностей, свойственных массовым случайным явлениям. Они связаны с массовостью явлений: с большим числом выполняемых однородных опытов или с большим числом наблюдений, опытов или воздействий, которые характеризуются случайной величиной, подчиненной определенному закону. Изучение закономерностей, проявляющихся в массовых случайных явлениях, позволяет научно предсказать результаты будущих испытаний.

Свойство устойчивости массовых случайных явлений означает, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате таких явлений в общей совокупности; случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в массе нивелируются, погашаются, выравниваются. Наблюдается устойчивость средних величин, к которым и стремится значение случайной величины при большом количестве наблюдений.

В узком смысле слова под «законом больших чисел» в теории вероятностей понимаются несколько математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Простейшая из них — теорема Бернулли. Она утверждает, что при большом числе опытов частота события приближается к вероятности этого события.

Закон больших чисел играет важную роль в практических применениях теории вероятностей. Свойство случайных величин при определенных условиях вести себя практически как неслучайные позволяет уверенно оперировать этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.

Возможности таких предсказаний в области массовых случайных явлений еще больше расширяются наличием другой группы предельных теорем, касающихся уже не предельных значений случайных величин, а предельных законов распределения. Это центральная предельная теорема. Различные формы центральной предельной теоремы различаются между собой теми условиями, для которых устанавливается это предельное свойство суммы случайных величин.

Различные формы закона больших чисел вместе с различными формами центральной предельной теоремы образуют совокупность так называемых предельных теорем теории вероятностей. Предельные теоремы дают возможность не только осуществлять научные прогнозы в области случайных явлений, но и оценивать точность этих прогнозов.

§32. Неравенства Маркова и Чебышева.

Неравенство А. А. Маркова. Если X – неотрицательная случайная величина, имеющая математическое ожидание , то для любого имеет место неравенство

Оно дает оценку вероятности попадания случайной величины в промежутке .

Неравенство (5.1) можно записать в форме

Пример 62. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) будет не менее 400; б) не превысит 500.

Решение: а) По условию . По формуле (5.1) , то есть вероятность того, что число вызовов будет не менее 400, будет не более 0,75; б) По

формуле (5.2) , то есть вероятность того, что число вызовов не превысит 500, будет не менее 0,4.

Неравенство П. Л. Чебышева. Если случайная величина X имеет математическое ожидание и дисперсию , то для любого справедливо неравенство Чебышева

Неравенство (5.3) дает оценку вероятности попадания случайной величины X в область, лежащую вне промежутка .

Неравенство Чебышева можно записать в форме

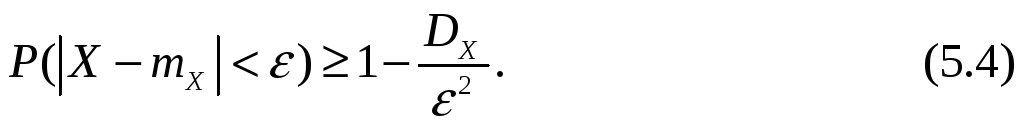
Пример 63. Оценить с помощью неравенства Чебышева вероятность того, что отклонение случайной величины X от своего математического ожидания будет меньше трех средних квадратичных отклонений, то есть меньше .

Решение: Полагая в формуле (5.4), получаем .

Эта оценка называется «правилом трех сигм»; для случайной величины эта вероятность равна 0,9973.

Пример 64. Средний расход воды на животноводческой ферме составляет 1000 л в день, а среднее квадратичное отклонение этой случайной величины не превышает 200 л. Оценить вероятность того, что расход воды на ферме в любой выбранный день будет меньше 2000 л, используя: а) неравенство Маркова; б) неравенство Чебышева.

Решение: а) Пусть X – расход воды на животноводческой ферме (л). По условию . Используя неравенство Маркова (5.2), получим , то есть не менее 0,5; б) Дисперсия . Так как границы интервала симметричны относительно математического ожидания , то для оценки вероятности искомого события можно применить неравенство Чебышева (5.4): 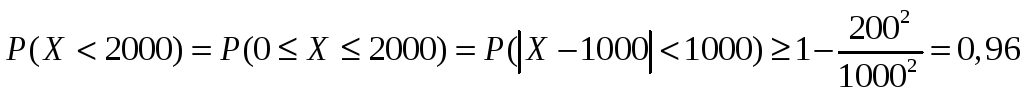, то есть не менее чем 0,96. В данной задаче оценку вероятности события, найденную с помощью неравенства Маркова , удалось уточнить с помощью неравенства Чебышева .