31. Кодирование чисел

Количественно информацию обычно представляют в двоичном виде (в виде двоичных чисел), т.к. два противоположных состоя­ния легко воспроизводятся многими техническими средствами и распоз­наются с весьма высокой вероятностью. При этом соответствующие сигналы обозначают, т.е. их кодируют зна­чениями 0 и 1. Подобным же обра­зом, используя двоичное решающее правило, кодируют и многоразрядные числа. Основание таких чисел равно 2 (у десятичных равно 10). Показатели степеней двоичного числа сум­мируют по модулю 2. Так, напри­мер, десятичное число 235 в двоич­ном виде записывают следующим образом: 12⁷ + 12⁶ + 12⁵ + 02⁴ +12³ + 02²+12¹ + 12⁰= 128 + 64 + 32 + 8 + 2 + 1 = 235. Каждый разряд двоичного числа обозначен 0 или 1, а двоичные числа представляются общим выражением

,

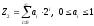где а_i - целое число (0 или 1).

Количество информации Н= lb m = lb (1 / r_v) бит.

Известно множество кодов, каж­дый из них имеет свои достоинства и недостатки. Поэтому в измери­тельной технике, в зависимости от вида и назначения сигнала (обработ­ка, отображение данных или их пе­редача), применяют соответствую­щие виды кодирования. Чаще всего для этого используют двоичный код. Разряды слов в этом коде пред­ставлены двоичными значениями. В табл. 4.1 приведены десятичные числа от 0 до 9 и соответствующие им числа в так называемом двоич­но-десятичном коде (точнее, одной из разновидностей такого кода, с «весами» разрядов 4-разрядного ко­дового слова, равными 1-2-2-4 и со­ставляющими в сумме одноразрядное десятичное число - тетраду, ко­дированное двоично). Любое деся­тичное число записывают в виде на­бора таких тетрад (разрядов).

Весовые коэффициенты разрядов (тетрад) двоично-десятичного кода могут иметь и другие значения.

Таблица 4.1

Десятичное число	Коды разрядов тетрады				Тетрада
	4	2	2	1
0	0	0	0	0	0000
1	0	0	0	1	0001
2	0	0	1	0	0010
3	0	0	1	1	0011
4	0	1	1	0	0110
5	0	1	1	1	0111
6	1	0	1	0	1010
7	1	0	1	1	1011
8	1	1	1	0	1110
9	1	1	1	1	1111

Ча­ще других используют значения 8-4-2-1, которые в сумме (в каждой тетраде) также не превышают 9. На­пример, трехразрядные десятичные числа в таком коде представляют следующим образом:

752: 0111 0101 0010

или

913: 1001 0001 0011.

Такой двоично-десятичный код яв­ляется избыточным (т.к. в нем не используются возможности записи чисел от 10 до 15), однако это свой­ство позволяет распознавать ошиб­ки в результатах измерений, если они представляются указанными чис­лами в отдельных тетрадах (соот­ветствующие кодовые комбинации являются запрещенными).

В рассмотренных кодах при воз­растании чисел на 1 в некоторых комбинациях происходит «перенос» единиц из младших разрядов в бо­лее старшие. В ряде случаев измере­ний (например, при шуме), когда эта 1 не определена четко, могут появ­ляться ошибочные числа, в которых ошибка превышает 1. Для таких случаев используют код Грея, обес­печивающий увеличение числа (в том числе в случае неопределен­ности) только на 1, если оно воз­растает на 1, в ближайшем соседнем старшем разряде каждой тетрады. Представление десятичных чисел от 0 до 15 кодом Грея показано в табл. 4.2.

Правило записи, напри­мер десятичного числа 13, в коде Грея таково:

.

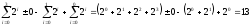При этом «веса» разрядов тетрады составляют (± 15), (± 7), ( 3), (± 1).

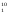В измерительной технике исполь­зуют также избыточные коды вида (), исправляющие ошибки, в част­ности (), т.е. 10-разрядный код с «весами» разрядов от 0 до 9 (код 1 из 10).

Таблица 4.2

Десятичное число	Разряды тетрады кода Грея					Тетрады		Пересчет обычного двоичного кода в код Грея
	( 15)	( 7)	( 3)	( 1)
0	0	0	0	0	0000		0000
1	0	0	0	1	0001		0001
2	0	0	1	1	0011		00+(1+2-1)
3	0	0	1	0	0010		00+(1+2) 0
4	0	1	1	0	0110		0+(1+2+4)-(1+2)+(1)
5	0	1	1	1	0111		0+(1+2+4)-(1+2)+(1)
6	0	1	0	1	0101		0+(1+2+4)0-(1)
7	0	1	0	0	0100		0+(1+2+4)00
8	1	1	0	0	1100		+(1+2+4+8)-(1+2+4)00
9	1	1	0	1	1101		+(1+2+4+8)-(1+2+4)0+(1)
10	1	1	1	1	1111		+(1+2+4+8)-(1+2+4)+(1+2)-(1)
11	1	1	1	0	1110		+(1+2+4+8)-(1+2+4)+(1+2)0
12	1	0	1	0	1010		+(1+2+4+8)0-(1+2)0
13	1	0	1	1	1011		+(1+2+4+8)0-(1+2)+(1)
14	1	0	0	1	1001		+(1+2+4+8)00-(1)
15	1	0	0	0	1000		+(1+2+4+8)000