Задача 1.7

Под каким давлением (рисунок 1.7) нужно подать жидкость в безштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо, преодолевая силу на штоке, если давление в штоковой полости ? На какую силу сжатия нужно отрегулировать пружину предохранительного клапана, чтобы он открывался при возрастании силы на штоке до величины , если диаметр входного отверстия (седла) клапана , а давление . Силы трения не учитывать.

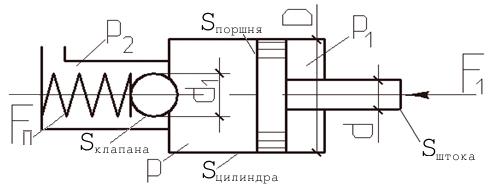
Рисунок 1.7

Таблица исходных данных:

Диаметр, мм	Давление, МПа	Сила, Н

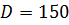
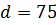
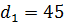
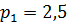
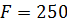
Решение:

1. Для движения штока необходимо, чтобы сила давления в бесштоковой полости равна 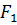+сила давления от 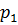. Таким образом:

где

Следовательно,

Отсюда выражаем давление, под которым нужно падать жидкость в бесштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо:

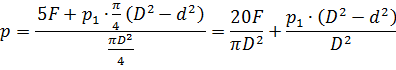
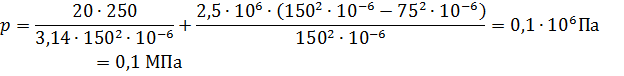
2. При силе на штоке в

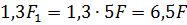
в бесштоковой полости:

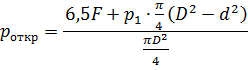
Для открытия клапана необходимо равенство сил слева и справа от него:

Определяем силу сжатия , на которую нужно отрегулировать пружину предохранительного клапана, чтобы он отрывался при возрастании силы на штоке до величины :

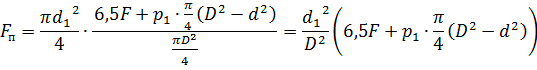
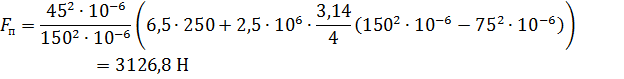
Ответ:

Задача 1.9

Определить осадку и проверить остойчивость плавания в воде деревянного бруса (рисунок 1.9). Размеры бруса: высота , ширина , длина . Относительная плотность бруса . Вычислить наименьшую высоту , при которой брус будет еще остойчив.

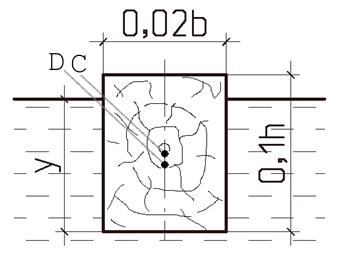
Рисунок 1.9

Таблица исходных данных:

Относительная плотность	Плотность воды, кг/м3	Длина, м	Ширина, м	Высота, м

Решение:

Для определения осадки бруса записываем условие плавания:

Относительная плотность бруса:

Поскольку брус – однородное прямоугольное тело, его центр тяжести (т.С) находится на середине высоты . Центр водоизмещения (т. D) лежит в центре тяжести объема погруженной части , т.е. на высоте от нижней кромки бруса. Т.к. т.С выше т.D на величину:

Для проверки остойчивости тела необходимо вычислить величину метацентричного радиуса .

Находим центральный момент инерции плоскости ватерлинии относительно продольной оси:

Тогда по формуле:

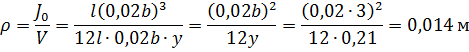
Т.к. , то брус не устойчив.

Ответ:

Задача 1.11

В вертикальной стенке, разделяющей резервуар на две части, расположено круглое отверстие с диаметром и насадкам длиной (рисунок 1.11). В наружной стенке имеется другое отверстие диаметром . Центры обоих отверстий расположены на высоте от дна. Уровень воды в левой части резервуара , расход через отверстия . Определить уровень воды в правой части резервуара и диаметр отверстия в наружной стенке.

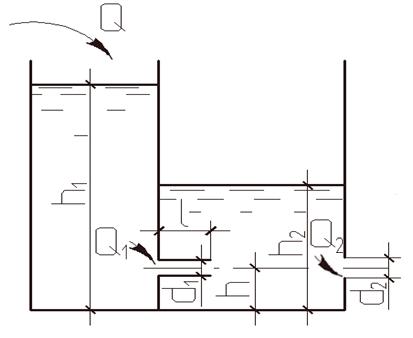
Рисунок 1.11

Таблица исходных данных:

Параметр	Расход, л/с	Вид насадка
		конический сходящийся

Решение:

Осредненные значения коэффициентов для режима истечения жидкости через конический сходящийся насадок для маловязких жидкостей (в нашем случае вода) следующие:

Коэффициент сжатия находим из соотношения:

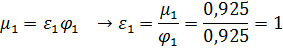
Запишем уравнение расхода :

Из этого уравнения находим скорость истечения в сжатом сечении струи:

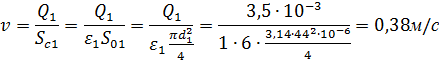
Определяем расчетный напор:

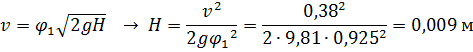
Так как , то и . Тогда:

Отсюда находим уровень воды в правой части резервуара:

Запишем уравнение расхода :

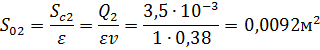
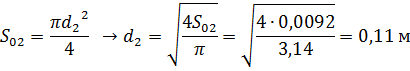
Ответ: