Особенность некогерентного приема пс-символов
-
Неког.обработка инверсных сигналов не производится
-
Некогер.обработка для ортогон. Сигналов
СФ1 ДО1
X
(t) ―
УПр
УПЧ
СФ2 ДО2 h=
ФС
X1
1
ДО
ФНЧ
__ +
X2 
2
ДО
ФНЧ
ГОПС ЭУ
UОП1 (t)= U1(t+Δ)+ U2(t+Δ)
UОП2 (t)= U1(t-Δ)+ U2(t-Δ)
Рош=0,5
ехр(
)
Быстрый поиск
Отвлечемся на реализацию быстрого поиска по временному положению
Быстрый поиск можно реализовать на генераторе М-посл. х3+х+1
(
1,0) ТИ
ПСП
1
2 3
Uвх(t)
2 1 ключ +
устройство
запоминания БУ
п
оложение
ключа: 1 – генератор
2 – поиск Ти С
БУ – блок управления
С – синтезатор опорных частот
В режиме поиска в регистр сдвига записываются первые элементарные символы приходящей ПСП и ключ переводят в положение 1.
Если записанные символы неискаженны, то опорный генератор начинает работать синхронно с приходящей последовательностью. Чтобы исключить влияние ошибки – накапливают и усредняют.
Автокорреляционный прием ПС – сигналов с ДФМи и информационной модуляцией по задержке (беспоисковый приемник)
х(t)= Si(t)+n(t)
0≤t≤T
Fn=
S
С(t) S1(t)
«1» - ПСП1
S2(t)
«0» - ПСП2
U2(t)= U1(t-t3) (циклическая временная задержка)
t3=(2n-1)
n=0,1,2…
Ui(t)=
А0
rect
[t-(j-i)τ0]
аij , j= I, N
τ0 – длительность символа ПСП
спектральная плотность ПСП:
F(ω)
0
ω
fT – тактовая частота ПСП
fT
=
,
в спектре отсутствует составляющая на
тактовой частоте
U(t)· U(t-τ)=z (t, τ); 0≤ τ≤ τ0
Спектральная плотность произведения Z(t,τ) :
Fz(t,τ)=A40
+
Мощность спектральной сост.на тактовой частоте (f= fT)
Рz(
,τ)=
Максимум мощности
получ.при τ=
Рz
(
,
)=
F(ω)
0
ω
F
z (f,
)
f
1/ τ0= fT
Можно показать, что при наличии сигналов с информационной модуляцией по задержке τ0 выделенное гармоничное колебание на fт будет манипулирована на (0;π) радиан по закону цифровой информации.
Покажем это:
П
усть
U1(t) UТ1=
=cos
ωTt
U
2(t)
UТ2=
=cos
[ωT(
t-(2n-1)
)]=
cos
[ωTt-
-ωT
(2n-1)
]=
cos
ωTt
,
ωT(2n-1)
=2π
fT(2n-1)
=2π
(2n-1)
=
π
(2n-1)
Из изложенного вытекает структура приемника
ЛЧ УПЧ СД Х ПФ СД2 ВУ УПР
t=τ0/2
Помехоустойчивость:
На вых.перемножителя
Zс(t,
)=
U(t)·
U(t-
)
Uсш(t)= U(t)+n (t)
Z
сш(t)=[
U(t)+n
(t)]
[ U(t-
)]+
n(t-
)=
U(t)
U(t-
)+
Zс(t)
+
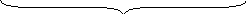U(t)+n
(t-
)+
U(t-
)
n
(t)+
n
(t)·
n(t-
)
F
z
(f,
)
Zсш(t)
Рzc=
;
Рzш
- ?
Корреляционная функция шумовой компоненты:
rzш(t1, t2)=< Zш(t1)· Zш(t2)>
Спектральная функция шумовой компоненты:
FZш(ω)=
γzш(τ)ejwtdt
В результате вычислений спектральная плотность на тактовой частоте примет вид:
FZш(fг)=2(A20N0+
)
Мощность шумовой составляющей на тактовой частоте в полосе информационного сигнала:
Рzш=
(1)= FZш(
)·ΔFu=2(A20N0+
)·ΔFu
Отсюда С/Ш на выходе ПФ:
g=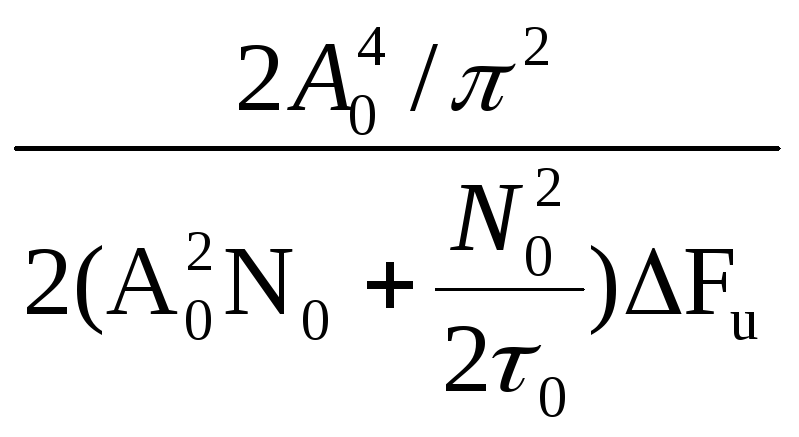
=
gвх=
g
=
·
Рош=1-Ф(
)=1-
Ф
- потенциальная помехоустойчивость автокорреляционного премника
Для сравния вспомним Рош для когер.приема с поиском
Рош
ког=1-Ф(
)
Сравним:
-
при
>>1
Рош
АК=1-
Ф(
)=1-Ф(
)
-
при
<<1
Рош
АК=1- Ф(
)
Автокорреляционный приемник проигрывает в помехоустойчивости когерентному ( для Рош=0,01 -> 4дБ ), но но не требует поиска по временному положению.