
- •Космические
- •1.Обобщенная структурная схема одноканальной рспи
- •Корреляционная функция
- •3.Основы теории информации. Количество информации, заключенной в одном дискрете (символе)
- •3.1 Информационные характеристики дискретных сообщенй
- •3.2 Скорость передачи информации, пропускная способность дискретного канала связи
- •3.4 Скорость передачи информации, пропускная способность канала связи при передачи непрерывных сообщений
- •4. Оптимальные приемники в системах передачи цифровой информации
- •Сверточные коды в рспи
- •Декодирование ск
- •2.Б) Бессиндромное декодирование ск:
- •Применение пс-сигналов в системах передачи цифровой информации
- •Когерентный прием пс-сигналов с дфМн и ортогонал.Информац.Модуляцией
- •Особенность некогерентного приема пс-символов
- •Быстрый поиск
- •Оценка времени поиска псп (последовательный метод поиска)
- •Применение ансамбля пс сигналов для передачи цифровой информации
3.4 Скорость передачи информации, пропускная способность канала связи при передачи непрерывных сообщений


 х
(t) КС у(t)
х
(t) КС у(t)
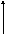
h (t)
П усть
х (t) (сообщение)
сигнал несущий сообщение носит случайный
характер подчин. Нормальному закону
распределения σ2x
усть
х (t) (сообщение)
сигнал несущий сообщение носит случайный
характер подчин. Нормальному закону
распределения σ2x
n(t) – белый шум - σ2n=N2·∆F
y(t) = x(t)+ n(t)
σ2y= σ2x+ σ2n
I(x,у)=
log2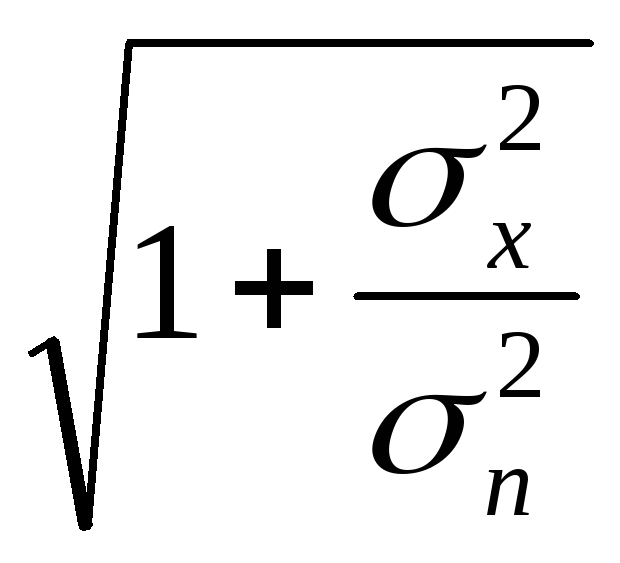 (бит) – среднее количество информации
(бит) – среднее количество информации
Ск=![]() (h
(у)- h
(у/х))
(h
(у)- h
(у/х))
Т – время анализа
С к Fк
– полоса частот отведенная для КС
к Fк
– полоса частот отведенная для КС
Т
=![]()
Ск=![]() log2
log2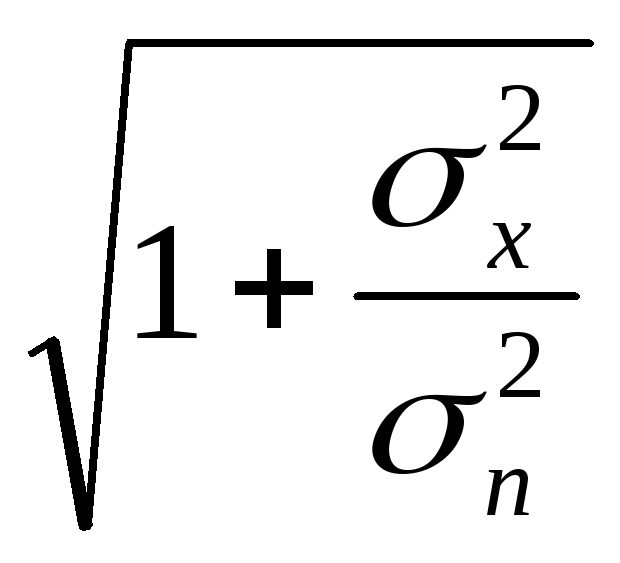 =
Fк
log2
=
Fк
log2
σ 2n= N0· Fк
σ 2n – дисперсия шума в полосе канала
Ск=
Fк
log2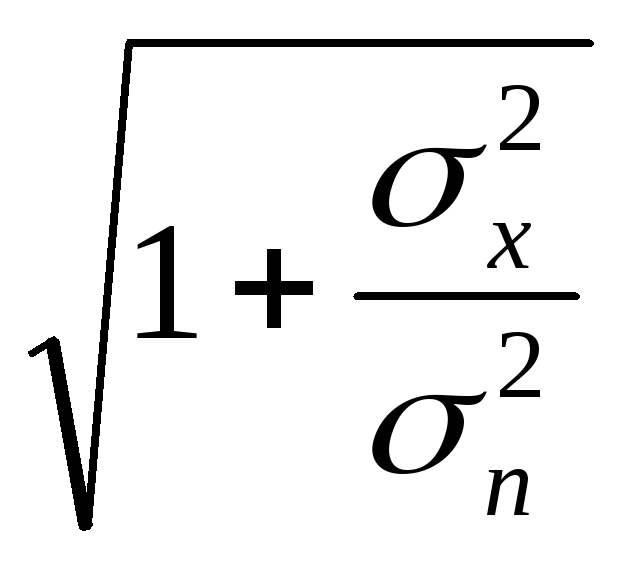 (бит/с)
(бит/с)
Ск=Rмакс
Н еобходимым
условием для не искаженной передачи
информации каналом связи Ск≥R
еобходимым
условием для не искаженной передачи
информации каналом связи Ск≥R
Ск 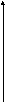









 0 Fк
0 Fк
![]() =gn
– отношение с/ш в полосе сигнала
=gn
– отношение с/ш в полосе сигнала
![]() =
gк
– отношение
с/ш в полосе канала
=
gк
– отношение
с/ш в полосе канала
N0 – односторонная спектральная плотность шума
Когда gк![]() 1,
Ск≈Fк
1,
Ск≈Fк![]() log2
log2
Ск=1,44
![]() (бит/с)
(бит/с)
R=Fэф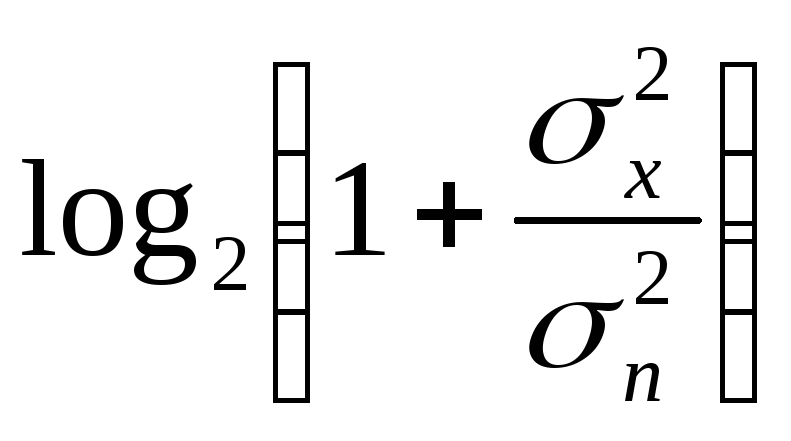 (бит/с)
(бит/с)
σ2nc= N0Fэф
Когда спектр.плотность шума меняется, то
Ск=![]() log2
log2![]() (бит/с)
(бит/с)
4. Оптимальные приемники в системах передачи цифровой информации
Методы приема: оптимальные и квазиоптические
4.1 Оптимальная обработка: когерентная и некогерентная
Квазиоптимальная: когер. и некогер.
Оптимальные различители сигналов
Х(t)=Si(t)+n (t), 0≤t≤T (T1=T2=T)
S
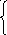 i(t)=
Si(t)
«1»
i(t)=
Si(t)
«1»
 Si(t)
«1»
Si(t)
«1»
Fn(ω)=![]() (на фоне белого шума)
(на фоне белого шума)
При передаче по символам, где символы – объединение нескольких бит
Количество бит в символе – к
а) к=2
« 00»-а1 S1(t)
00»-а1 S1(t)
« 10»-а2 S2(t)
10»-а2 S2(t)
« 01»-а3 S3(t)
01»-а3 S3(t)
« 11»-а4 S4(t)
11»-а4 S4(t)
Количество сигналов – m
m=4
б) к=3 к=2к=8
m >2
>2
 Si(t)
, i=1,m
Si(t)
, i=1,m
4.1.1. Оптимальный когерентный прием цифровых сигналов
m =2
=2





![]()



 - y
- y![]() y
y![]()
![]()
Х






 (t) (СД) УПР y
(t) (СД) УПР y![]()
![]()
![]()






 ЛФ УПЧ КД h
ЛФ УПЧ КД h
 СФ2
СФ2
Si(t) = S0i(t)coswit




СУ
gi(t)=C·Soi(T-t)
Soi(t) – огибающая сигнала
S(t)



 So(t)
So(t)
So(T-t)
С - коэффициент пропорциональности

T t (ослабление)
![]() =
=![]() ·
е-jφ(ω)
·
е-jφ(ω)
![]() =
=![]() ·
еjφ(ω)
·
еjφ(ω)
Рош=Р1·ф![]() +
Р2·ф(1-ф
+
Р2·ф(1-ф![]()
Р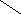 1=Р
(Si)
1=Р
(Si)
Р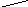 2=Р
(S2) вероятности
появления сигналов
2=Р
(S2) вероятности
появления сигналов
h - порог
h
=![]()
Е1=![]()
![]()
Е2=![]() R1,2=
R1,2=
![]() ·
·![]()
m1=<y1>=Е1-R1,2 - мат.ожидание
m2=<y2>=-Е2+R1,2
Если Е1 =Е2=Е (энергия огибающей)
Р1=Р2
Рош=1-ф![]()
ρ1,2
=![]() - коэффициент взаимной корреляции
- коэффициент взаимной корреляции
ф(х)![]()
![]() dt
- интеграл
вероятности
dt
- интеграл
вероятности
ф(0)=0,5
ф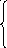 (∞)=1,
ф(-х)=1 - ф(х)
(∞)=1,
ф(-х)=1 - ф(х)
![]() = g
– простой сигнал
= g
– простой сигнал
g.В – сложный сигнал
В – база, В= Fэф·Т
σ2=![]() - дисперсия шума
- дисперсия шума
а) Амплитудная манипуляция с пассивной паузой
« 1» S1(t)
1» S1(t)
« 0» S2(t)=0
0» S2(t)=0
x




 (t)
(t)
Л




 Ф УПЧ КД СФ
УПР
Ф УПЧ КД СФ
УПР
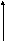



 Z h=E/2
Z h=E/2
 СУ
СУ

Рош=1-ф![]()
б) ЧМ – частотно-манипулированный сигнал
« 1» S1(t)=
S0(t)
cos ω1t
1» S1(t)=
S0(t)
cos ω1t
«
 0» S2(t)=
S0(t)
cos ω2t
0» S2(t)=
S0(t)
cos ω2t















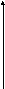










 УПР
УПР
 КД1
СФ1
КД1
СФ1
X(t)
-
ЛФ УПН КД2 СФ2 h=0
СУ
g(t)-С· S0(Т-t)
Если
![]() ≥
≥![]() ,
то ρ1,2=0
(т.е. сигналы ортогональны)
,
то ρ1,2=0
(т.е. сигналы ортогональны)
Рош=1-ф![]()
в) ФМН
ОФМн как метод борьбы с явлениями обратной работы
1 1 0
фаза
1 0
фаза
0 0 0
фаза
0 0
фаза
1 0 π
0 π
0 1 π
1 π

 КП bi
длительность цифрового бита
КП bi
длительность цифрового бита
а

 i bi
i bi

 +
+
д
 ля
(1;1)=>
ля
(1;1)=>
(0;1)


t3=T
аi= аi

 bi
bi 
 аi
аi




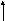
 ОКП
Фм
ОКП
Фм
Гн
b
 i аi
i аi

 +
+

 t3=T
t3=T
|
аi |
1 0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
с вых КП bi |
0 0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
с вых со bi |
0 0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
с вых ОКП аi |
1 0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |

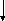

ОФМн



 Гн
Гн
С
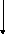
λ(t)


 S(t)
S(t)


 ИЦИ КП Фм
ИЦИ КП Фм
Когерентный прием простых цифровых сигналов с ОФМн
х(t)= Si(t)+n(t)
0 ≤t≤T
Fn=
≤t≤T
Fn=![]()
S 1(t)= S1(t)=
S0
cos (ω1t)
«1»
1(t)= S1(t)=
S0
cos (ω1t)
«1»
 S2(t)=
-S0(t)
cos (ω2t) «0»
S2(t)=
-S0(t)
cos (ω2t) «0»
х(t) 




 b1
i
b1
i
Л





 Ф УПЧ КД ВУ
УПР ОКП
Ф УПЧ КД ВУ
УПР ОКП
 а1i
а1i
 τ h=0
τ h=0
 СУ
СУ

а1i = b1i + b1 i -1
|
ИЦИ аi |
1 0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
с вых КП bi |
0 0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
с вых УПр b1i |
0 0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
с вых ОКП а1i |
1 0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
При сравнении аi и а1i 5 и 6 символы искажены т.е. ошибка удваивается при выходе с ОКП
1) b1i –символ искажен
b1 i -1 – правильный
2) bi –символ искажен
b i -1 – правильный
Р1 - вероятность ошибки
(1-Р1) – вероятность правильного приема
Р1(1-Р1)
Рош=2 Р1(1-Р1)
Р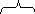 1=1-Ф(
1=1-Ф(![]() )
≈0,999÷0,999999
)
≈0,999÷0,999999
Рош=2[1-Ф(![]() ))1
Ф(
))1
Ф(![]() )≈2[1-Ф(
)≈2[1-Ф(![]() ))=
))=![]() exp[-g]
exp[-g]
Рош=(10-6-10-3)
Вывод: относительная фазовая манипуляция (ОФМн) позволяет избавиться от явления обратной работы, однако потенциальная ошибка при выявлении цифровых символов возрастает в 2 раза
Автокорреляционный прием ОФМн
х(t)= Si(t)+n(t)
0≤t≤T
Fn=![]()
S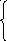
 1(t)= S1(t)=
Si
cos (ω1t)
«1»
1(t)= S1(t)=
Si
cos (ω1t)
«1»
 S2(t)=
-S0(t)
cos (ω2t) «0»
S2(t)=
-S0(t)
cos (ω2t) «0»
Р(S1)= Р(S2)
 х(t)
х(t) 




 а1
i
а1
i
Л







 Ф УПЧ ФНЧ ВУ
УПР ОКП
Ф УПЧ ФНЧ ВУ
УПР ОКП





 t3=T
t3=T

Рош
ортог=0,5
exp
(![]() )
)
РошАК=0,5
exp
(![]() )=0,5
exp[-g]
)=0,5
exp[-g]
РошАК=0,5 exp[-g]
Рош
к=exp
![]() exp[-g]
exp[-g]
Анализ показывает, что АК обработка сигналов с ОФМн для вероятности Рош=(10-6÷10-3) проигрывает в помехоустойчивости когерентной обработки тех же сигналов не более 1,3 дб, поэтому для простых цифровых сигналов благодаря простоте реализации АК приема целесообразно его использовать.
Некогерентный прием простых цифровых сигналов с ЧМн
х(t)= Si(t)+n(t)
0 ≤t≤T
Fn=
≤t≤T
Fn=![]()
S 1(t)= S1(t)=
S0
cos (ω1t+
ω1)
«1»
1(t)= S1(t)=
S0
cos (ω1t+
ω1)
«1»
 S2(t)=
S0(t)
cos (ω2t+
ω2)
«0» i=1,2
S2(t)=
S0(t)
cos (ω2t+
ω2)
«0» i=1,2
![]() Т –
длительность сигнала (бита)
Т –
длительность сигнала (бита)
S
 1(t)= S1(t)=
S0
cos
(ω0t+
φ1)
«1»
1(t)= S1(t)=
S0
cos
(ω0t+
φ1)
«1»
 S2(t)=
S0(t)
cos (ω0t+
φ
2)
«0» i=1,2
S2(t)=
S0(t)
cos (ω0t+
φ
2)
«0» i=1,2
ω1 и ω2 - конкретные значения
Рош
нк=1-Ф
![]()
![]() =
=![]()
![]() S1(t)·
S2(t)dt=
cos (φ
1-
φ
2)
S1(t)·
S2(t)dt=
cos (φ
1-
φ
2)
-1≤![]() <1
<1
cos(φ 1- φ 2)=-1
(φ 1- φ 2)=πk, к=1,3,5,7…
φ1=0
φ2=π для к=1
S2(t)=- S1(t) сигналы противоположны






 1 0
1
1 0
1
 Иi≥h
«1»
Иi≥h
«1»
 Иi≤h
«0»
Иi≤h
«0»
Ui
y



 (t)
(t)
Л





 Ф УПЧ СД ВУ
УПР
Ф УПЧ СД ВУ
УПР


 τ h=0
τ h=0
 СУ
СУ

ЛФ – линейный фильтр
СД – синхр. детектор
ВУ – видеоусилитель
СУ – синхрон.устройство
Р1=Р2 =0,5
Рош
=1-Ф
![]()
Синхронный детектор – недостаток – «обратная работа» (инвертирование произвольная) импульсов инф-ции.
Структуры синхронных детекторов (СД)
Разновидности:
-
Схема Пистелькорса
-
Схема Сифорова
-
Схема Костаса


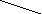

 х ФНЧ
х ФНЧ
1







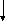
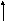











Исп(t)
f0 f0
f0
ФВ
2f0
2f0 f0
f0
2f0
ФВ - фазовращатель
Достоинства:
-
Простота реализации
Недостатки:
-
Низкая помехоустойчивость
-
Явление «обратной работы»:
а) начальная неопределенность
б) влияние умножителя частоты
в) влияние делителя частоты
2









 1 2
1 2
 f0
Иог(t)
f0
Иог(t)

f0 ФВ
 f0
1
f0
1

 2f0
2f0
2f0 f0 2

 2f0
2f0
2 2f0




 ГУН
ГУН





 1
1
ГУН – генератор управляемый напряжением
ФВ – фазовращатель
ФНЧ
Достоинства:
1) Высокая помехоустойчивость
Недостатки:
-
Повышенная сложность
-
Явление «обратной работы»:
а) начальная неопределенность
б) влияние умножителя частоты
в) влияние делителя частоты










1 4








 π/2
π/2



ГУН 2
 3
3

 2
2
Достоинства:
-
Простота реализации
-
Высокая помехоустойчивость
Недостатки:
-
Повышенная сложность
-
Явление «обратной работы»:
а) начальная неопределенность
ОФМн – относительная фазовая манипуляция
Особенности применения квадратурной фазовой манипуляции
Ф Мн
ВPSk
Мн
ВPSk
О ФМн
DBPSk
ФМн
DBPSk
к в.ОФн
QBPSk
в.ОФн
QBPSk
-
Неизменная скорость передачи информации
-
Минимальная полоса частот
-
Неизменная Рош
 1
2 3 4 5 6
1
2 3 4 5 6






аi а1 а2 а3 а4 а5 а6

 t
t




 bi
bi
b1 b2 b3


 t
t




 Ci
Ci
C1 C2 C3

 t
t

![]()
{ai}




 {bi}
{bi}
 X1 cos(ω0t+Ө(t)
X1 cos(ω0t+Ө(t)


 ПИ +
ПИ +

 {ci}
{ci}
X2
ПИ – преобразователь информационного потока {ai} в {bi} и {ci}.
1/![]() sin
(ω0t+π/4)
sin
(ω0t+π/4)
1/![]() bi
cos
(ω0t+π/4)+
1/
bi
cos
(ω0t+π/4)+
1/![]() ci
sin
(ω0t+π/4)=
cos[ω0t+Ө(t)]
ci
sin
(ω0t+π/4)=
cos[ω0t+Ө(t)]
Ө (t) 1800,
±900,
0 – перескок фазы
(t) 1800,
±900,
0 – перескок фазы
Возможны следующие варианты:
b







 i 1
0 1 0
i 1
0 1 0
 сi 1
0 0 1
сi 1
0 0 1


 bi
bi




 1 0 0 1
1 0 0 1


сi 1 1 0 0
 bi
bi




 1 1 0 0
1 1 0 0



сi 1 0 0 1
 bi
bi




 1
0 0 1
1
0 0 1




сi 0 1 1 0
Несущие sin и cos ортогональны
1/![]() sin
w0t
sin
w0t







 X1 ФНЧ
X1 ФНЧ


 Пн аi
Пн аi





 X2 ФНЧ
X2 ФНЧ
1/![]() sin w0t
sin w0t

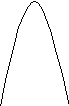 F(w)
F(w)

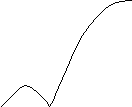 QPSK
QPSK

PSK



w0 2 π/2T 2 π/T w
с имптокомплексная
1/√2 cos
(ω0t+π/4)
имптокомплексная
1/√2 cos
(ω0t+π/4)
с оставл.
оставл.


 bi
bi
 Х
Х
сos(ω0t+Ө(t))

 +
+

 квадратурная
квадратурная
сост. Ci

 Х
Х

1/√2 sin (ω0t+π/4)
1/![]() bi
cos
(ω0t+π/4)+
1/
bi
cos
(ω0t+π/4)+
1/![]() ci
sin
(ω0t+π/4)=
cos[ω0t+Ө(t)]
ci
sin
(ω0t+π/4)=
cos[ω0t+Ө(t)]
Ө (t) 1800,
±900,
0 – перескок фазы
(t) 1800,
±900,
0 – перескок фазы
Возможны следующие варианты:
b







 i 1
0 1 0
i 1
0 1 0
 сi 1
0 0 1
сi 1
0 0 1

b i
i




 1 0 0 1
1 0 0 1



сi 1 1 0 0

 bi
bi




 1 1 0 0
1 1 0 0


сi 1 0 0 1
 bi
bi




 1
0 0 1
1
0 0 1




сi 0 1 1 0
Т.к. sin и cos взаимно ортогональны, то и обрабатывать их можно как два канала:

 1/√2
cos
ω0t
1/√2
cos
ω0t

 bi
bi




 Х ФНЧ
Х ФНЧ


 ПУ аi
ПУ аi



 сi
сi


 Х ФНЧ
Х ФНЧ
1/√2 sin (ω0t+π/4)
B PSK
F(ω)
PSK
F(ω)
QBPSK

Fэф
QBPSK=![]()
Fэф
BPSK=![]()
 ω
2 π/2T
2 π/T
ω
ω
2 π/2T
2 π/T
ω
Достоинства:
-
Возможность умен.полосы канала в 2 раза
Недостатки:
-
Усложняется модель
-
Более высокий уровень ВЧ составляющих сигнала, что приводит к изменению формы огибающей при фильтрации
Вероятность ошибки:
Рош
QBPSK=
Рош BPSK,
т.к.
![]()
Рош
=1-Ф(![]() )
)
Методы повышения достоверности информации:
-
Применение корректирующего кодирования
-
Применение ПС-сигналов
Применение корректирующего кодир.для повышения помехоустойчивости
М – мощность кода
К – количество инф.симв.
n - кол-во симв. в коррект.
r - кол-во добав.сивол.
n = К+ r
Коррект.коды делятся на:
-
Коды, обнаруж.ошибки
-
Коды, исправляющие ошибки
2n – количество возможных комбинаций
М – кол-во разреш.
комбинаций,
![]()
N – кол-во запрещен.комбинаций
Для того, чтобы код был корректирующим, необходимо и дост:
N≥ М
Осн.св-ва:
1) Избыточность
![]() ε=1-
ε=1-![]()
![]() =R0
- относ.скор.передачи информации
=R0
- относ.скор.передачи информации
2) Корректирующая способность
dmin≥a+1 – при обнар. «а» ошибок
dmin≥2a+1 – при испр. «а» ошибок
Если необходимо обнар. «а» ошибок и исправить «в» (при а≥ в)
dmin≥a+в+1
3) Корректир.способность кода связана с оптимизацией r
r≤![]() - нижняя граница Варшамова-Гильберт
- нижняя граница Варшамова-Гильберт
r≥![]() -верхняя граница Хэмминга
-верхняя граница Хэмминга
Оценка потенциальной помехоустойчивости коррект. Кода
n = К+ r
ФМн: Вероятность при посимвольном приеме:
Р01=1-Ф(![]() )
)
К+ r= n
Теперь вероятность ошибки при приеме корр.кода без коррекции:
Р0=1-Ф
![]() ,
если не изменяется R
,
если не изменяется R
Р0>Р01
Пусть коррек. код коррект. ошибки кратности а:
Р0 – вероят.ошибки корр.кода без коррекции
![]() - вероятность
ошибки в кор. Коде кратности q
- вероятность
ошибки в кор. Коде кратности q
Вероятность правильного приема n-a символа в коде:
Р (n-a)пр= (1-Р0) n-a
Вероятность правильного приема корректирующего кода:
Р= Ра 0(1-Р0) n-a
Вероятность правильного приема кода с учетом возможных позиций ошибок кратности а:
Р пр=Саn
Ра
0(1-Р0)
n-a
пр=Саn
Ра
0(1-Р0)
n-a
Сочетания из n по а
Вероятность ошибки при приеме корр. кода с коррекцией:
Рош=![]()
Рош≈![]()
Рош≈![]() - вероятность ошибки одного бита при
приеме коррек. кода с коррекцией
- вероятность ошибки одного бита при
приеме коррек. кода с коррекцией
Чтобы приблизительно (очень грубо) оценить эффективность целесообразности применения корректирующего кодирования:
![]()
К лассификация
лассификация


 Блочные
коды Непрерывные коды
Блочные
коды Непрерывные коды


Систематич. Несистемат
Л
 инейн.
Нелинейн.
инейн.
Нелинейн.
Сверточные коды
