3.Основы теории информации. Количество информации, заключенной в одном дискрете (символе)

a₁, a₂, a₃,… a_м

алфавит сообщения

м -объем алфавита

I (a_i) =f (Р_i)

Р_i – вероятные появления a_i сигнала

Р_i = Р_(ai)

I (a_i , b_j) =f (Р_i)+f(Р_j)=f [P(a_i , b_j)]= f (Р_i Р_j)

Возьмем производную по Р_i

f ¹(Р_i)=P_j f ¹(Р_i Р_j)

P_i f ¹=(Р_i)= P_i P_j f ¹(Р_i Р_j)=K – const

P_i f ¹ =K

f ¹(Р_i)=к/ Р_i

f (Р_i)=Кln Р_i+с с- постоянная интегрирования

Р_i=1 I (a_i)=0

Р_i=0 Кln ₁+с =0

С=0

I (a_i )= Кln Р_i

1= Кln

К=

I (a_i )= log₂ Р_i (бит)

I (a_i1, a_i2,… a_il)= Р_i

3.1 Информационные характеристики дискретных сообщенй

I (А ) – количество информации в фазе, приходящееся на один символ

1) I (А )= (a_i1, a_i2,… a_il) log₂ Р- символы зависимые между собой.

2) Если существует связь между символами a_i и a_j

I (А )= (a_i ,a_j) log₂ Р (бит)

3) Если все символы алфавита взаимонезависимы, то

I (А )= Р_i log₂ Р_i=Н(А) - энтропия источника дискретных сообщений

Н(А) - количество информации в среднем приходящееся на 1 символ алфавита при их взаимной независимости

4) Если символы взаимно независимы и равной вероятности появления, то

Н_max (A)= log₂ m – максимальная энтропия

m – объем алфавита

5) =1-

относительная скорость передачи информации

При прохождении канала связи КС:

А

a_i канал b_j j=I, m

связи

i=I,m B

n (t)

КС:

1. Симметричные и несимметричные

2. С памятью и без памяти

Наиболее характерные КС – несимметричные без памяти КС

6) взаимное количество информации в среднем на один символ на выходе КС:

I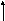 (А; В )= Н(А )-Н (А/В )= Н (В )-Н (В/А )

условная энтропия

I (А; В)= Н(А )-Н (А/В )= Н (В )-Н (В/А )

Н(А ) – это источники сообщения

Н(В )= (b_j ) log₂ Р(b_j)

если канал связи симметричный без памяти:

m=m¹

Р(b_j) = (a_i ,a_j)= (a_i) Р (b_j/ a_i )

Условная энтропия – количество информации в среднем приходящийся на искаженный символ

Н (А/В )= (a_i , b_j) log₂ Р(a_i , b_j)

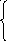Н (В/А )= (a_i)· Р (b_j/ a_i )log₂ Р (b_j/ a_i )

Р (b_j/ a_i )= Рош, i ≠ j

1 – Рош= Рпр, i = j

Н (А ) кодирование источника сообщения неравномерное

Н_макс (А ) равномерное кодирование

3.2 Скорость передачи информации, пропускная способность дискретного канала связи

П_и – производительность источника

П_и==V_n· Н(А ) (бит/с)

V_n – скорость передаваемых символов (cим/c)

(количество символов в единицу времени)

Н(А ) – энтропия

В канале без помех:

R=П_и= V_n· Н(А )= Н(А ) (бит/с)

V_n = 1/Т_с

Т_с - длительность символа

R – скорость передачи информации

R _макс=С_к= V_к· Н_макс(А) (бит/с) – максимальная скорость передачи информации в КС

С_к – пропускная способность дискретного канала связи

R=[Н(В)-Н(В/А)] (бит/с)

С_к =[Н_макс(В)-Н(В/А)] (бит/с)

Н_макс(В)= log₂ m= Н_макс(А) – для симметричного канала связи без памяти

a₁ , a₂ m=2 («0» и «1»)

Н(А ) = Р_j log₂ Р_i =Р(a₁) log₂ Р(a₁) - Р(a₂) log₂ Р(a₂)=

= Р₁ log₂ Р₁ –(1- Р₁) log₂ (1- Р₁)

H(A)

Н_макс=1

Для бинарного канала с помехами:

R =1/ Т_с [- Р₁ logР₁-(1-Р₁) log₂ (1-P₁)+ Р_oш log₂ Р_ош+(1-Р_ош) log₂ (1-P_ош)]

Н (В/А )= (a_i)· Р (b_j/ a_i )log₂ Р (b_j/ a_i ) = Р_oш log₂ Р_ош-(1-Р_ош) log₂ (1-P_ош)

пропускная способность канала

С_к [1+ Р_oш log₂ Р_oш +(1-Р_ош) log₂ (1-P_ош)]

Если m>2

Н (В/А )= (a_i ) Р(b_j/ a_i ) log₂ Р (b_j/ a_i )=-(m-1) Р_oш log₂ Р_oш –

-(1-Р_ош) log₂ (1-P_ош)

3.3 Количество информации передаваемой непрерывным сообщением

Х(_t) – непрерывное сообщение как случайный процесс

Р(х) – плотность распределения Х(_t)

х₁, х₂, ….. х_m

t₁, t₂, ….. t_m

∆= t_i- t_i-1

В соответствии с теоремой Котельникова

∆= (n=2+8), - верхняя граничная частота

х_i=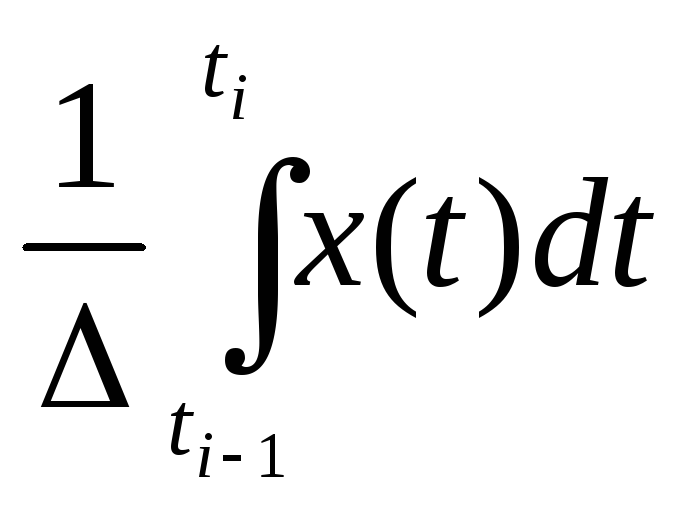

х_i P_i=P(x_i)= P(x_i)· ∆ x, ∆ x – ошибка измерения.

x_i – усредненное значение амплитуды

I (x)= P(x_i) · ∆ x_i log₂ Р ( x_i)· ∆ x_i= P(x_i) · ∆ x_i log₂ Р ( x_i)-

∆ x_i log₂ ∆ x_i = P(x_i) · ∆ x_i log₂ Р ( x_i)- log₂∆ x_i

I₁(x)=lim I (x)=- P(x) log₂ Р (x)dx- log₂∆ x

∆ x_i 0

m ∞

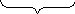1) I₁(x)=- P(x) log₂ Р (x)dx- log₂∆ x (бит)

h (x)

дифференциальная энтропия источника непрерывных сообщений

h (x) – это количество информации в среднем приходящееся на одну выборку непрерывного сообщения

∆ x – ошибка

2) h_макс (x)= log₂

P(x)=lxp

m_x – мат.ожидание

X (x(t)) КС У(у(t))

n(t)

y(t) = x(t)+ n(t)

I(x;у)= h (x)- h (x/у)= h (у)- h (у/x)

h (у/x)= _- P(x, у) log Р (у/x) dx dу- условная диф. энтропия - количество информации в среднем приходящейся на выборку шумового случайного процесса

Если n(t) – нормальный случайный процесс, x(t) – норм.случ.процесс, то и у(t) – будет нор.случ.процесс

Если n(t) σ²_n

x(t) σ²_x

y(t) σ²_y

σ²_y= σ²_x+ σ²_n

h (у/x)= log₂

h (у)= log₂

I(x,у)= log₂- log₂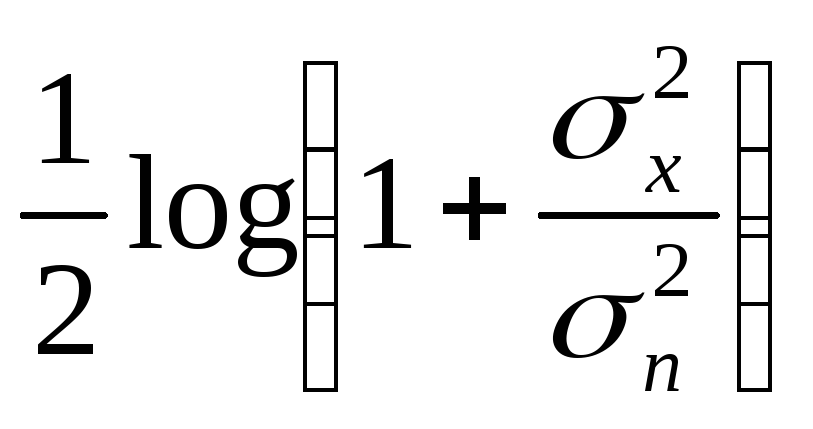₌(бит/с)