
- •Космические
- •1.Обобщенная структурная схема одноканальной рспи
- •Корреляционная функция
- •3.Основы теории информации. Количество информации, заключенной в одном дискрете (символе)
- •3.1 Информационные характеристики дискретных сообщенй
- •3.2 Скорость передачи информации, пропускная способность дискретного канала связи
- •3.4 Скорость передачи информации, пропускная способность канала связи при передачи непрерывных сообщений
- •4. Оптимальные приемники в системах передачи цифровой информации
- •Сверточные коды в рспи
- •Декодирование ск
- •2.Б) Бессиндромное декодирование ск:
- •Применение пс-сигналов в системах передачи цифровой информации
- •Когерентный прием пс-сигналов с дфМн и ортогонал.Информац.Модуляцией
- •Особенность некогерентного приема пс-символов
- •Быстрый поиск
- •Оценка времени поиска псп (последовательный метод поиска)
- •Применение ансамбля пс сигналов для передачи цифровой информации
-
Корреляционная функция
АКФ одиночной (апериодической) М-последовательности
R
 (
(![]() )
=
)
=![]() S
(t)
S (t-t)dt
S
(t)
S (t-t)dt
аi i=1,N
R (n
τ
o+ε)=![]()
n=0, 1, 2…N
0≤ ε≤ τ o, τ o - длительность одного символа
ρ (τ)=![]() - нормированная АКФ.
- нормированная АКФ.
ρ (0)=1 для всех сигналов
ρ (τ)<1

 τ ≠0 1,
τ ≠0 1,
![]() =0
=0
ρ (τ) = ≤
(τ) = ≤![]() ,
,
![]()
ρn
(n
τ 0)
=
![]() аi
аi+n
аi
аi+n
п ериодическая
нормированная решетчатая АКФ.
ериодическая
нормированная решетчатая АКФ.
![]() 0<( τ) ≤ τ
0
0<( τ) ≤ τ
0
ρn (τ) = -1/N, другие значения τ
-
Спектр
S(jω) – спектральная функция
F(ω)=![]() - спектральная плоскость
- спектральная плоскость
![]()
![]() =
=![]() ·
еjφ(ω)
·
еjφ(ω)
![]() =
=![]() ·
е-jφ(ω)
·
е-jφ(ω)
F(ω)=
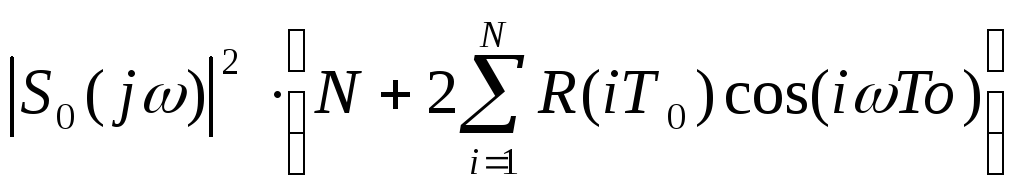
Fп(ω)=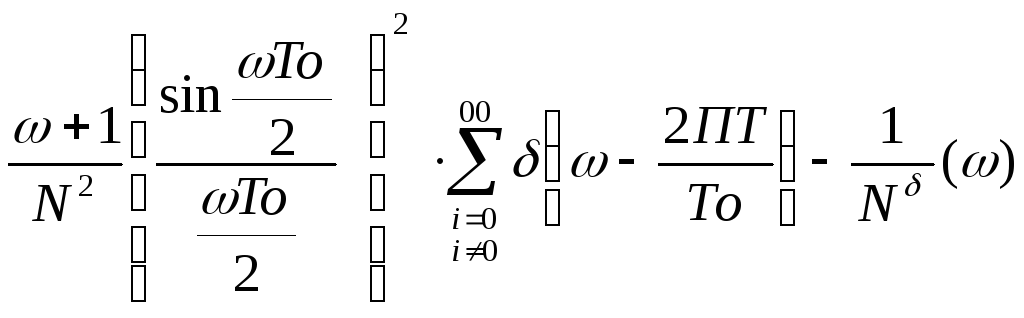
2.1.2 Четвертичное кодирование последовательности (ЧКП)
ПСП-нелинейные
-
Значность
N=2, К=2,3,4,5…
-
Z
 =N
=N
Количество одной значности
3) Формирование
Алгоритмический и аналитический способ формирования
А лгоритмический
способ
лгоритмический
способ
А кi=
где
ai
,
,
i=
1, N
кi=
где
ai
,
,
i=
1, N
i= 0,1,2,…N-1
к =3
А03,
А13,
А23,
А33,
А43,
А53,
А63,
А73,
=3
А03,
А13,
А23,
А33,
А43,
А53,
А63,
А73,
Способ по алгоритму:
1) i представляется в «к» разрядной двоичной форме
к =3
i=6 110
=3
i=6 110
 1 001
1 001
 0 000
0 000
2) Если 1 разряд двоичного номера
« 0» 11
0» 11
« 1»
10
1»
10
Если 2 разряд двоичного номера и все последующие
 0» 1110
(и все последующие)
0» 1110
(и все последующие)
« 1»
1101
1»
1101
Если 3 разряд двоичного номера «0»
 0» 11011110
0» 11011110
« 1»
11100010
1»
11100010
А
 53 101 10110111
53 101 10110111
А
 03 000
11101101
03 000
11101101
Аналитический способ:
Акi=![]()
![]()
 - функция Радемахера
(мгандровые функции)
- функция Радемахера
(мгандровые функции)
Скi – значение i – го разряда двоичного номера последовательности
С1=1, С2=1, С3=1
Т






 U 1 2 3
U 1 2 3










 В1
В2 В3 1
В1
В2 В3 1




& &









 1р
1р
В1






 2р
2р
В2





В3



& 3р
4) ∆ - разность между символами «0» и «1» одиночной последовательности
∆=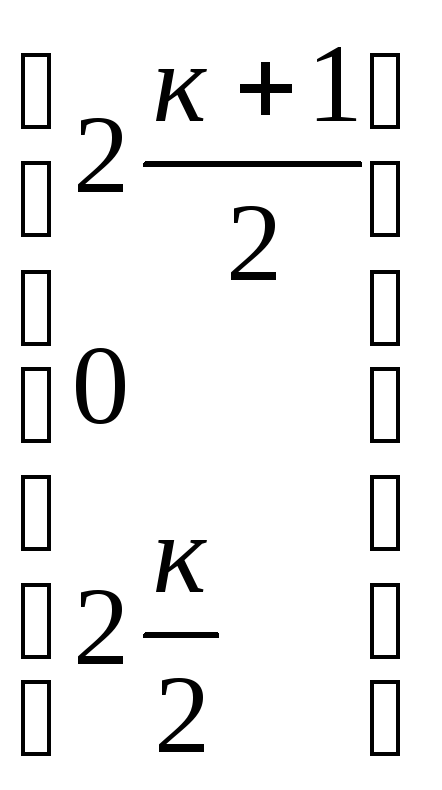 к
– нечетное
к
– нечетное
к - четное
5) Каждое ЧКП Акi
соответствует ей парная Аiк,
причем
![]()
У парной последовательности первая половина символов совпадает, вторая – противополпжные
А13 и А53
А
 13 001 10111000
13 001 10111000
А
 53 101 10110111
53 101 10110111
-
Каждой ЧКП Акi соответствует ей смежная Аiк
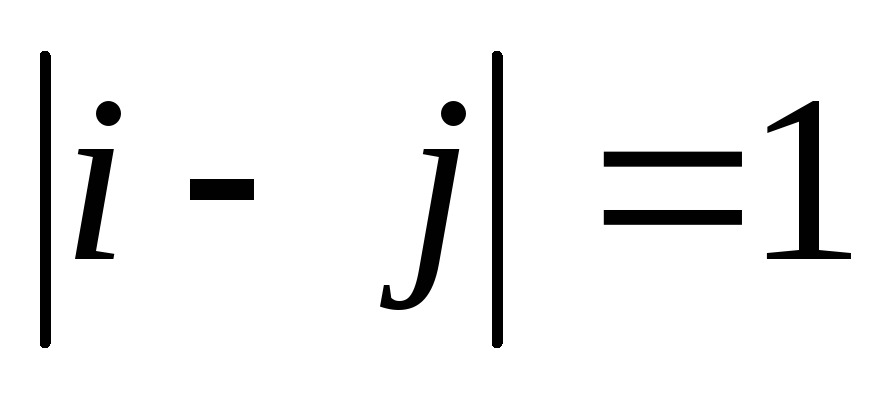
У смежных последовательностях символы, стоящие на нечетных позициях совпадают, а на четных – противоположны. А13 и А53
А
 03 000 11101101
03 000 11101101
А
 13 001 10111000
13 001 10111000
-
Корреляционные свойства
А КФ
0≤ (τ)
≤ τ 0
КФ
0≤ (τ)
≤ τ 0
ρ(τ)=
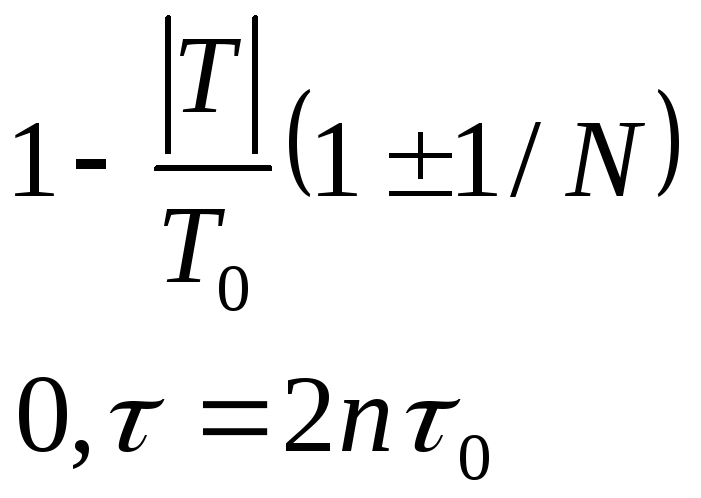 n=1,2,3…
n=1,2,3…
![]() ,
др.знач. τ
,
др.знач. τ
где
![]() - длительность
символа последов.
- длительность
символа последов.






![]()











 Т/
Т/![]()
1 2 3 4 5 6 7 8 9 10
ρ(τ)=
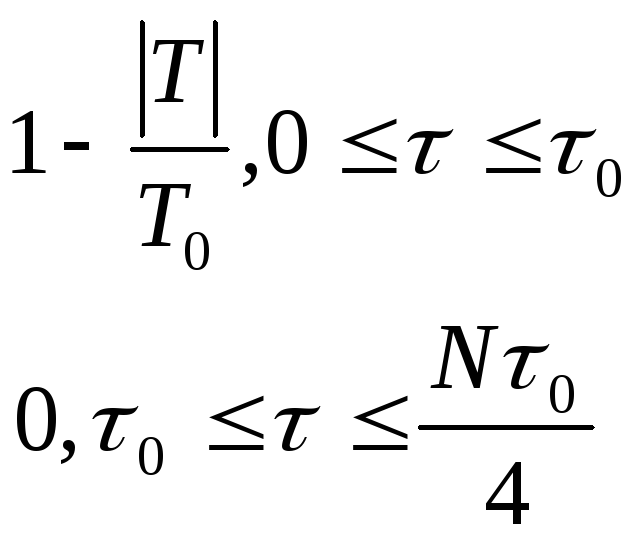 для одного периода
для одного периода
![]() ,
,
![]() ≤
τ ≤ 3N
τ 0/4
≤
τ ≤ 3N
τ 0/4
0, 3N τ 0/4≤ τ ≤(N-1) τ 0
ρ(τ)





 1
1



N τ 0
ВКФ – взаимокорреляционная функция:
У последовательности одной значности
Ρij(τ)
![]() ,
,
i ≠j
Для последовательности одной значности:
Ρij=0, т.е. ансамбль последовательности одной значности ортогонален.
А
 03 000 111-111-11
03 000 111-111-11
А
 37 111
37 111 ![]()
![]()
-
Свойства дополнительной серии
Дополнительной серией называется пара цифровых последовательностей одной значимости, у которых боковые остатки АКФ имеют равные по абсолютной величине значения и противоположны по знаку.
Смежные и парные ЧКП образуют дополнительные серии
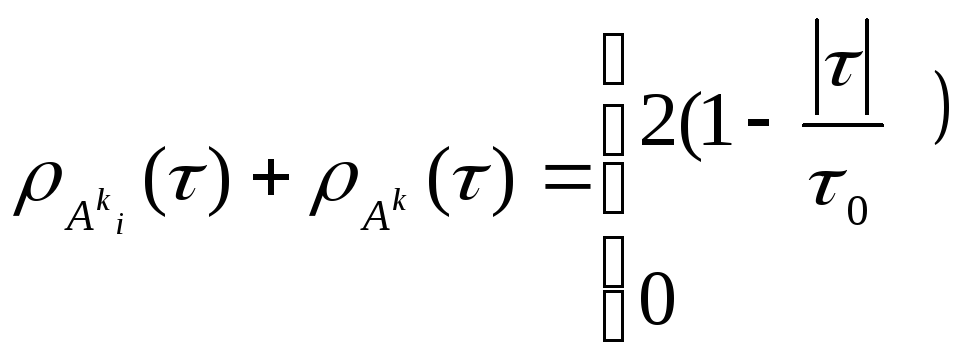 др. знач.τ 0≤ τ
≤ τ 0
др. знач.τ 0≤ τ
≤ τ 0
 др. знач.τ 0≤ τ
≤ τ 0
др. знач.τ 0≤ τ
≤ τ 0
9) Спектр
F (ω)=
(ω)=
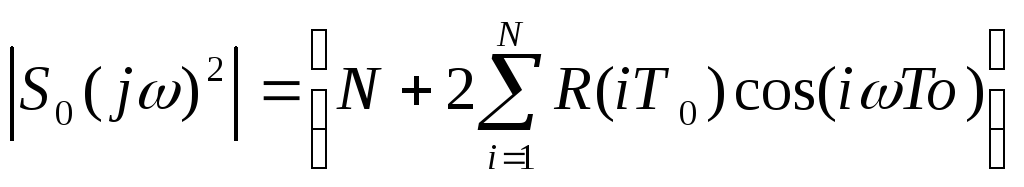
F(ω)























 ω
ω

![]()
![]()
2.2 ПС сигналы с дискретной частотной модуляцией
Это сигналы, имеющие N дискретных частот с минимальным разносом
∆F=1/ τ 0
τ 0 – длительность элементарного дискрета
Частоты в сигнале (f1, f2,… fN) следуют по закону случайных чисел.
S
 (t)=
(t)=![]() rect [t-(i-1) τ
0]ехр
-j [w0t+(Ni-Nп)·2T∆F
τ
0+φ0]
rect [t-(i-1) τ
0]ехр
-j [w0t+(Ni-Nп)·2T∆F
τ
0+φ0]
г де
Ni-
номер числовой последовательности
де
Ni-
номер числовой последовательности
Nп= ![]() N
– четные
N
– четные
N - нечетные
Дискретные символы в ДЧМ сигнале взаимно ортогональны, благодаря разносу по частоте
Тс=N τ 0
N – количество дискретных частот (элементарный дискрет0
Т

 с
- длительность сигнала
с
- длительность сигнала
![]() - длительность элементарного дискрета
- длительность элементарного дискрета
fi , i=1,N
![]()
![]() =0,2
(N+1)
– Диофантового уравнения дает случайную
последовательность чисел.
=0,2
(N+1)
– Диофантового уравнения дает случайную
последовательность чисел.
С
ТИ












 1 2 3
1 2 3
+




 аi
аi
Сигналы:
а) с когерентной сеткой частот (φ1= φ2=…= φN)
б) с некогерентной сеткой частот (φ1≠ φ2≠…≠ φN)
Основные свойства
1) Тс=N τ 0
2) Z=(N-1)! количество сигналов одной значности (длительности)
3) В=Тс·Fэф - база сигнала
Fэф= N/ τ 0
В= N τ 0· N/ τ 0= N2=К
4) Корреляционная функция сигнала:
а) все сигналы ансамбля взаимно ортогональны
б )
АКФ
)
АКФ
ρ(τ)=
![]()
![]()
![]()

Fэф=N/ τ 0
Достоинства ДЧМ:
-
Высокий коэффициент сжатия
-
Большой ансамбль взаимоортогональных сигналов (повышается помехозащищенность и скорость сигнала)
-
Все сигналы ансамбля одной значности взаимоортогональны
-
Кнопочный вид АКФ
-
Спектральная плотность сигнала примерно одинакова в пределах Fэф.
Недостатки:
-
Сложность формирования ДЧМ
-
Сложность когерентной обработки такого сигнала
