Введение

Информация- это совокупность сведений о различных объектах, явлениях, процессах, предназначенных для передачи информации из одной точки в другую.

Сообщение – это информация, представленная в определенной форме.

Сигнал – это носитель информации.

Виды сообщений:

1. Непрерывная функция времени - λ (t), (λ_min, λ_mах).

2. Дискретная функция - λ₁, λ₂,…λ_m

3. Функция от координаты (одной или несколько) - λ (х), λ (х, у), λ (х, у, z)

4. Пространственно-временная функция - λ (х, у, z, t)

РСП с непрерывным изучением

РСП с дискретным

Радиоканалы:

1. Ионосферный

2. Тропосферный

3. Метеорные

4. Космические

Канал с постоянными параметрами.

Канал с переменными параметрами.

По назначению:

1. Телеметрические

2. Связные

3. Передачи данных

4. Космические

В зависимости от источников и потребителей информации:

1) Одноканальные РСПИ

2) Многоканальные РСПИ

3) Многостанционные

1.Обобщенная структурная схема одноканальной рспи

Z S^*(t) СУ

λ(t) U(t) Uк(t) S(t) U^*к(t) U^*(t)

ИИ ЭП КУ М ВЧ ВЧ ДМ ДКУ ОЭП

РК

помехи λ^*(t)

n(t) ПИ

C ГН

потр. инф.

Рис.1

ЭП – электрофизический преобразователь

ИИ – источник информации

КУ – кодирующее устройство

М – модулятор

ГН – генератор несущий

С – синтезатор опорных частот

ВЧ – высокочастотная часть

Оценка сигнала

S^*(t)=µ S(t)+ n(t)

ДМ - демодулятор

ДКУ – декодирующее устройство

ОЭП – обратный электрофизический процесс

СУ – синхронизирующее устройство

ПИ - потребитель информации

Ошибка сообщения

Е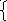 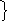(t)= λ(t) - λ^*(t)

S(t)= l _эп· l _ку· l _м λ(t)

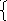
λ ^*(t)= l _эм· l _дДКУ· l _ОЭП µ S(t)+ n(t)

2.Сигналы в РСПИ.

Виды сигналов:

1. Сигнал как функция времени

2. Аналитическая функция

3. Спектральная функция

4. Дискретная функция

5. Геометрическое представление

Основные характеристики:

1. Длительность сигнала (время анализа τ)

2. Эффективная полоса частот сигнала Fэф =

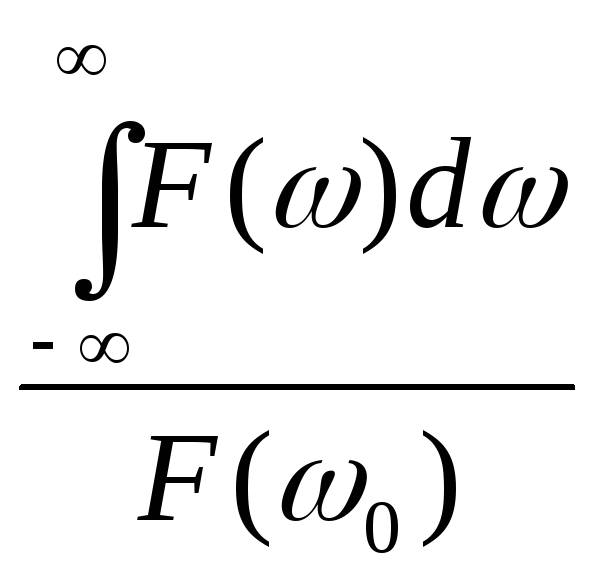
3. Вид информационной модуляции (АМ, ЧМ, ИМ: АИМ, ШИМ, ВИМ, НИМ)

4. Корреляционная функция

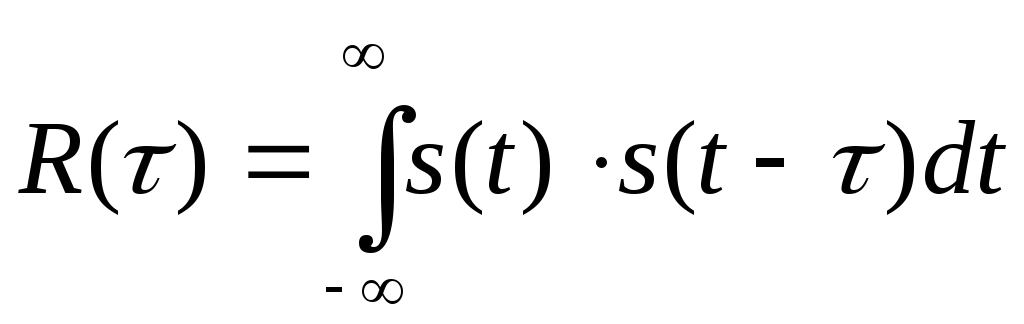
R(0) = E

R(-) = R()

5. База сигнала

6. Мощность, энергия сигнала

,

Простые сигналы В≈1

Сложные сигналы В>>1

В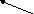= Fэф· с – база сигнала

эффективная полоса длительность сигнала

Сложные сигналы – псевдослучайные (ПС) (шумопододные) – это сигналы, которые по своим статистическим характеристикам приближаются к случайным сигналам, но по природе детерминированные.

Свойства сигналов:

а) Взвешенность – это сигнал, у которых математическое ожидание близко к нулю.

S(t) м_s=<s(t)>≈0

б) Кнопочный вид автокорреляционной функции

S(t) R(t)=S(t) · S(t-t) dt – АКФ сигнала

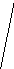
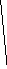R(о)

R(о)=Ес

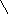
∆ ∆<<R(о)

в) Постоянство спектральной плотности в полосе Fэф.

ПС-сигналы

1. ПС – сигналы с дискретной фазовой модуляции (ДФМ)

2. ПС-сигналы с дискретный частотный модулятор (ДИМ)

Достоинства РСПИ с ПС сигналами:

1. Повышение помехозащищенности

2. Повышается информационная защищенность сигнала

(скрытность)

структурная

(криптографическая) энергетическая

нелинейность

формирования широкополостность

3. Возможность построения многоадресных систем. ПИ (передачи информации)

4. Возможность повышения скорости передачи информации

Основное достоинство ПС-сигнала - это способность их сжиматься или во времени, или по частоте

Коэффициент сжатия равен базе

2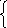.1 ПС сигналы с ДФМ (дискретной фазовой модуляцией)

S(t)=rect [t-(i-1)] exp j [w₀t+φ_i+ φ₀]

где φ_{i ,} i= I, N - принимает значение по псевдослучайному закону

I, (i-I)t₀ ≤t≤it₀;

rect [t-(i-1)]=

единичн.функция О, др.значен.t;

t₀ – длительность элементарного дискрета;

φ₀ – известная начальная фаза.

S(t)=rect [t-(i-1)]cos (w₀t+φ_i+ φ₀)

S(t)= cos φ_i rect [t-(i-1)]cos (w₀t+φ₀)

cos φ_i=a_i

S(t)= a_i rect [t-(i-r₀]cos (w₀t+φ₀)

где a_i , _, i= I, N

U(t)= a_i rect [t-(i-1)] -ПСП -псевдослучайная последовательность

ПС-сигнал – гармоническое колебание, параметры, которые модулируются (один или несколько) по 3-му закону ПСП.

ПСП:

а) двухуровневые (двухфазные)

б) многоуровневые (многофазовые)

S(t)

ГОС ГПСП ФМ

ГН

Рис.2

ГОС – генератор опорных сигналов

ГПСП – генератор псевдослучайных последовательностей

ФМ – фазовый модулятор

ГН – генератор несущей

Для 2 уровней сигнала

φ_i=0, φ₂=П

а_i=1, а₂=-1

Классы ПСП:

а) м – последовательности,

б) четвертично кодированные (ЧКП)

2.1.1 М-последовательности:

М – последовательности – это линейные рекуррентные последовательности максимального периода, которые описываются неприводимыми и примитивными полиномами вида

Со+С₁х+ С₂х²+… С_кх^к

С_о, С₁, …С_к - коэффициенты равные либо 0, либо 1

На основе полинома строится рекуррентная формула:

а_i= а_i-3а_i-1 (а_i= 0, 1 )

Свойства М-последовательности:

1) Значность (или количество символов в одной последовательности)

N=2^к-1

К – максимальная степень генераторного полинома

2) В М-последовательности присутствуют все комбинации двоичных символов по «К»

3) Количество единиц на единицу больше количества нулей (свойство взвешенности)

4) Если данную М-последовательность (в двоичной форме) сложить по модулю 2 с ее сдвигом, что получим ту же М-последовательность, но с другим циклическим сдвигом

1110010

сдвиг 2 разр. 1001011

0111001 - исходные со сдвигом на один символ вправо

5. Количество М-последовательностей одной значимости – Z

K	3	4	5	6	7	8	9	10
Z	2	2	6	6	18	6	48	60

Z=

φ(x) – функция Эйлера

φ(x) –это количество целых положительных чисел меньших N и взаимопростых с N, в том числе «1»