
- •1) Понятие тока, напряжения, сопротивления, емкости, индуктивности. Основные зависимости в схемах. Закон Ома, законы Кирхгофа. Параллельное и последовательное соединение элементов.
- •Первый закон
- •Второй закон
- •Последовательное соединение
- •Параллельное соединение
- •2) Представление сигналов в частотной и временной областях. Спектр, ачх, фчх, вах (примеры). Виды сигналов. Единицы измерения частот и амплитуд. Понятие частотной фильтрации.
- •Классификация сигналов
- •3) Диод: принцип работы, характеристики, схемы включения. Участки вах диода и их зависимости. Схема выпрямителя: описание работы и назначение схемы.
- •5) Усилитель на биполярном транзисторе, схема и назначение элементов.
- •6) Операционный усилитель: принцип работы, характеристики, основные зависимости.
- •7) Принцип работы и схемы включения операционного усилителя.
- •Основы функционирования
- •Простейшее включение оу
- •8) Генератор стабильного тока: описание работы гст, описание работы схемы.
- •9) Полевой транзистор: описание работы, характеристики, схемы включения.
- •10) Схемотехническая реализация устройств флеш-памяти на полевых транзисторах с плавающим затвором. Основные принципиальные схемы флеш-памяти.
- •11) Двоичная система счисления. Законы двоичной логики. Простейшие логические элементы: принцип работы, условные графические обозначения.
- •12) Законы двоичной логики. Схемотехническая реализация элемента «не»: описание работы схемы.
- •16) Триггерные устройства: назначение, принцип работы. Схемотехническая реализация и принцип работы rs-триггера, синхронного rs-триггера, d-триггера.
- •17) Триггерные устройства: назначение, принцип работы. Схемотехническая реализация и принцип работы jk-триггера и синхронного rs-триггера.
11) Двоичная система счисления. Законы двоичной логики. Простейшие логические элементы: принцип работы, условные графические обозначения.
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).
Запись двоичных чисел
Двоичная система счисления является частным случаем сдвоенных двоичных показательных позиционных систем счисления с обоими основаниями (a и b) равными 2. Целые числа записываются в виде:
![]()
где:
![]() —
представляемое
число,
—
представляемое
число,
![]() —
запись
числа, строка цифр и знаков,
—
запись
числа, строка цифр и знаков,
![]() —
число цифр (знаков)
в числе x2,2,
—
число цифр (знаков)
в числе x2,2,
![]() —
порядковый
номер цифры,
—
порядковый
номер цифры,
![]() —
цифры
числа x2,2 из
множества a={0,1},
весовые коэффициенты, в двоичной системе
счисления основание внутриразрядной
системы счисления равно 2,
—
цифры
числа x2,2 из
множества a={0,1},
весовые коэффициенты, в двоичной системе
счисления основание внутриразрядной
системы счисления равно 2,
![]() —
основание
показательной весовой функции, основание
межразрядной системы счисления.
—
основание
показательной весовой функции, основание
межразрядной системы счисления.
Целые числа являются частными суммами степенного ряда:
![]()
в
котором коэффициенты an берутся
из кольца R=a{0,1}, X=2, n=k,
а верхний предел в частных суммах
ограничен с ![]() до — n-1.
до — n-1.
Основание показательной функции — b определяет только диапазон представляемых числами x2,b величин. Число записываемых кодов от основания показательной функции - b не зависит. Число записываемых кодов зависит от основания внутриразрядной системы счисления - a, определяется в комбинаторике и равно числу размещений с повторениями:
![]()
где a=2 — 2-х элементное множество a={0,1} из которого берутся цифры ak, n — число элементов (цифр) в числе x2,b.
Дробные числа записываются в виде:
![]()
где:
![]() —
число
цифр дробной части числа,
—
число
цифр дробной части числа,
![]() —
весовые
коэффициенты из множества
—
весовые
коэффициенты из множества ![]() ,
основание внутриразрядной системы
счисления равно 2,
,
основание внутриразрядной системы
счисления равно 2,
![]() —
основание
показательной весовой функции, основание
межразрядной системы счисления.
—
основание
показательной весовой функции, основание
межразрядной системы счисления.
Следует отметить, что число может быть записано в двоичном виде, а система счисления при этом может быть не двоичной, с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
12) Законы двоичной логики. Схемотехническая реализация элемента «не»: описание работы схемы.
1. Закон тождества Истинное решение любой корректно поставленной задачи в одной системе отсчета (что очень важно) одно, а не 2 и не 10. математически это выглядит так: 2+3=5 и никак иначе. если ответов истинных больше, то либо вопрос был задан не корректно либо ответ получен для нескольких систем. Теперь воспользуемся частным случаем, а именно, наблюдением за работой любой булевской функцией. Все они дают ОДНОЗНАЧНЫЙ ответ, либо 1 либо 0, на любые возможные комбинации на входе. 2. Закон противоречия Закон противоречия говорит о том, что если одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте, в одно и то же время и в одном и том же отношении, то они не могут быть одновременно истинными. (т.е. этот закон также действует для одной системы отсчета, в которой и рассматриваются аргументы) Теперь посмотрим, как он выглядит, наблюдая за частным случаем, а именно за физической работой базового логического элемента булевой логики. Если на выходе логического элемента присутствует лог. 1, то в то же самое время, на нем не может быть лог. 0. Т.е. дно исключает другое. 3. Закон исключенного третьего (область применения которого также одна система отсчета) Рассмотрим закон исключенного третьего на работе того же базового логического элемента. На выходе логического элемента присутствует либо 1 либо 0, и третьего не дано. Лог."1" и лог "0" в системе отсчета "схема" имеет содержание. Обычно, логические уровни 1, это 5 вольт, а "0" имеет значение отличное от нуля, но не превышающее 10% от напряжения питания логического элемента. В системе отсчета "схема" может иметь место быть пограничное напряжение, которое входной измеритель (который присутствует на входах каждого логического элемента) не может интерпретировать однозначно, в результате чего в схеме возникает ошибка, или, как ее называют "логические гонки". Следствием такой ошибки, практически всегда является колебательный процесс, или генерация логического элемента (возбуждение). При этом логический элемент признается не работоспособным, а информация с его выхода становится не объективной и не может быть использована в следующих частях схемы. Как видим, несоблюдение закона исключенного третьего, ведет на этом примере к появлению совершенно нового состояния логического элемента. т.е. третье состояние принадлежит уже не статичной СО, а динамической ИСО. Но смысл в том, что третье возможно, но в другой системе отсчета. 4. Закон достаточного основания (мультисистемный, т.е. означает, что это общий принцип для всех систем отсчета) Рассмотрим этот закон на примере нормально физического функционирования базисного булевского элемента: На выходе инвертора имеем лог "1", это означает, что необходимым и достаточным основанием для этого, является наличие на его входе логического "0".Конечно, причиной появления на выходе инвертора может служить и другой фактор, например, короткое замыкание выхода на плюсовую питающую шину.Но, это уже будет иметь отношение к другой системе отсчета "схеме", а не к системе отсчета "логический элемент инвертор". Ситуация повторяет ситуацию с законом исключенного третьего, и тоже это упущение Аристотеля о том, что область применения этого закона касается только одной системы отсчета, явилась основанием для спекуляций и неправильного применения этого закона.
Логический элемент, который мы добавим в схему робота, называется элемент "НЕ", или "инвертор". Инвертор имеет один вход и один выход. Когда на вход инвертора подается логическая "1" (логическая единица - сигнал высокого уровня), то на выходе мы будем иметь логический "0" (логический ноль - низкий уровень сигнала), а когда на вход будет подан логический "0", то на выходе будет присутствовать логическая "1".
|
|
|
|

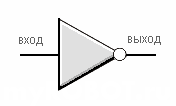 Обозначение
элемента "НЕ" в американском
стандарте ANSI (American National Standart Institute -
американский национальный институт
стандартов).
Обозначение
элемента "НЕ" в американском
стандарте ANSI (American National Standart Institute -
американский национальный институт
стандартов).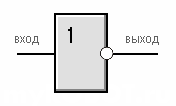 Обозначение
элемента "НЕ" на схемах по
российскому ГОСТу и европейскому
стандарту DIN (Deutsche Ingenieuring Normen - немецкий
инженерный стандарт). Иногда цифру
"1" внутри элемента не ставят для
простоты.
Обозначение
элемента "НЕ" на схемах по
российскому ГОСТу и европейскому
стандарту DIN (Deutsche Ingenieuring Normen - немецкий
инженерный стандарт). Иногда цифру
"1" внутри элемента не ставят для
простоты. Таблица
истинности для логического элемента
"НЕ".
Таблица
истинности для логического элемента
"НЕ".