Теорема
Пусть функция
определена и дифференцируема на отрезке
,
причем все ее значения
.
Пусть кроме этого,
при
(3)
Тогда итерационный процесс сходится и
дает в пределе единственный корень
уравнения
Доказательство:
Уравнение
имеет на отрезке
действительный корень. Обозначим его
ξ
Выбираем произвольные
и
строим итерационную последовательность
;
;…;
.
Рассмотрим уравнение
.
(*)
Т.к. (
-
корень уравнения
,
т.е.
,
а
).
Применяем теорему Лагранжа к уравнению (*).
,
где
лежит между
и
,
т.е.
.
Согласно неравенству (3), имеем
,
т.к.
.
Аналогично находим
Используя следующее неравенство, получаем
Повторяя процесс, получаем
(4)
По условию теоремы
,
поэтому из (4) следует
,
т.е.
.
Т.е. итерационная последовательность
сходится и дает в пределе корень уравнения
.
Корень этот единственный.
Действительно, предположим, что на этом
отрезке есть еще корень уравнения
.
Тогда
т.к.
.
Пришли к противоречию. Теорема доказана.
Замечание 1. По условию
теоремы итерационный процесс сходится
при любом выборе
.
Благодаря этому он является
самоисправляющимся, т.к. неверно
вычисленное
можно рассматривать как новое нулевое
приближение.
Замечание 2.
,
Т.к.
,
,
то каждое последующее приближение ближе
к корню чем предыдущее.
Геометрический смысл метода итераций.
К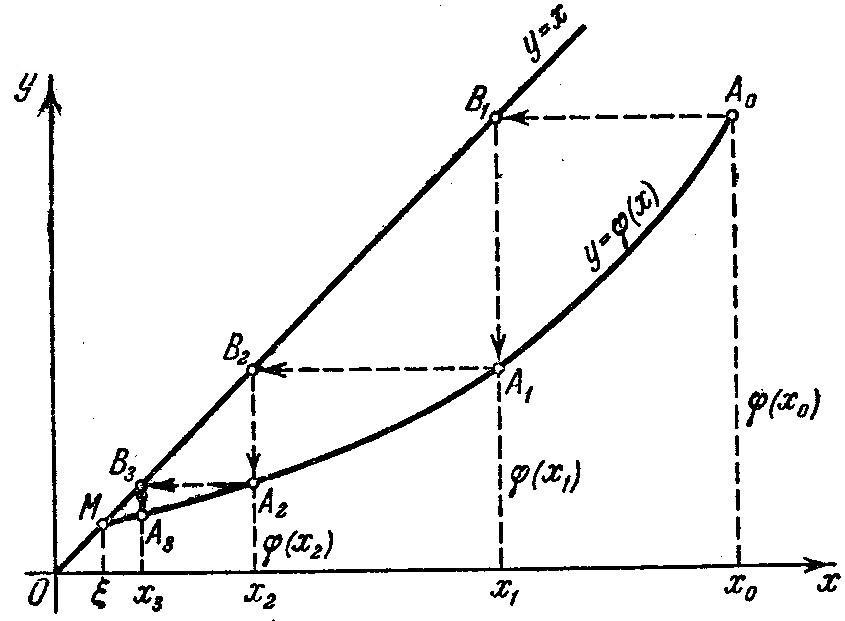
орень
уравнения
-
это абсцисса точки пересечения кривой
и
прямой
.
а) При
приближения
и т.д. монотонно убывают, приближаясь к
(или возрастают, если
).
Условие теоремы
,
автоматически выполняются если
.
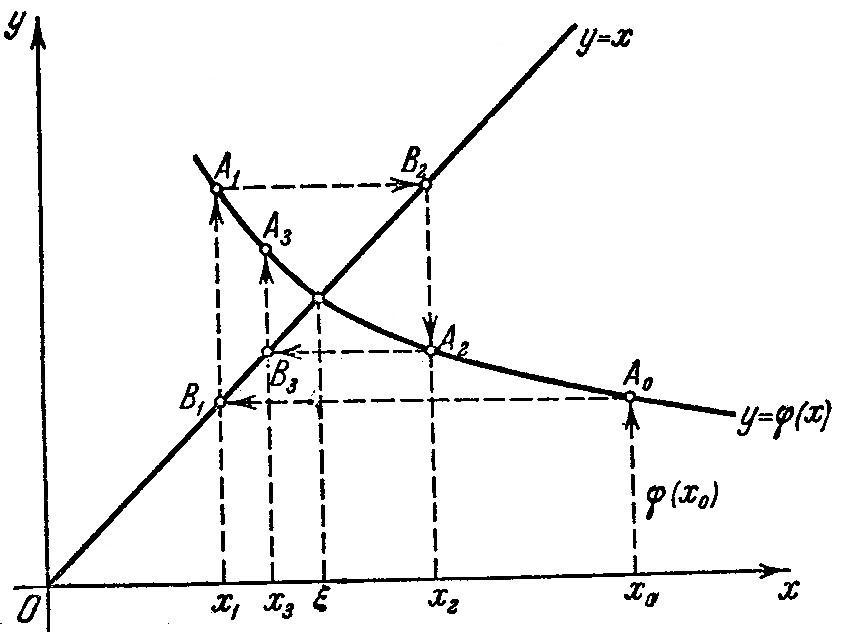
б) При
последовательные приближения колеблются
около
.
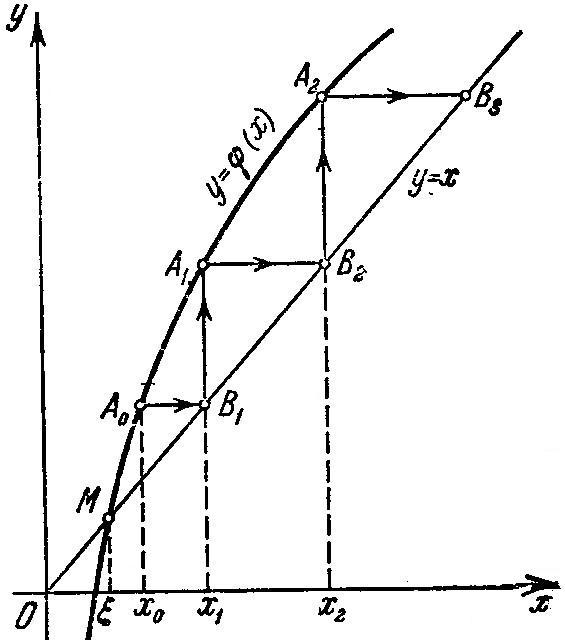
в) При
итерационный процесс расходится!
Для применения метода итераций уравнение
нужно привести к виду
так, чтобы
при
.
Это можно сделать различными способами:
1. Уравнение
заменяется равносильным
.
В этом случае
.
Параметр подбирают так, чтобы
,
при
.
2. Уравнение
заменяется равносильным
,
где
-
произвольная, дифференцируемая на
отрезке
функция, не имеющая корней на отрезке
.
подбирают так, чтобы
,
при
.
Можно показать, что при соответствующем
выборе функции
,
получаются расчетные формулы метода
хорд и метода касательных.
Оценка приближения.
Из условия (4)
,
учитывая, что
,
получаем
.
(1)
Приведем без доказательства еще одну формулу для оценки погрешностей.
.
(2)
Из (1) и (2) следует, что итерационный
процесс сходится тем быстрее, чем меньше
.
Если
,
погрешность удобно оценить так:
последовательные приближения
и
,
в этом случае лежат по разные стороны
от корня
.
Поэтому
.
(3)
Если за приближенное значение корня
взять полусумму последних полученных
приближений
,
то
.
Пример: Вычислить приближенно действительный корень уравнения.
.
при всех
.
Сузим этот интервал методом половинного
деления.
Вычислим
,
поэтому
.
!
поэтому заменяем исходное уравнение
равносильным
,
получаем
;
.
Находим
,
такое чтобы
при
.
Пусть
Тогда
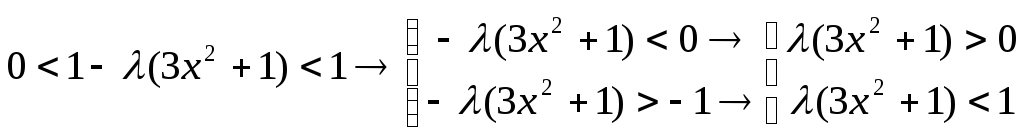
При
,
Получаем
.
Пусть
При таком
выполняется достаточное условие
сходимости итерационного процесса,
т.к.
;
.
Выбираем
Подставляем
,
в правую часть уравнения
получаем
Аналогично находим:
;
;
;
;
;
;
;
;
Оценим погрешность по формуле
Итак
;
1) Условие сходимости
всегда выполняется для функций
,
где
.
2) Если производная
отрицательна на отрезке
,
то уравнение
,
заменяется на
.
ЛЕКЦИЯ 8