
- •2202 “Автоматизированные системы обработки
- •Приближенные числа.
- •Действия над приближенными числами.
- •Общая схема метода Гаусса для систем, имеющих единственное решение
- •Обратный ход:
- •Метод Гаусса с выбором максимального элемента по столбцу
- •Достаточное условие сходимости процесса итераций
- •Основные понятия алгебры матриц и теории линейных векторных пространств.
- •Обратная матрица
- •Правило нахождения ранга матрицы:
- •Нахождение обратной матрицы методом Гаусса
- •Применение метода итераций для умножения элементов обратной матрицы
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений
- •Пример:
- •Блок – схема решения уравнения f(X) методом половинного деления
- •Метод хорд
- •Метод Ньютона
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций
- •Теорема
- •Оценка приближения.
- •Интерполирование функций.
- •1. Конечные разности различных порядков.
- •2) Таблица разностей.
- •3) Постановка задачи интерполирования.
- •4) Первая интерполяционная формула Ньютона.
- •Блок-схема построения кубического сплайна
- •Численное дифференцирование
- •2.Конечно-разностные аппроксимации производных.
- •Блок-схема вычисления производной.
- •Численное интегрирование.
- •Блок-схема вычисления определенного интеграла методом двойного пересчета по формуле Симпсона.
- •Квадратурные формулы Гаусса
- •Приближенное вычисление несобственных интегралов с бесконечными пределами.
- •Среднеквадратичное приближение функций
- •Точечное квадратичное аппроксимирование функций
- •Условия нахождения экстремума функции
- •IV Интегральное квадратичное аппроксимирование функций на отрезке.
- •Ортогональные на промежутке системы функций
- •Основные понятия гармонического анализа.
- •4.2.1. Аппроксимация тригонометрическими полиномами кусочно-гладких функций
- •4.3. Среднеквадратичное приближение функций полиномами Лежандра.
- •4.3. Полиномы, наименее уклоняющиеся от нуля.
- •Эмпирические формулы
- •Численное решение обыкновенных дифференциальных уравнений.
- •Численное решение дифференциальных уравнений и систем дифференциальных уравнений высших порядков
- •Численные методы безусловной оптимизации.
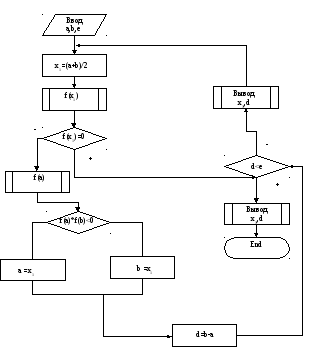
Блок – схема решения уравнения f(X) методом половинного деления
-
Метод хорд
Д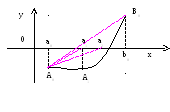 ано
уравнение f(x)=0.
Пусть найден отрезок
ано
уравнение f(x)=0.
Пусть найден отрезок
![]() ,
такой, что на его концах функция f(x)
имеет разные знаки, то есть
,
такой, что на его концах функция f(x)
имеет разные знаки, то есть
![]() .
Пусть, кроме этого, производные
.
Пусть, кроме этого, производные
![]() и
и
![]() на отрезке
на отрезке
![]() сохраняют знак. (Пусть
сохраняют знак. (Пусть
![]() при a0<x<b0).
при a0<x<b0).
За приближенное значение корня принимаем точку пересечения с осью ОХ хорды, проходящей через точки A0[a0,f(a0)], B0[b0,f(b0)]
Уравнение хорды:
![]() (1)
(1)
Точка пересечения a1 с осью ОХ находится из (1) при у=0 (при этом х=а1):
![]() (2)
(2)
Принимая а1 за конец первого
отрезка
![]() ,
можно снова провести хорду и получится
приближенное значение а2
,
можно снова провести хорду и получится
приближенное значение а2
![]() (3)
(3)
И так далее
![]() (4)
(4)
Можно показать, что процесс сходится и
в пределе
![]() .
.
-
Метод Ньютона
Пусть ξ – корень уравнения f(x)=0
определен на отрезке![]() причем
причем
![]() и
и
![]() непрерывны и сохраняют знаки при a<x<b.
Найдя какое-нибудь n-ое
приближенное значение корня xn=
ξ (a≤xn≤b),
мы можем уточнить его по методу Ньютона.
непрерывны и сохраняют знаки при a<x<b.
Найдя какое-нибудь n-ое
приближенное значение корня xn=
ξ (a≤xn≤b),
мы можем уточнить его по методу Ньютона.
Положим
![]() (1)
(1)
Где hn-малая величина.
По формуле Тейлора, беря только линейные члены находим:
![]() (2)
(2)
Так как
![]() - «корень», то
- «корень», то
![]()
Из (2) следует:
![]()
Подставляя hn в (1), получаем новое приближение корня:
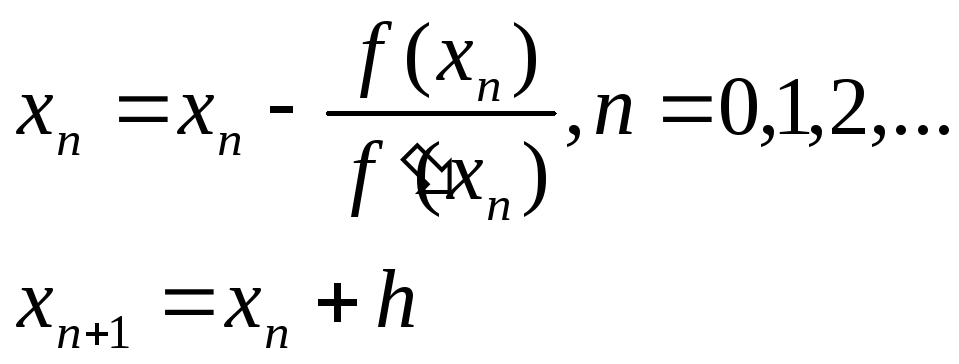
 (3)
(3)
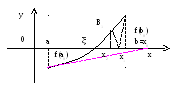
Так как уравнение касательной в точке Bn[bn,f(bn)]:
![]()
Полагая у=0 (корень!); xn=xn+1 получим
![]()
Поэтому метод Ньютона называют еще методом касательных.
Если в качестве начального приближения
выбрать точку а, то получили бы новое
приближение, выходящее за интервал
![]() .
Следовательно «хорошим» начальным
приближением x0
является то, для которого выполнено
неравенство:
.
Следовательно «хорошим» начальным
приближением x0
является то, для которого выполнено
неравенство:
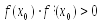 (4)
(4)
Для оценки точности (погрешности) n-го приближения xn можно воспользоваться следующим соотношением:
![]() ,
,
Т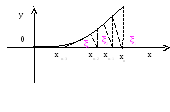 о
есть «установившееся» начальные
десятичные знаки приближения xn
и xn+1,являются
верными (следует взять более двух
последующих приближений!)
о
есть «установившееся» начальные
десятичные знаки приближения xn
и xn+1,являются
верными (следует взять более двух
последующих приближений!)
Пример:
Вычислить методом Ньютона отрицательный корень уравнения:
![]()
с пятью верными знаками.
Решение:
Полагая х=0,-10,-100,…, получим f(0)=-10000, f(-10)=-1050, f(-100)≈108
Искомый корень находится в интервале [-100,-10]. Сузим интервал, рассматривая точку х=-11 f(-11)=3453.
Таким образом -11<ξ<-10
На этом интервале
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то есть
,
то есть
![]() ,
за начальное приближение выбираем
х0=-11.
,
за начальное приближение выбираем
х0=-11.
Результаты вычислений сводим в таблицу:
|
n |
xn |
f(xn) |
|
|
|
0 |
-11 |
3453 |
-5183 |
0.7 |
|
1 |
-10.3 |
134.3 |
-4234 |
0.03 |
|
2 |
-10.27 |
37.8 |
-4196 |
0.009 |
|
3 |
-10.261 |
0.2 |
- |
- |
Останавливаемся на n=3.
проверяем точность решения, давая
приращение
![]() .
(два знака до запятой, три знака – после)
.
(два знака до запятой, три знака – после)
-5 значащих цифр.
![]()
-10261<ξ<-10260
Любое из этих чисел дает искомое приближение. (А хорошо бы еще 1-2 итерации выполнить)
ЛЕКЦИЯ 7
Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций
(метод последовательных приближений)
Пусть дано уравнение:
f(x)=0 (1)
где f(x)
– непрерывная функция. требуется
вычислить действительный корень
уравнения (1) находящийся на отрезке
![]() .
.
Заменим уравнение (1) на равносильным ему уравнением
![]() (2)
(2)
где
![]() - непрерывна на
- непрерывна на
![]() функция.
функция.
Выбираем произвольное
![]() и подставляем его в правую часть равенства
(2). Получаем
и подставляем его в правую часть равенства
(2). Получаем
![]()
Аналогично получаем
![]()
![]()
![]()
Рассмотрим последовательность x0,x1,x2,…,xn,…
Пусть эта последовательность сходится,
то есть существует предел
![]() .
Покажем, что с – корень уравнения (2) По
построению
.
Покажем, что с – корень уравнения (2) По
построению
![]() причем
причем
![]() -
непрерывная функция. Переходя к пределу
при
-
непрерывная функция. Переходя к пределу
при
![]() ,
получаем
,
получаем
![]() что и требовалось доказать.
что и требовалось доказать.
Так как уравнения (1) и (2) равносильны, то c-корень и уравнения (1), то есть исходного уравнения.
Выясним при каких значениях процесс сходится.
