
- •2202 “Автоматизированные системы обработки
- •Приближенные числа.
- •Действия над приближенными числами.
- •Общая схема метода Гаусса для систем, имеющих единственное решение
- •Обратный ход:
- •Метод Гаусса с выбором максимального элемента по столбцу
- •Достаточное условие сходимости процесса итераций
- •Основные понятия алгебры матриц и теории линейных векторных пространств.
- •Обратная матрица
- •Правило нахождения ранга матрицы:
- •Нахождение обратной матрицы методом Гаусса
- •Применение метода итераций для умножения элементов обратной матрицы
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений
- •Пример:
- •Блок – схема решения уравнения f(X) методом половинного деления
- •Метод хорд
- •Метод Ньютона
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций
- •Теорема
- •Оценка приближения.
- •Интерполирование функций.
- •1. Конечные разности различных порядков.
- •2) Таблица разностей.
- •3) Постановка задачи интерполирования.
- •4) Первая интерполяционная формула Ньютона.
- •Блок-схема построения кубического сплайна
- •Численное дифференцирование
- •2.Конечно-разностные аппроксимации производных.
- •Блок-схема вычисления производной.
- •Численное интегрирование.
- •Блок-схема вычисления определенного интеграла методом двойного пересчета по формуле Симпсона.
- •Квадратурные формулы Гаусса
- •Приближенное вычисление несобственных интегралов с бесконечными пределами.
- •Среднеквадратичное приближение функций
- •Точечное квадратичное аппроксимирование функций
- •Условия нахождения экстремума функции
- •IV Интегральное квадратичное аппроксимирование функций на отрезке.
- •Ортогональные на промежутке системы функций
- •Основные понятия гармонического анализа.
- •4.2.1. Аппроксимация тригонометрическими полиномами кусочно-гладких функций
- •4.3. Среднеквадратичное приближение функций полиномами Лежандра.
- •4.3. Полиномы, наименее уклоняющиеся от нуля.
- •Эмпирические формулы
- •Численное решение обыкновенных дифференциальных уравнений.
- •Численное решение дифференциальных уравнений и систем дифференциальных уравнений высших порядков
- •Численные методы безусловной оптимизации.
Приближенное решение алгебраических и трансцендентных уравнений
В трансцендентных уравнениях неизвестные входят под знаком трансцендентных функций, то есть неалгебраических, то есть тригонометрических показателей и др.
Пусть дано уравнение
![]() (1)
(1)
где функция f(x)
определена и непрерывна в некотором
конечном или бесконечном интервале
![]() .
.
Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0, называется корнем уравнения (1) или нулем функции f(x).
Будем предполагать, что уравнение (1) имеет лишь изолированные корни, то есть для каждого корня уравнения (1) существует окрестность , не содержащая других корней этого уравнения.
Приближенное нахождение изолированных действительных корней уравнения (1) складывается обычно из двух этапов:
-
отделение корней, то есть установление возможно тесных промежутков [α, β], в которых содержится один и только один корень уравнения (1);
-
уточнение приближенных корней, то есть доведение их до заданной степени точности.
Для отделения корней используются следующая теорема:
Теорема
Если непрерывная функция f(x)
принимает значение разных знаков на
концах отрезков [a, b],
то есть
![]() ,
то внутри этого отрезка находится по
крайней мере один корень уравнения
f(x)=0.
если производная
,
то внутри этого отрезка находится по
крайней мере один корень уравнения
f(x)=0.
если производная
![]() сохраняет
свой знак на отрезке [a,
b], то корень будет
единственный.
сохраняет
свой знак на отрезке [a,
b], то корень будет
единственный.
Процесс нахождения корней
Определяем знаки функции f(x)
в ряде точек из области определения
функции х1,х2,х3,…,
выбор которых учитывается особенностью
функции f(x).
если окажется, что
![]() ,
то на отрезке [xk,xk+1],
то имеется по крайней мере один корень
уравнения f(x)=0.
Необходимо каким-либо способом проверить,
является ли этот корень единственным.
,
то на отрезке [xk,xk+1],
то имеется по крайней мере один корень
уравнения f(x)=0.
Необходимо каким-либо способом проверить,
является ли этот корень единственным.
Пример:
Определить действительные корни уравнения:
![]()
|
х |
-1 |
0 |
1 |
2 |
3 |
|
f(x) |
- |
- |
- |
- |
+ |
На отрезке [2,3] имеется корень уравнения,
так как
![]() при всех х, то этот корень единственный.
при всех х, то этот корень единственный.
Для отделения корней можно использовать графические методы.
-
Нахождение корней методом половинного деления
Пусть дано уравнение f(x)=0, (1)
П ричем
f(x)
непрерывна на отрезке [a,
b] и
ричем
f(x)
непрерывна на отрезке [a,
b] и
![]() .
Делим отрезок пополам и находим середину
.
Делим отрезок пополам и находим середину
![]()
Если f(x1) ≠0 то для продолжения вычисления выберем ту из частей данного отрезка [a, х1] или [х1, b]. Концы нового отрезка обозначим через a1 и b1 .
![]()
Продолжаем процесс пока не получим либо точный корень уравнения (1) либо не достигнуто значение с заданной точностью. Для оценки точности используется соотношение:
![]() (2)
(2)
Из (2) получаем:
![]() (3)
(3)
![]() с погрешностью ε не
превышающей
с погрешностью ε не
превышающей
![]()
Пример:
Методом половинного деления с точностью ε = 10-2 найти корень уравнения
![]()
-
Определяем корни уравнения при
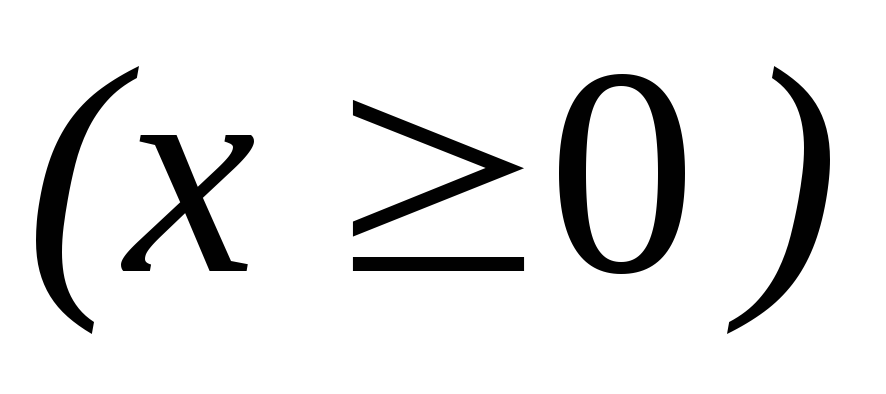
-
x
0
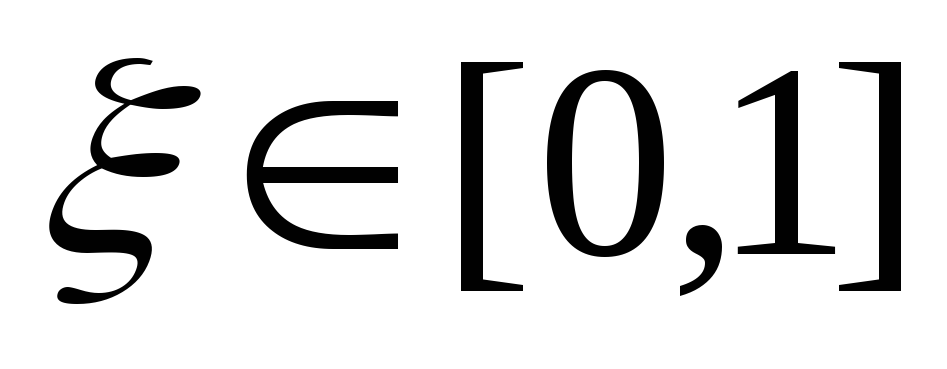 +1
+1f(x)
+
-
-
Уточняем значение корня:
-
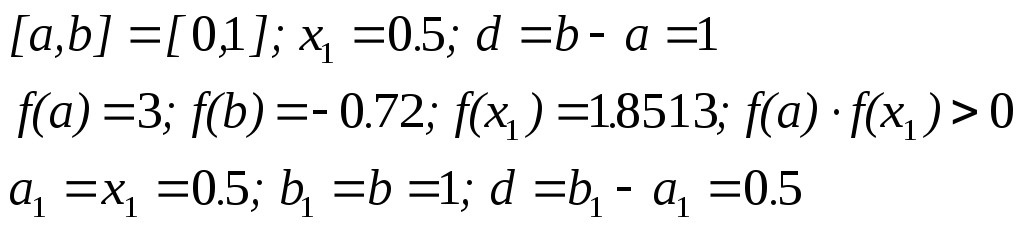
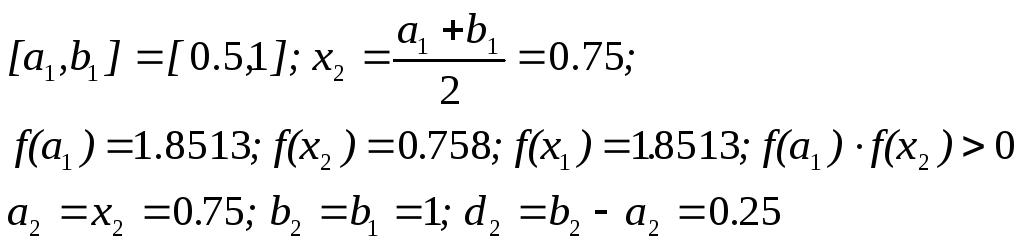
![]()
![]() и
т.д.
и
т.д.
Заданная точность достигается на седьмом шаге.
х7 =0.8828125 с погрешностью d7=0,0078125<ε=0.01
