Правило нахождения ранга матрицы:

1. Начиная с миноров первого порядка (элементов матрицы), переходить к минорам больших порядков.

2. Пусть найден минор D r-го порядка, отличный от нуля, тогда нужно вычислить лишь миноры (r+1)-го порядка, окаймляющие минор D. Если все эти миноры равны нулю, то ранг матрицы равен r. Если же хотя бы один отличен от нуля, то эту операцию нужно применять к нему, увеличить ранг матрицы А на 1.

Пример:

Найти ранг матрицы А (4х5)

В матрице содержатся миноры второго порядка, отличные от нуля, например:

Окаймляющий его минор третьего порядка:

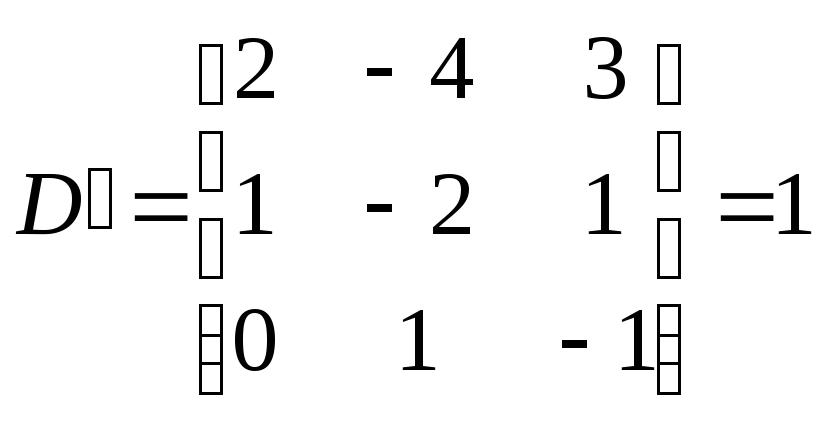
Оба минора четвертого порядка, окаймляющие минор , равны нулю.

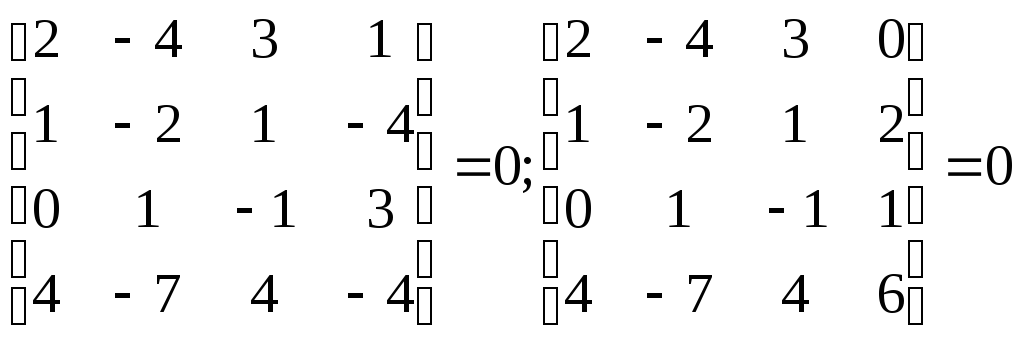
Таким образом, r=3, дефект равен 1: m-r=1.

3. Клеточные матрицы

Разобьем исходную матрицу на блоки или клетки, или подматрицы

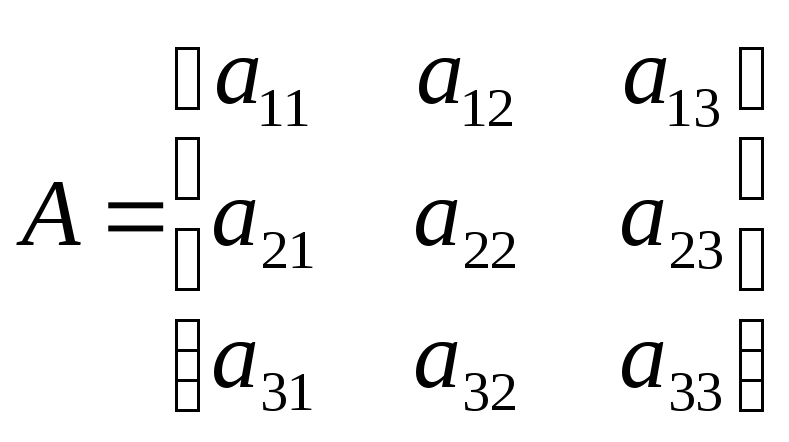
Клетки:

Тогда

Частные случаи клеточных матриц

• Квазидиагональные матрицы

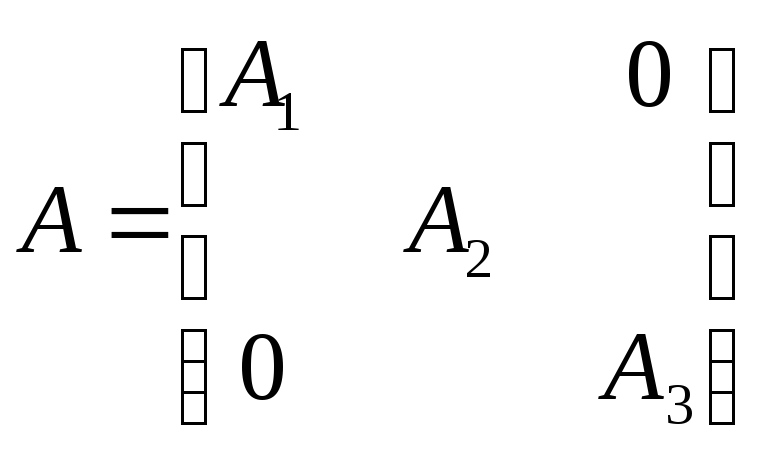
• Окаймленные матрицы

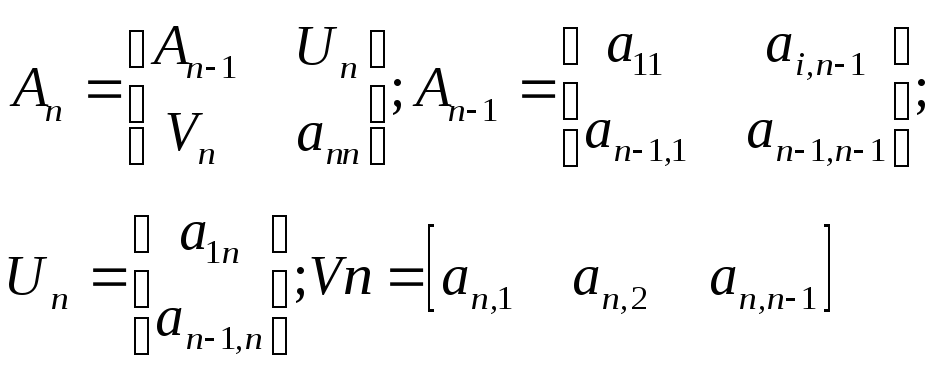
Операции над клеточными матрицами выполняются по аналогии с обыкновенными матрицами (вместо элементов – клетки). При умножении клеточных матриц размеры клеток должны быть согласованны.

Обращение матрицы при разбиении на клетки

Разобьем матрицу А на четыре клетки

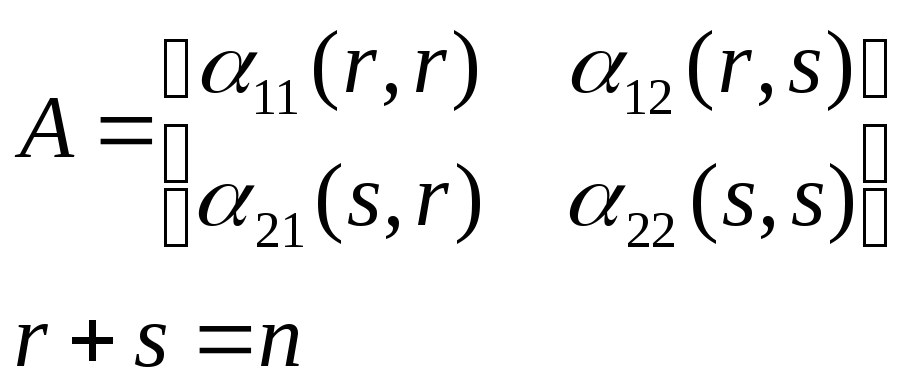
Будем искать обратную матрицу А^-1также в виде четырехклеточной матрицы:

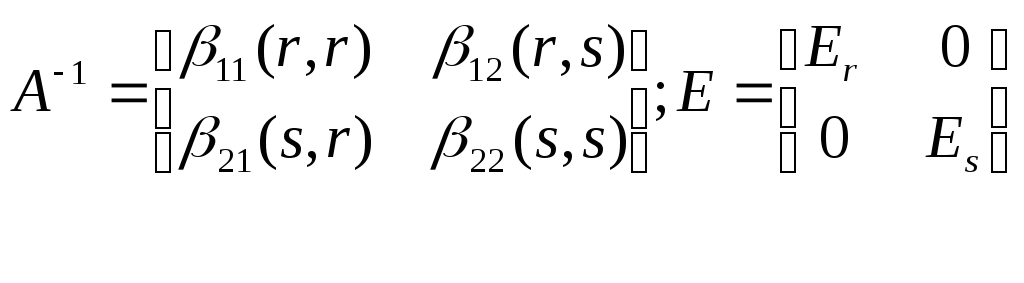
Так как , то перемножая эти матрицы, получим четыре уравнения:

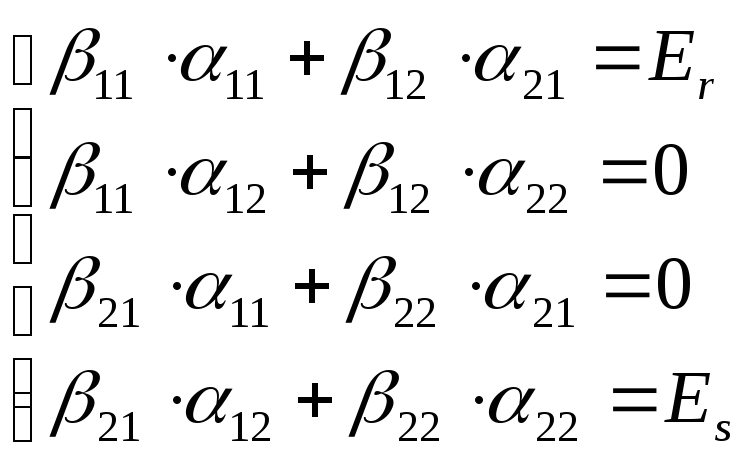(1)

E_s, E_r - единичные матрицы (rxr) (sxs)

Решая уравнения (1), получим:

Вначале находим β₁₂ и β₂₂, а затем β₁₁ и β₂₁

В этом случае приходится обращать матрицы меньшей размерности:

что дает существенный выигрыш в памяти ЭВМ.

4. Нахождение обратной матрицы методом Гаусса

Пусть дана неособенная матрица А и обратная – А^-1

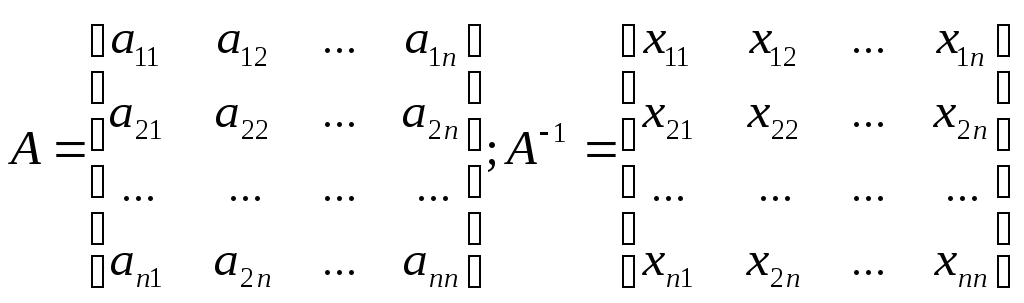
Для вычисления элементов обратной матрицы xij используем соотношение

Умножая матрицы А и А^-1 и сравнивая каждый элемент произведения соответствующему элементу матрицы Е, получим систему уравнений с n² неизвестными x_ij(i,j (1,…n))

Умноженная почленно все строки матрицы А на первый столбец матрицы А^-1 получим первые n уравнений:

(1)

Умножая почленно все строки матрицы А на второй столбец матрицы А^-1 получим вторые n уравнений:

(2)

И так далее.

В общем виде система n² уравнений может быть записана как

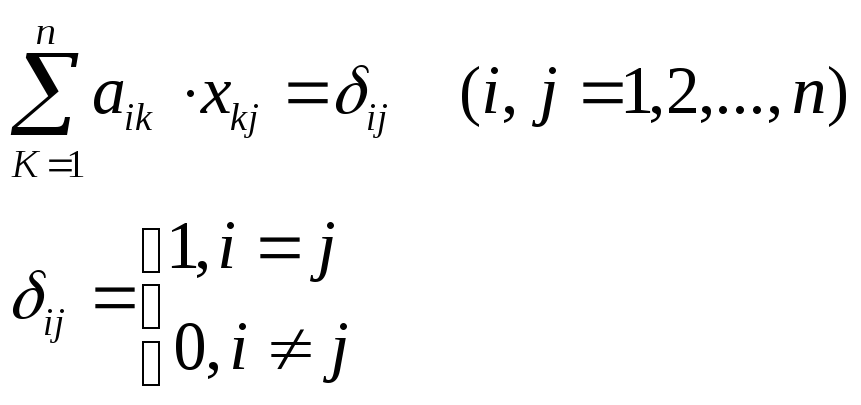
Все n уравнений (n систем вида (1), (2)) имеют одну и ту же матрицу А и различные свободные члены. Решаем систему методом Гаусса.

5. Применение метода итераций для умножения элементов обратной матрицы

Найдем обратную матрицу методом Гаусса.

из-за погрешностей вычислений.

Будем считать полученную матрицу - первым приближением к обратной матрице. Для уточнения элементов матрицы строим итерационный процесс (Демидович и Марон, и др.)

(1)

(2)

Если , то итерационный процесс сходится.

Процесс (1), (2) продолжают до тех пор, пока элементы матрицы F по модулю не станут меньше заданного числа Е. Тогда полагают (можно рассматривать какую-либо норму матрицы F)

Пример:

Уточнить элементы матрицы А^-1. Итерации продолжать до тех пор, пока элементы матрицы F_k по модулю не станут ≤5*10^-5

Решение:

1. Находим F₀ по формуле (1)

2. Находим D₀F₀

3. Находим

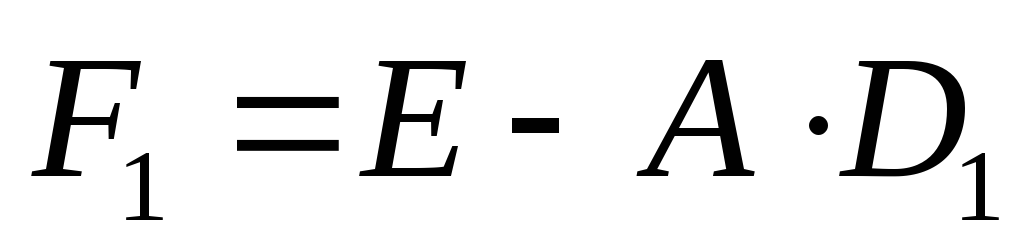
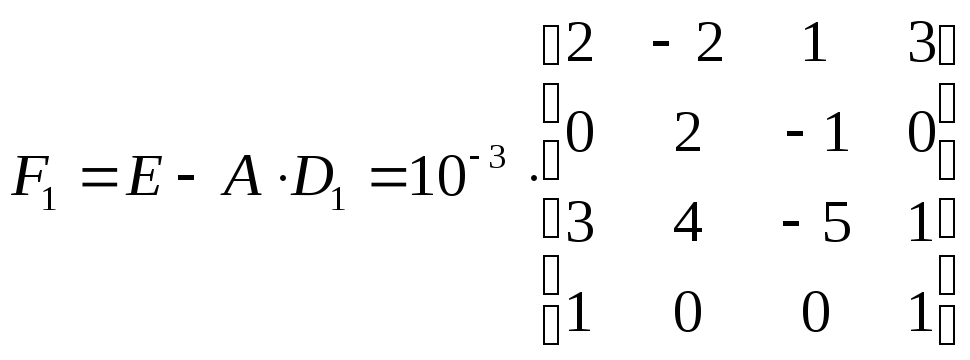
ЛЕКЦИЯ6