Достаточное условие сходимости процесса итераций

Для неприведенной (исходной) системы уравнений (1) достаточное условие сходимости итерационного процесса по m-норме можно представить в виде:

(9)

т.е. если для каждого из уравнений системы (1) модули диагональных элементов больше суммы модулей всех остальных коэффициентов (строки i).

Достаточное условие сходимости процесса для неприведенной системы (1) по l-норме можно представить в виде:

(10)

(модули диагональных элементов больше суммы модулей всех остальных элементов столбца). Если условия (9) не выполняется, следует проверить условие сходимости по l- и k-нормам к системе (1) или после приведения ее к виду (2).

Блок-схема численного решения системы линейных алгебраических уравнений методом итераций

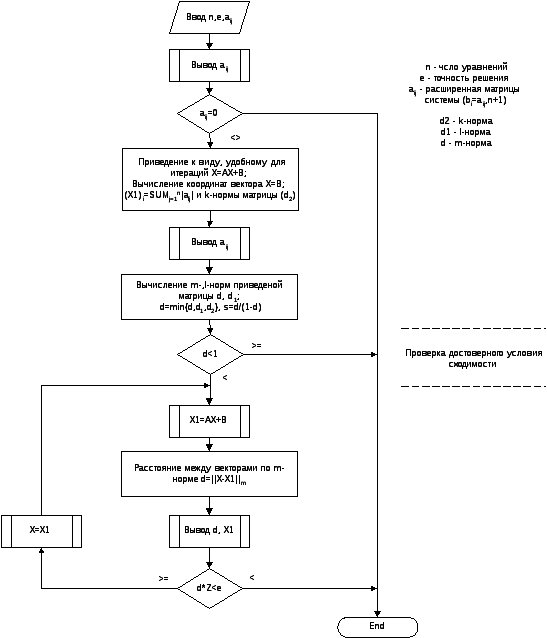
Некоторые более подробные фрагменты блок-схемы численного решения системы уравнений методом итераций

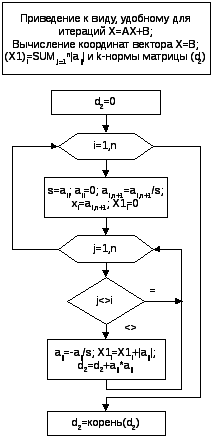
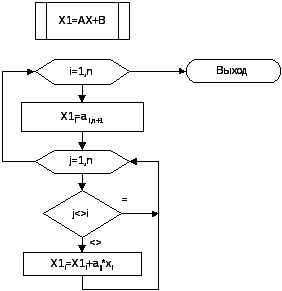
Подпрограмма вычисления вектора на одном шаге итераций (умножение матрицы A на вектор X плюс вектор B)

ЛЕКЦИЯ 5

Основные понятия алгебры матриц и теории линейных векторных пространств.

1. Обратная матрица

Решение системы линейных уравнений

(1)

находится как

(2)

где А^-1-матрица, обратная к А

Обратной матрицей к данной называется матрица, которая, будучи умноженная как справа, так и слева на единичную матрицу, дает единичную матрицу

(3)

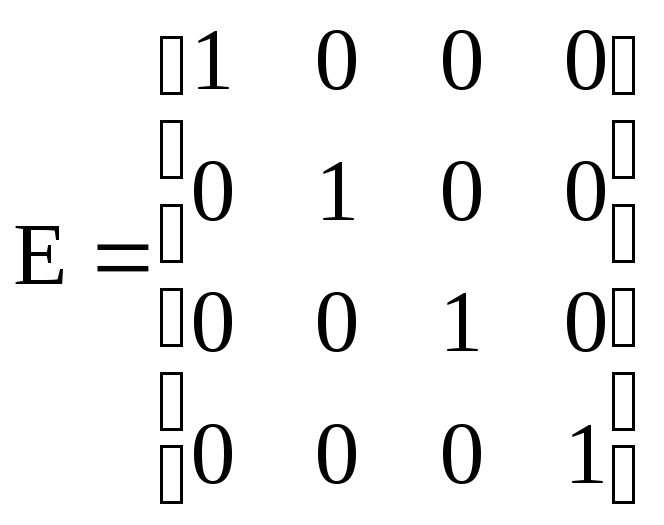
Нахождение обратной матрицы для данной называется обращением данной матрицы. Квадратной матрицей называется неособенной, если ее определитель отличен от нуля. В противном случае – особенная или сингулярная.

Теорема: Всякая неособенная матрица имеет обратную матрицу.

Доказательство:Пусть дана неособенная матрица А

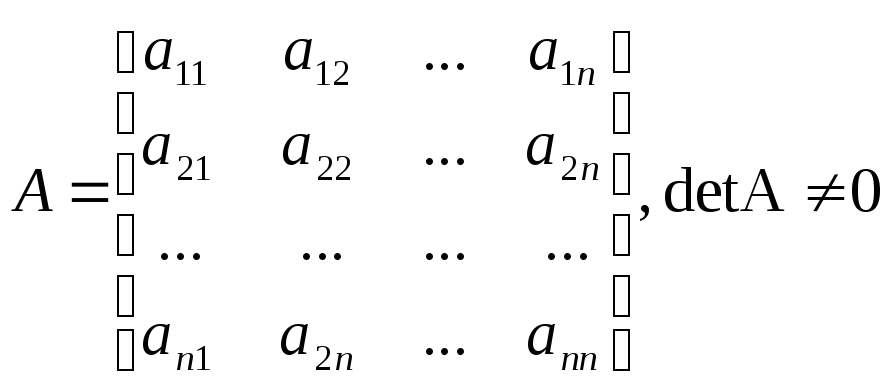
Определитель или детерминант квадратной матрицы А

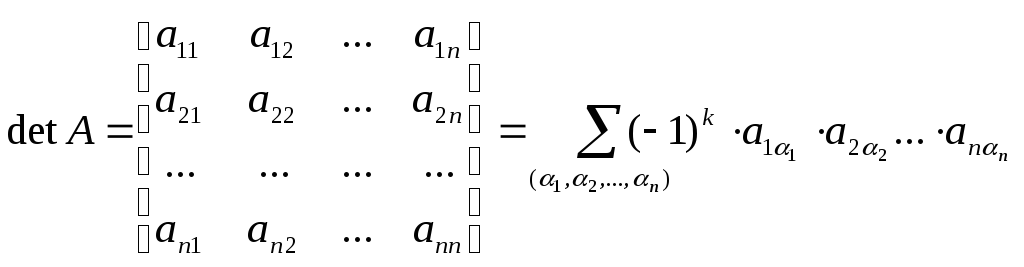(4)

где сумма (4) распространена на всевозможные постановки (α₁,α₂,…α_n) элементов 1,2,3…n и, следовательно, содержит n! Слагаемых, причем n=0, если перестановка четная и n=1, если перестановка нечетная.

Перестановка называется четной, если четно число встречающихся в ней инверсий (Инверсия перестановки: когда α_i<α_j, при i >j)

Составим для матрицы А присоединенную матрицу

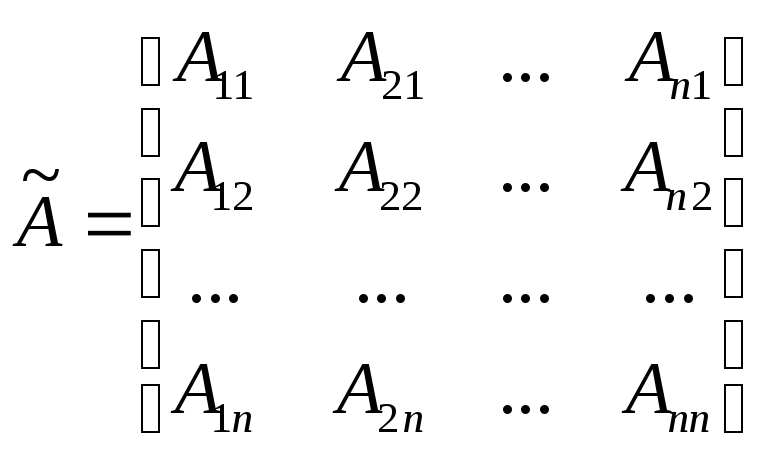
Где А_ij – алгебраическое дополнение (миноры со знаками) соответствующих элементов a_ij(i,j=1,2,3…n)

В присоединенной матрице алгебраические дополнения строк помещаются в соответствующих столбцах, то есть производится операция транспонирования.

Обратная матрица А^*=А^-1 равна , где Δ – определитель

Для данной матрицы А ее обратная матрица А^-1 (если она существует) – единственная.

Теорема:

Особенная обратная матрица обратной не имеет.

Доказательство:

Если А-особенная матрица, то det A=0,

Отсюда следует, что

0=1

Теорема доказана.

Пример:

Для матрицы А найти обратную

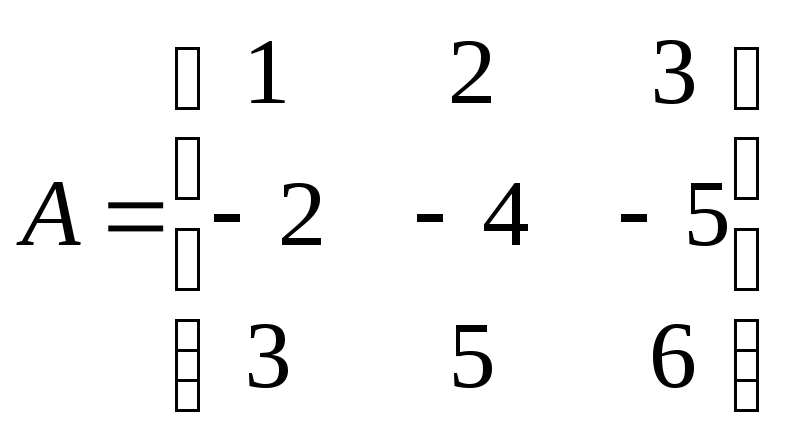
Решение:

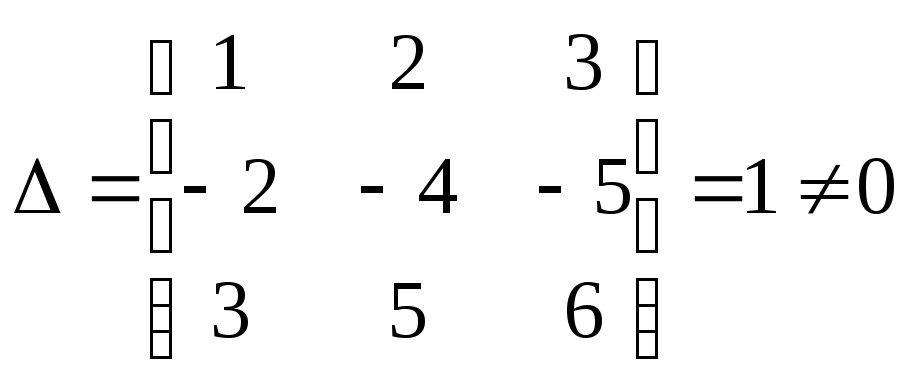
Составляем присоединенную матрицу:

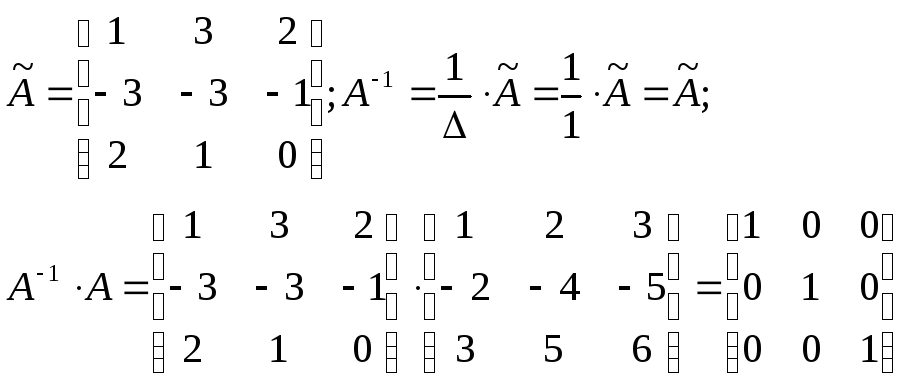
Свойства обратной матрицы:

1. Определитель обратной матрицы равен обратной величине определителя исходной матрицы

2. Обратная матрица произведения квадратных матриц равна произведению обратных матриц сомножителей, взятому в обратном порядке.

3. Транспонированная обратная матрица равна обратной ей транспонированной данной матрицы

2. Ранг матрицы

Определение:

Рангом матрицы называется максимальный порядок минора матрица, отличный от нуля.

Матрица А имеет ранг r, если:

1. Найдется, по меньшей мере, один ее минор второго порядка, отличный от нуля.

2. Все миноры матрицы А порядка 2+1 и выше равны нулю.

Разность между наименьшим из чисел m и n (матрица А имеет размерность mxn) и рангом матрицы r называется дефектом матрицы.

Если дефект матрицы равен нулю, то ранг матрицы – наибольший из возможных для данной матрицы.