Общая схема метода Гаусса для систем, имеющих единственное решение

Пусть . (В противном случае в качестве первого уравнения возьмем какое-либо другое). Разделим первое уравнение на .

Получим

, (4)

где ; ,

Умножим разрешающее уравнение (4) на и вычтем полученное уравнение из второго уравнения системы (3). Аналогично преобразуем остальные уравнения. Система примет вид

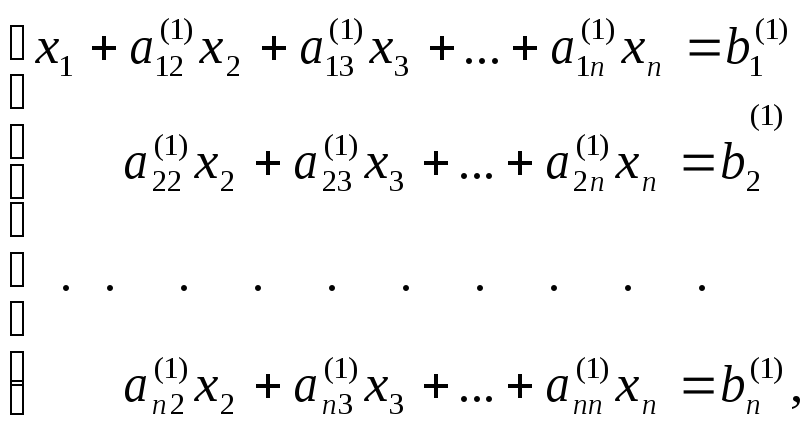(5)

где

Если какой-либо из коэффициентов окажется равным нулю, то j-ое уравнение системы (3) войдет в систему (5) без изменений т.е.

(То есть если в какой-либо из уравнений отсутствовала переменная , то уравнение не преобразуется). Теперь, оставив без изменения первое уравнение системы (5), сделаем разрешающим второе уравнение и применим описанную процедуру к системе из n-1 уравнений, исключая из оставшихся уравнений. Получим систему

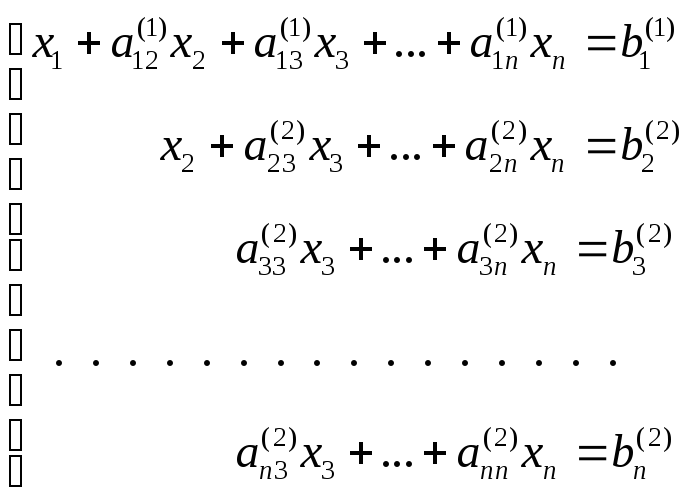
где

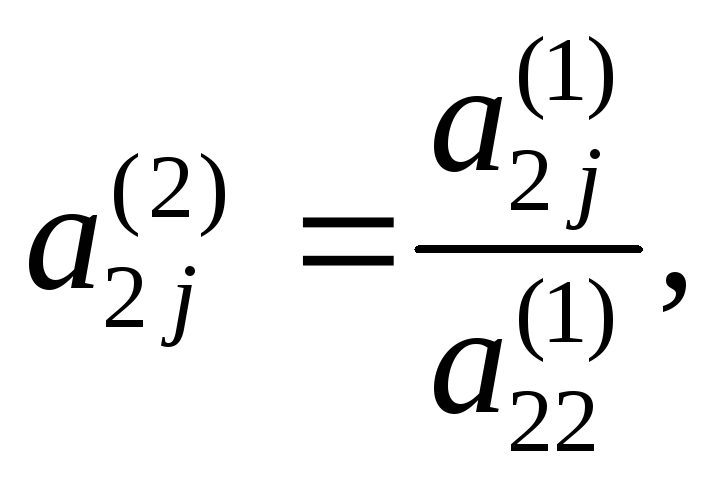
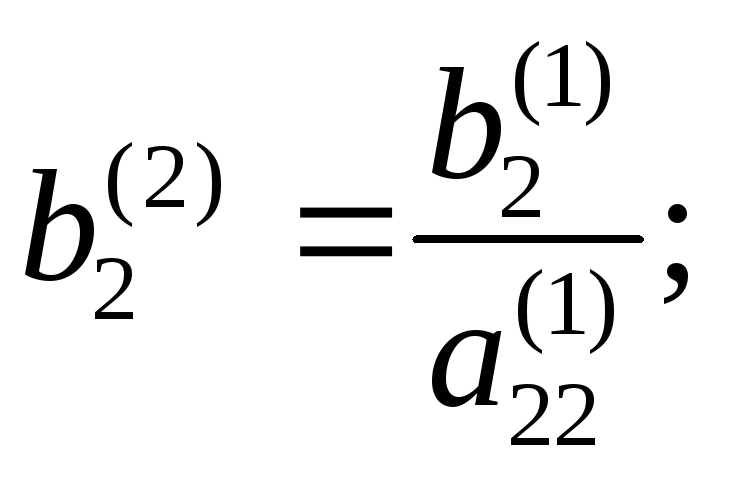
Продолжая аналогичные вычисления, приведем систему (3) к эквивалентной системе с треугольной матрицей коэффициентов

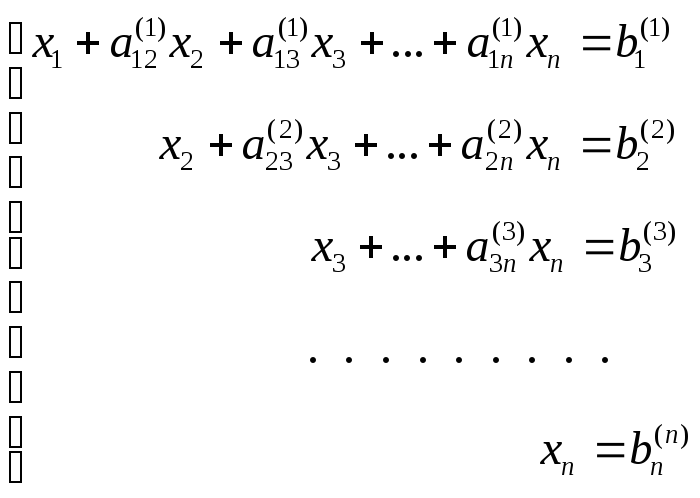(6)

Прямой ход решения выполнен.

Обратный ход:

1. последовательно исключаем неизвестное 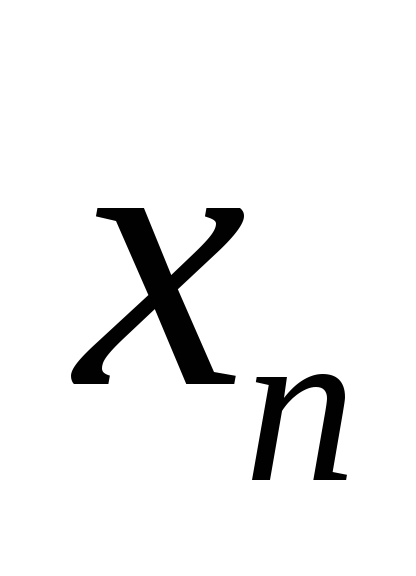, начиная с 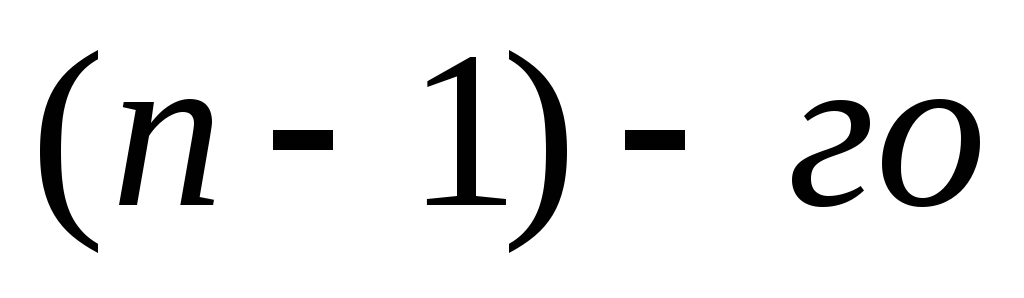уравнения и заканчивая первым. Получаем

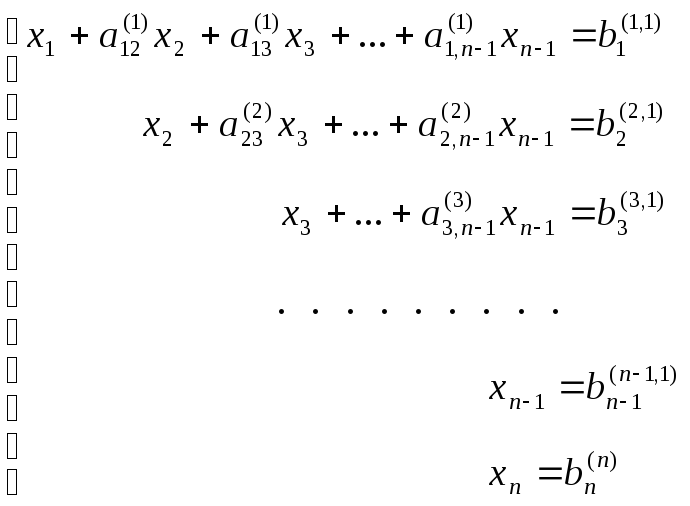(7)

Затем исключаем неизвестное из уравнений с номером j

и т.д.

В результате получаем решение системы

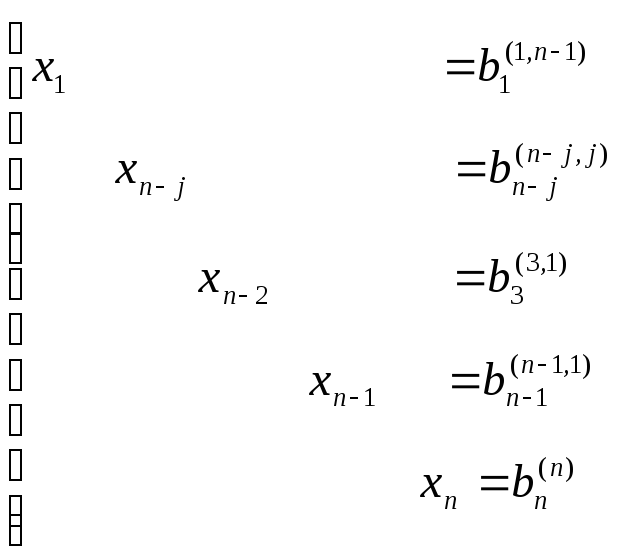
Для уменьшения погрешности вычислений существуют различные модификации метода Гаусса.

Метод Гаусса с выбором максимального элемента по столбцу

В начале первого шага прямого хода среди коэффициентов при неизвестном находят наибольший по модулю. Пусть это . После этого в исходной системе делают перестановку: меняют местами 1-ое и j-ое уравнения. Далее выполняют описанные действия.

В начале второго шага прямого хода максимальный по модулю элемент выбранный среди коэффициентов при неизвестном . Снова возможна перестановка уравнений и исключение из третьего и последующих уравнений и т.д.

При выполнении процедуры прямого хода возможны следующие случаи:

1. матрица А приводится к треугольной (получаю решение).

2. число преобразованных уравнений системы меньше числа неизвестных (ранг матрицы А< n) – Это происходит, если в системе получаются в процессе преобразований тождества 0=0. Система имеет бесконечное множество решений.

3. все коэффициенты при неизвестных в каком-либо уравнении равны нулю, свободный член отличен от нуля. Система не имеет решения.

Блок-схема решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента (по столбцу)

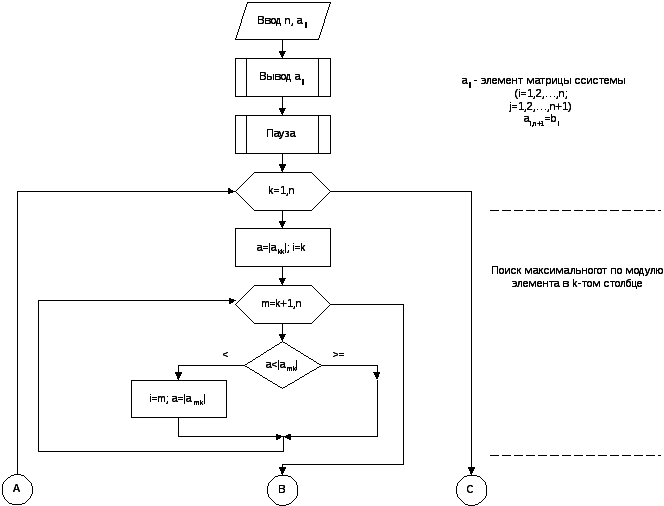
ЛЕКЦИЯ 4

Метод итераций

Рассмотрим систему линейных алгебраических уравнений

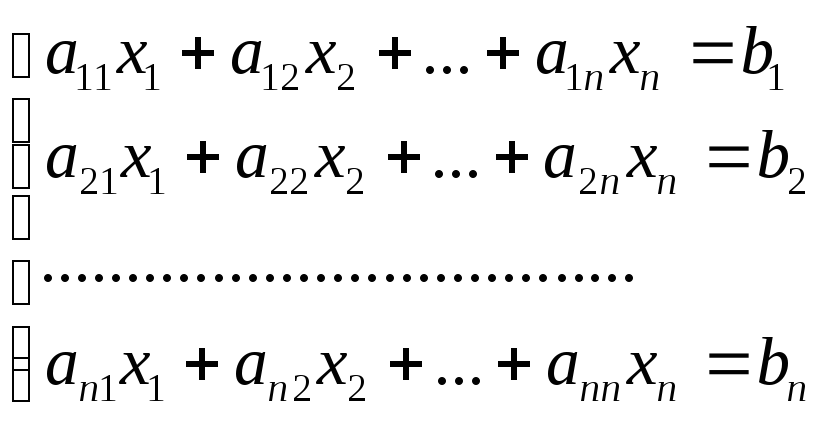(1)

Если все диагональные элементы , то систему (1) можно представить в приведенном виде

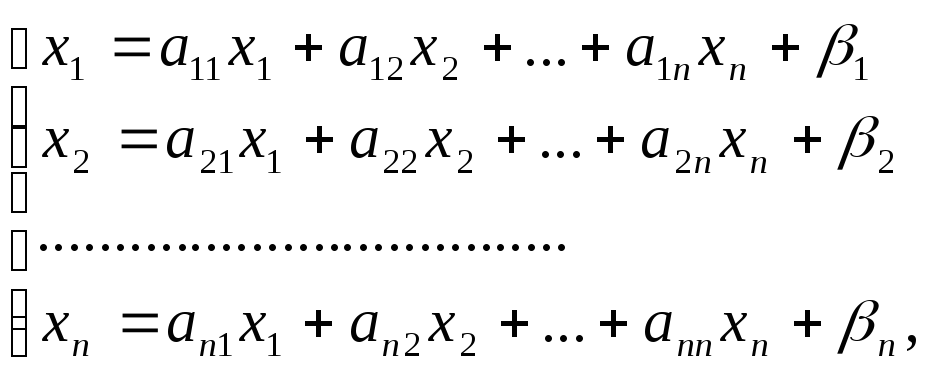(2)

где

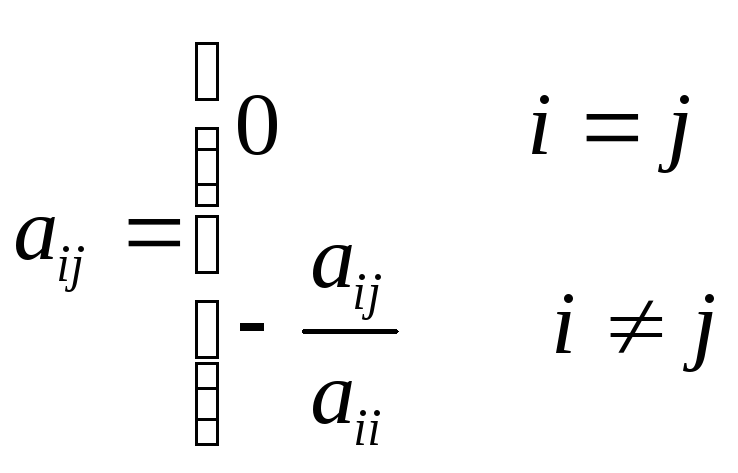
Введем обозначения

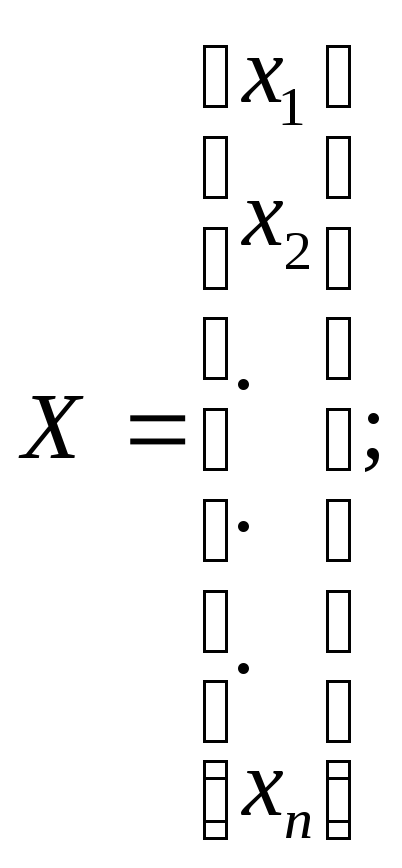
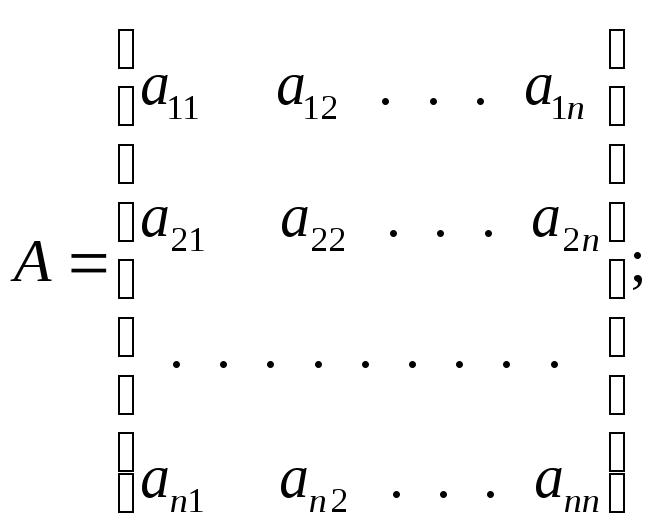
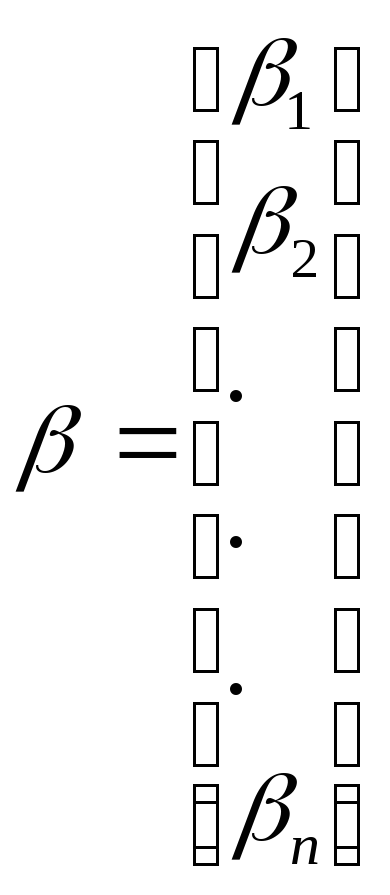
Тогда система (2) запишется в виде

(3)

В качестве начального приближения возьмем вектор  и подставим его в уравнение (3). Получим .Продолжая процесс, получим последовательности приближений:

- первое приближение

-второе приближение (4)

. . . . . . . . .

- (k+1)-ое приближение.

Если существует предел  последовательности векторов то, переходя к пределу в равенстве при , убеждаемся, что  является решением уравнения (3), т.е.

Достаточное условие сходимости итерационного процесса:

Теорема. Если какая-нибудь норма матрицы А меньше единицы: , то уравнение (3) имеет единственное решение , к которому стремится последовательность итераций (4) при любом выборе начального приближения.

Под нормой матрицы понимают следующие выражения:

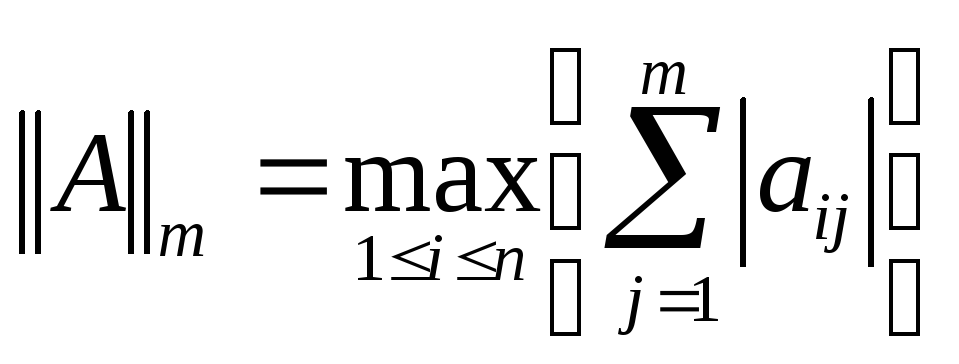(m – норма - максимальное значение суммы модулей элементов строки)

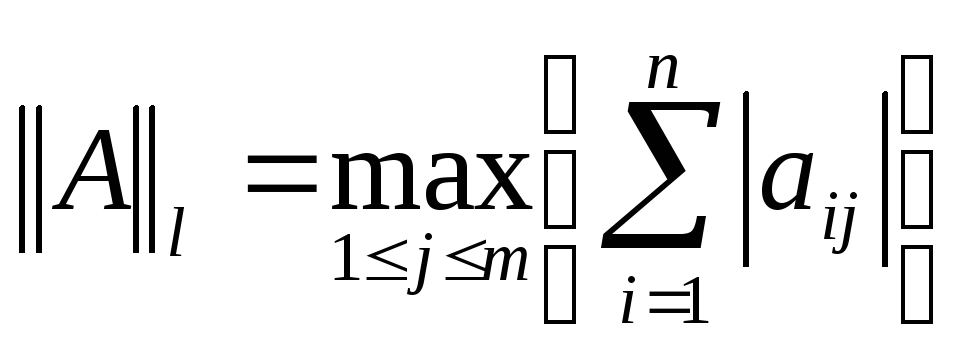(l – норма - максимальное значение суммы модулей элементов столбца)

(k - норма)

Пример: для матрицы

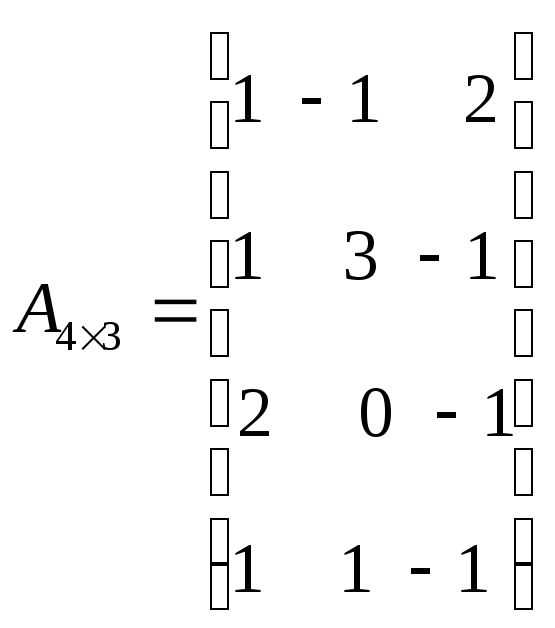
В расчетах полагают . Погрешности приближенного решения уравнения (3) на k-м шаге оценивают неравенством

, (5)

где - норма вектора X

m-норма или кубическая норма

l-норма или октаэдрическая норма

k-норма или сферическая норма.

Из неравенства (5) можно получить оценку числа итераций k, необходимых для обеспечения заданной точности .

Отклонение приближения от решения  по норме не будет превышать , если

(6)

Для вывода (6) достаточно рассмотреть равенства:

; ; ;

;

; и т.д.

Далее .

И, учитывая, что , т.к. норма .

В неравенствах (5) и (6) используются согласованные нормы для матриц и векторов, т.е. m и l-нормы.

Неравенство (6) дает завышенную оценку числа итераций k. Из (6) можно получить удобное условие, позволяющее принять приближение в качестве решения с точностью .

(7)

Пример: Найти решение системы уравнений

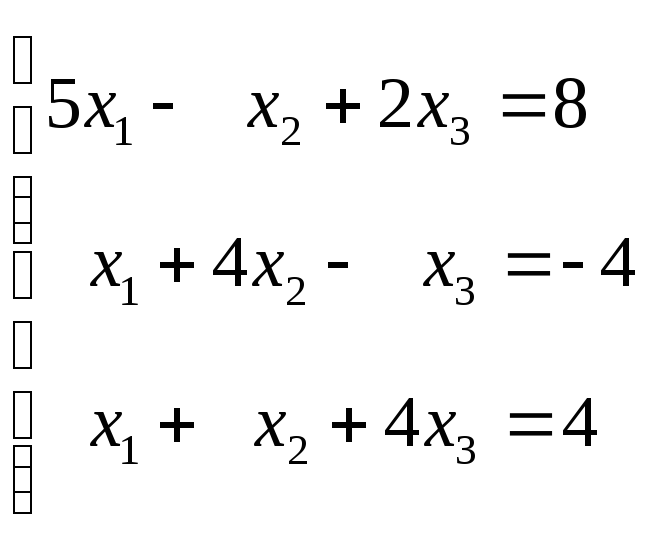
методом итераций с точностью 10^-2.

Решение: Приведем систему к виду (2)

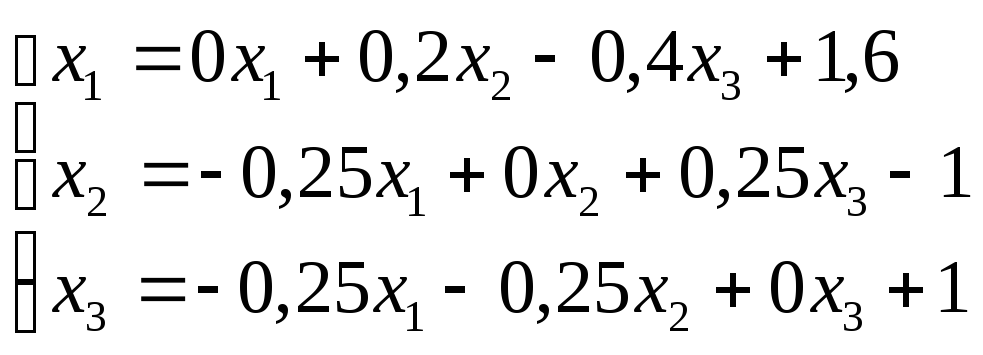
Запишем последовательность итераций

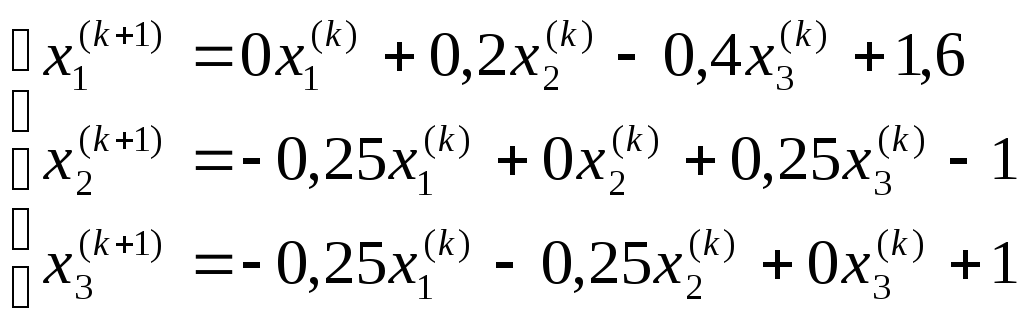(8)

Для приведенной матрицы достаточное условие сходимости выполняется по m-норме:

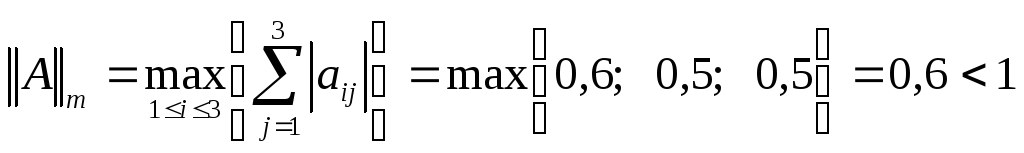
В качестве начального приближения возьмем вектор-столбец свободных членов приведенной системы .

Число итераций для достижения заданной точности определяем из неравенства (6) , которое запишем так:

, действительно: .

; т.к. то ; .

Вычислим теперь три последовательных приближения по формулам (8) и оценим погрешность каждого результата, используя неравенство (6) в виде:

.

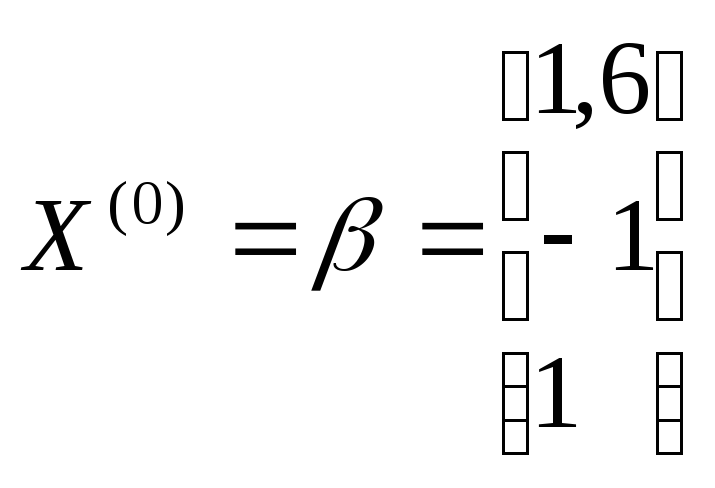
Первое приближение:

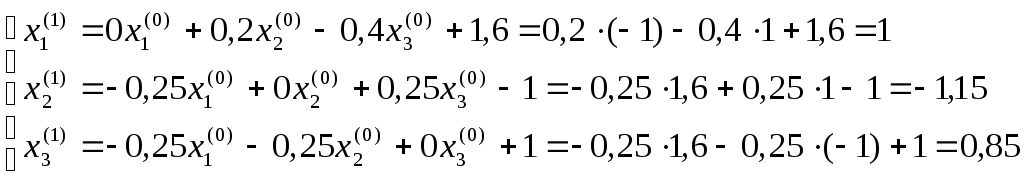
Следовательно, дает значение корня ξ с погрешностью, не превышающей величины .

Далее последовательно находим:

;

.

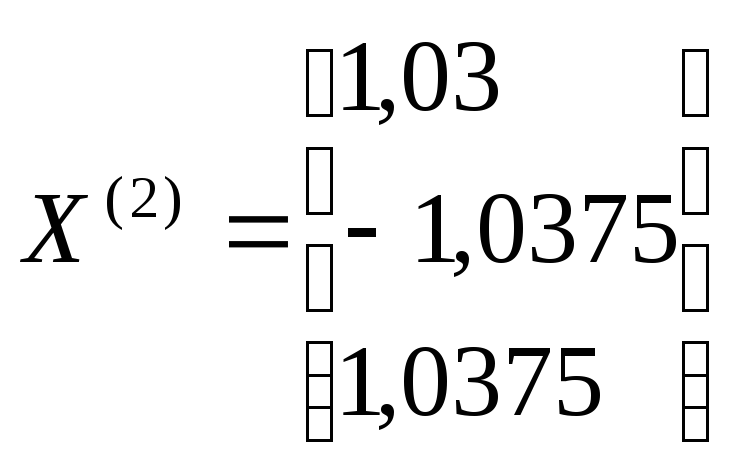Третья итерация:

;

.

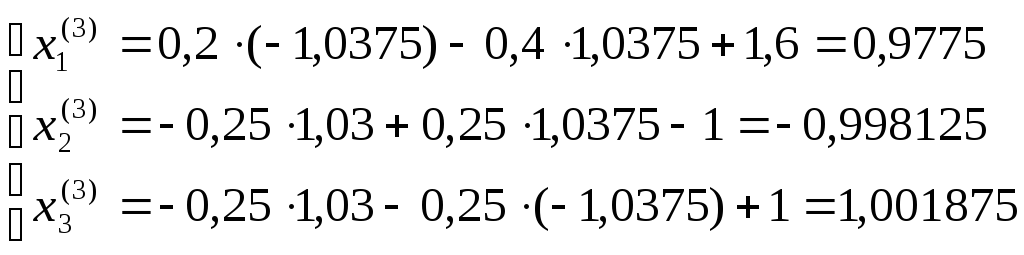
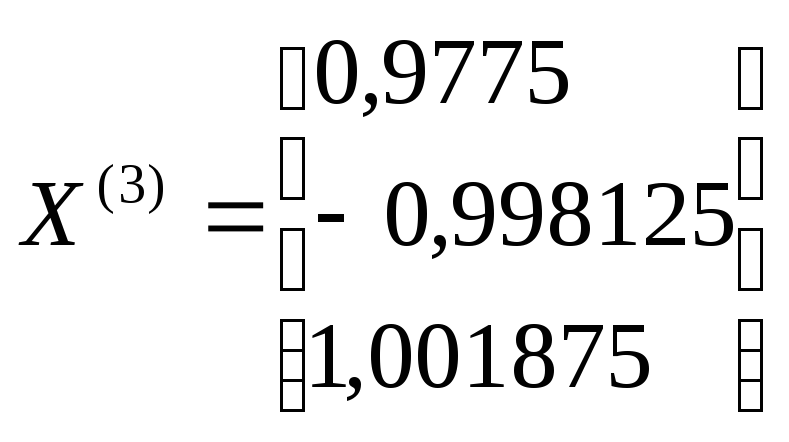Заданная точность достигается за 5 шагов. Точное решение .
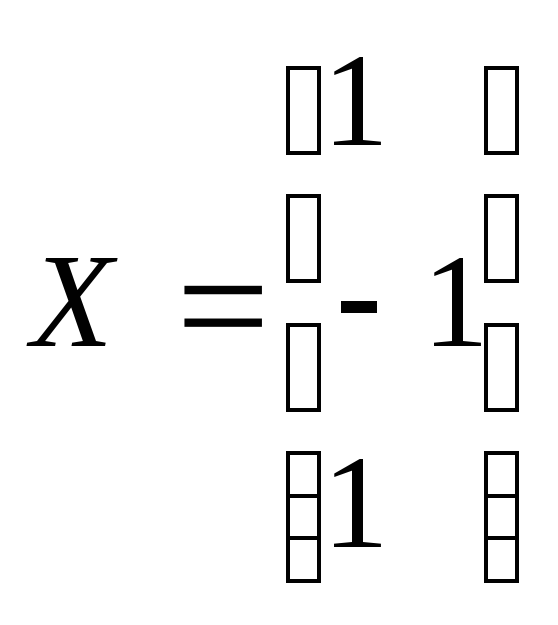