Численное решение дифференциальных уравнений и систем дифференциальных уравнений высших порядков
Задача Коши:
Найти решение уравнения
(1)
При начальных условиях
(2)
Задача Коши (1)-(2) сводится к задаче Коши для системы n DУ-ий 1-го порядка, к которой затем применяют численные методы решения систем.
Положим.
Выразим функцию
вместе с ее производными до (n-1)-го
порядка включительно через выделенные
функции:
Теперь вместо задачи (1)-(2) имеем задачу для системы
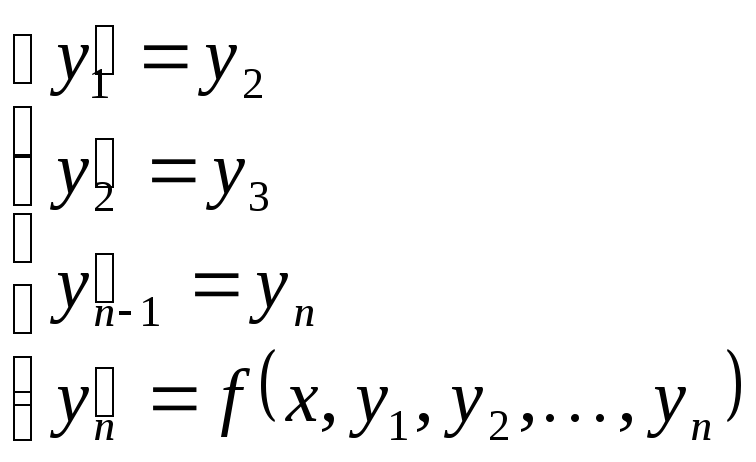(3)
При начальных условиях
(4)
Пример:
Задачу Коши для DУ 2-го порядка преобразовать к задаче Коши для системы двух DУ 1-го порядка.
Решение.
Положим
.
Тогда
Имеем систему:
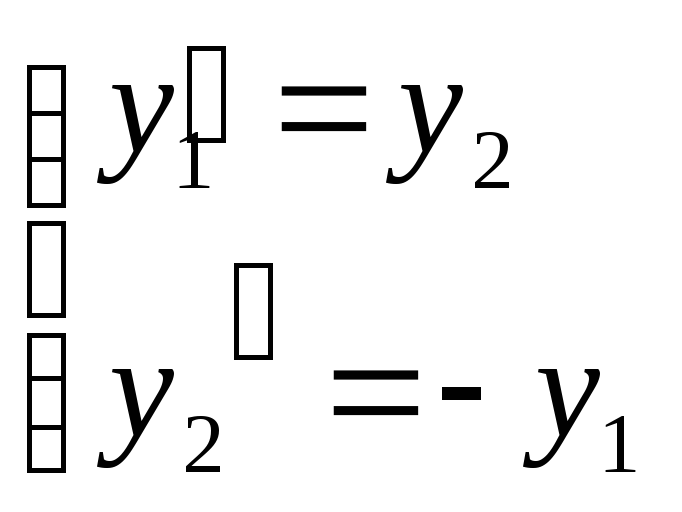
Действительно, из исходного уравнения
имеем систему
Блок-схема численного решения задачи Коши
Для системы DУ первого порядка
Методом Рунге-Кутта.
Рассматривается задача Коши для системы
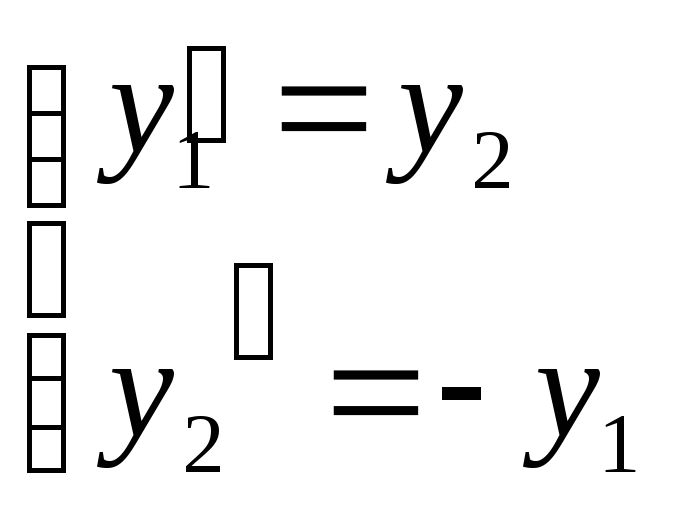
Вычисление правых частей DУ
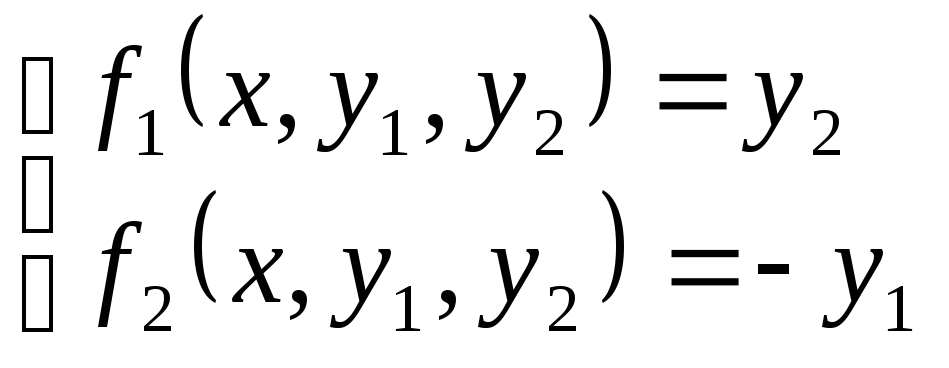
ведутся в подпрограммах. На экран
выводятся приближенные решения на
отрезке
в виде таблицы
значений 2-х функций на равномерной
сетке с шагом
.
Численные методы безусловной оптимизации.
I. Необходимые и достаточные условия экстремума в задачах безусловной оптимизации.
Пусть будет задано множество
и функция
определенная на этом множестве.
(
- линейное, n – мерное
пространство)
Точка
называется точкой локального минимума
функции
на множестве х, если существует шар
такой, что для любого
выполняется неравенство:
(1)
Если неравенство выполняется как строгое
(при
),
то говорят, что
- точка строгого локального минимума.
Точка
называется
точкой глобального минимума функции
на множестве х, если неравенство (1)
выполняется для любого
.
Аналогично определяются точки локального
и глобального максимума
на множестве х.
Точки локального минимума и максимума
функции
называют точками экстремума этой
функции.
Задача отыскания всех локальных минимумов
(max) функции
,
если множество х совпадает со всем
n-мерным пространством,
т.е.
,
называют задачей безусловной
оптимизации, а функция
- целевой функцией.
Задачи оптимизации:
(2)
(3)
Задача (3) эквивалентна задаче
Теорема 1.
Пусть х* - точка локального минимума
функции
,
которая имеет в этой точке непрерывные
частые производные
,
тогда частные производные функции
в этой точке равны нулю, т.е.
Иначе говоря, в точке экстремума градиент функции
Равен нулевому вектору,
т.е.
Точка ч*, удовлетворяющая условию
,
называется стационарной точкой
функции
.
Квадратная матрица А называется
симметричной, если
.
симметричная матрица А называется
неотрицательно определенна, если
для любого
скалярное произведение векторов
и ч неопределенно; т.е.
;
положительно определенной, если
;
неопложительно определенной, если
;
отрицательно определенной, если
.
Теорема 2. (критерий Сильвестра).
Симметричная матрица Ф неотрицательно (положительно) определена тогда и только тогда, когда все главные (угловые) миноры неотрицательны (положительны):
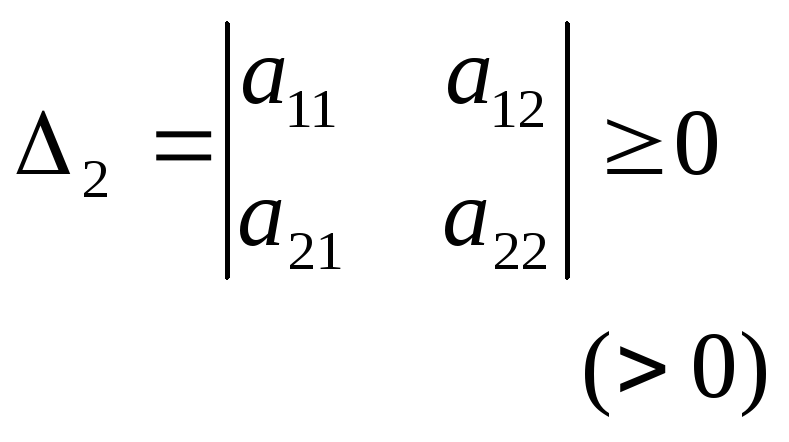и т.д.,
Симметричная матрица А является
неположительно (отрицательно) определенной
тогда и только тогда, когда знаки
последовательных гдавных миноров
чередуются, причем
;
и т.д.
Матрица вторых производных функции
.
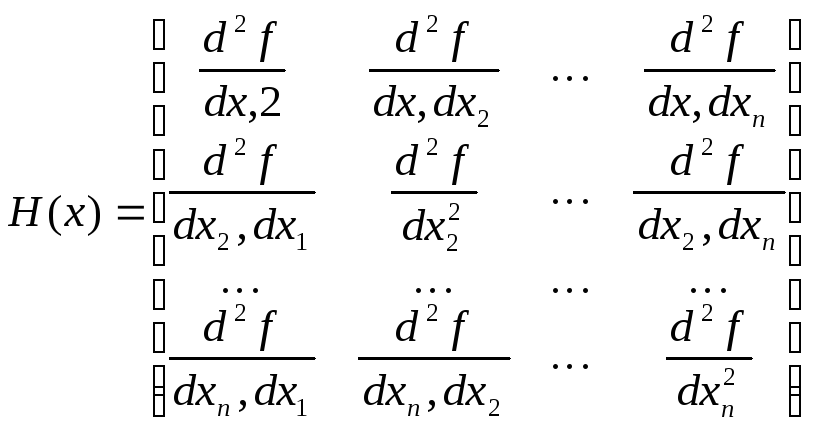
Называется матрицей Гессе функции
.
Теорема 3.
Если точка х* - локальное решение задачи
минимизации, и в этой точке
имеет непрерывные частные производные
до второго порядка включительно, то
матрица Гесса функции
в точке х* является неорицательно
определенной, т.е.
.
Теорема 4. (о достоверных условиях локального экстремума).
Если точка х* является стационарной
точкой функции
,
т.е.
и матрица Гессе функции
в точке х* положительно определена, то
х* - строгое локальное решение задачи
(2)- минимизации.
Если точка х* является стационарной и
матрица Гессе в ней отрицательно
определена, то х* - строгое локальное
решение задачи максимизации функции
.
Для одномерной оптимизации
- условие стационарности
.
- условие минимума
.
(максимума)
.
Пример. Решить задачу.
Решение. Находим стационарные точки
:
Система имеет два решения:
Матрица Гессе:
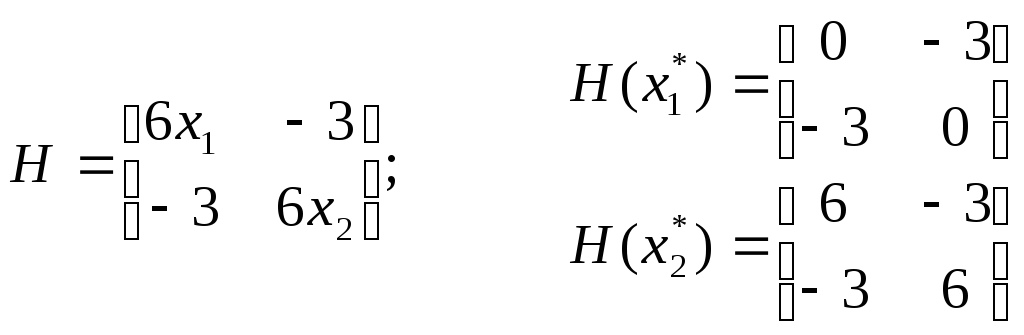
Матрица
не является неотрицательно определенной.
Матрица
- положительно определена.
В.т.
- минимум функции.
II. Выпуклые множества и выпуклые функции
Множество
называется выпуклым, если вместе с
любыми двумя точками
и
ему целиком принадлежит отрезок,
соединяющий эти точки.
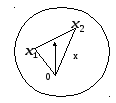
Условия выпуклости:
(4)
Функция
,
определенная на выпуклом множестве
,
называется выпуклой, если
.
Справедливо неравенство
(5)
Если неравенство (S) –
строгое, то функция
строго
выпуклая.
Теорема 5.
Если функция
выпукла на множество Х и Х*.
Является стационарной точкой функции
,
т.е.
,
то х* - строгое локальное решение задачи.
(6)
Теорема 6.
Если функция
и множество х выпуклы, то любое локальное
решение задачи (6) является также
глобальным решением на множество
х.
Теорема 7. (достаточные условия выпуклости функции).
Если
имеет непрерывные производные до 20го
порядка включительно и матрица Гессе
функции
положительно
определена в любой точке х выпуклого
множества х, то
является
выпуклой на множестве х.
Пример.
Показать, что стационарная точка функции
Является глобальным решением задачи
.
Решение.
Находим стационарную точку функции
:
Точка
- решение системы.
Находим матрицу Гессе
.
положительно определена во всех точках
выпуклого множества х (Н не зависит от
х).
Точка х* - решение глобальной задачи минимизации.
Литература
-
Б.П. Демидович, И.А. Марон. «Основы вычислительной математики»
М.: Наука, 1970, 664 с.
2. Н.В.Копченова, И.А. Марон
«Вычислительная математика в примерах и задачах».
М.: Наука, 1972, 367 с.
И.С. Березин, Н.П. Жидков. «Методы вычислений», т 1,т 2. М.: 1962
4. Р.В. Хемминг. «Численные методы для научных работников и инженеров» М.: Мир, , 1977
5. Б.П. Демидович, И.А. Марон, Э.З. Шувалова
«Численные методы анализа». М.: Наука 1967, 368 с.
6. В.И. Ракитин, В.Е. Первушин. «Практическое руководство по методам вычислений». М.: Высшая школа, 1998, 383 с.
7. М.Малькольм, К. Фоулер «Машинные методы математических вычислений». М.: Мир, 1980, 279 с.
8. С.В. Михайленко. «Численные методы (учебное пособие)». Харьков, из-во ХАИ, 1978, 126 с.
9. С.В. Михайленко. «Численные методы (учебное пособие по лабораторному практикуму)». Харьков, из-во ХАИ, 1978, 92 с.
10. Н.С. Бахвалов. «Численные методы». М.: СПб - 2000, 622 с.
11. Н.С. Бахвалов. «Численные методы в задачах и упражнениях». М.: Высшая школа - 2000, 622 с.