Эмпирические формулы
Пусть даны табличные значения
и
.
Необходимо найти аналитическую
зависимость
.
Поиск такой зависимости называют
«сглаживанием» экспериментальных
данных. Сглаживание можно производить,
используя метод наименьших квадратов
(МНК). При этом следует указать вид
эмпирической формулы
(1)
Затем находится сумма квадратов отклонений
(2)
и ищется ее минимум из условий
,
(3)
В общем случае система уравнений (3) нелинейна. Ее можно решить, применяя итерационные методы.
-
Более простым методом является метод выравнивания, при котором нелинейная зависимость (1) может быть сведена к линейной.
Пусть экспериментальные точки
и
не располагаются вблизи прямой. Это
свидетельствует о нелинейной зависимости
между
и
.
Вводятся новые переменные
.
(4)
так, чтобы преобразованные экспериментальные
данные
;
менее уклонялись от прямой. Для
аппроксимирующей прямой
(5)
Коэффициент
и
можно определить из уравнений (2) и (4)
Окончательный результат получают в виде
(6)
Далее уравнение (6) разрешается относительно
.
Пример: Установить вид эмпирической
формулы
используя зависимость (1) с двумя
параметрами
и определить наилучшие значения
параметров, если данные представлены
таблицей
-
1
2
3
4
5
7.1
27.8
62.1
110
161
Решение: Строим график
.
Точки не лежат на прямой.
Делаем преобразование:
;
.
Составим таблицу преобразованных данных
-
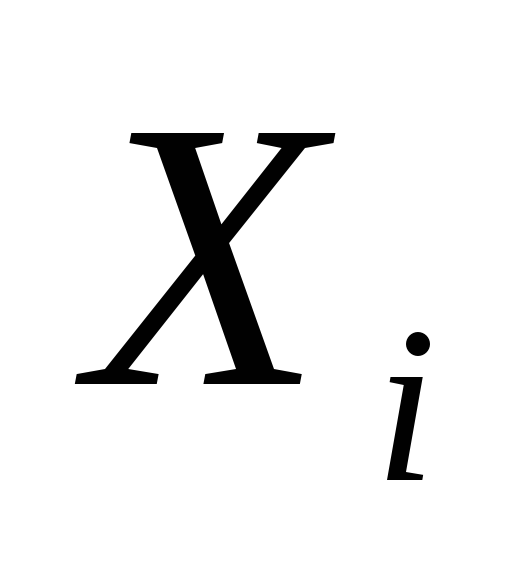
0.000
0.693
1.099
1.386
1.609
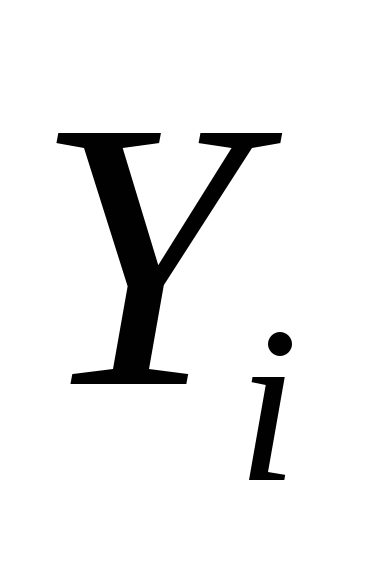
1.960
3.325
4.128
4.700
5.081
Строим график и убеждаемся, что связь
между
и
почти линейная.
Составляем уравнение
Находим
и
,
и приравниваем их нулю.
Получаем систему двух уравнений с двумя неизвестными:
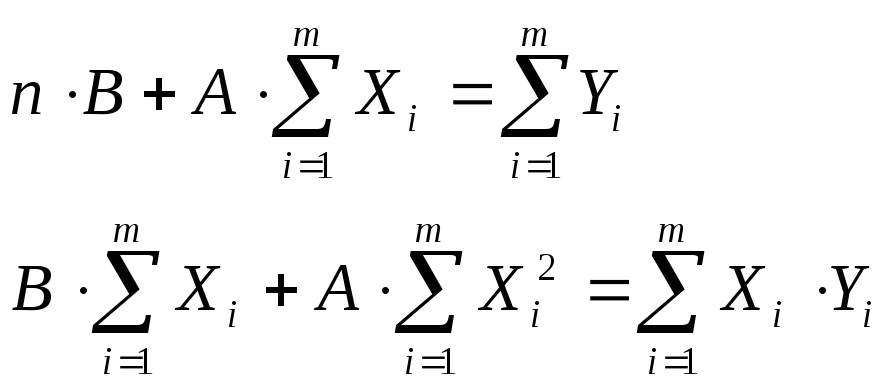
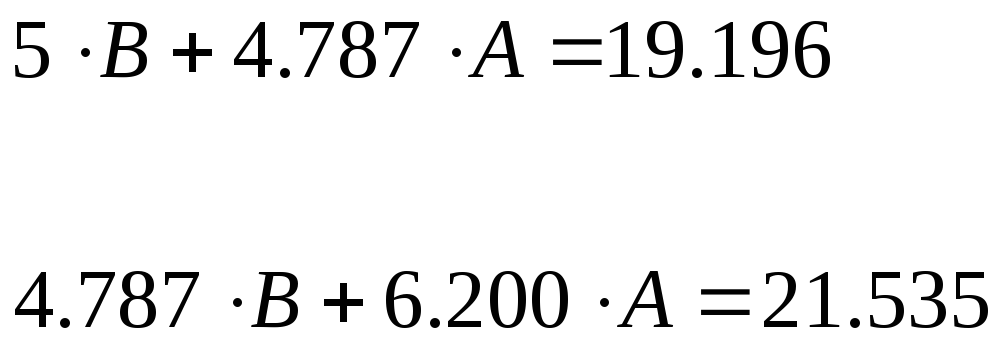
Таким образом
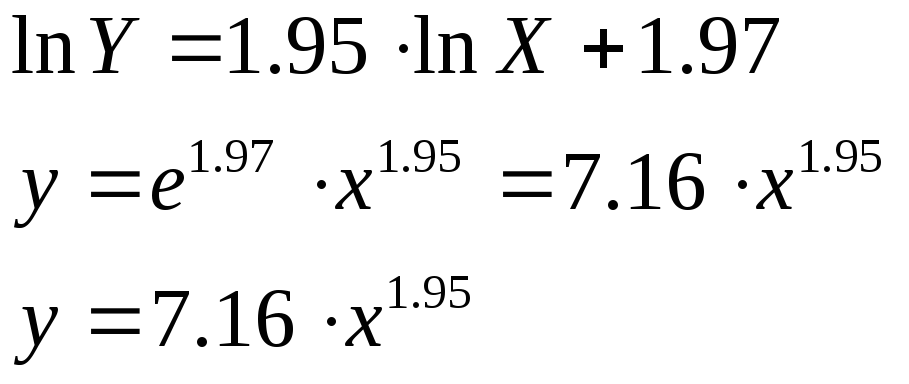
Э
тот
результат можно было бы непосредственно
получить, решая задачу
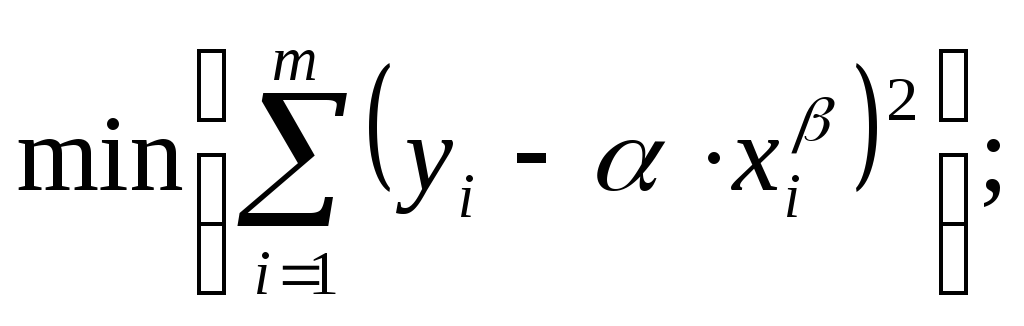
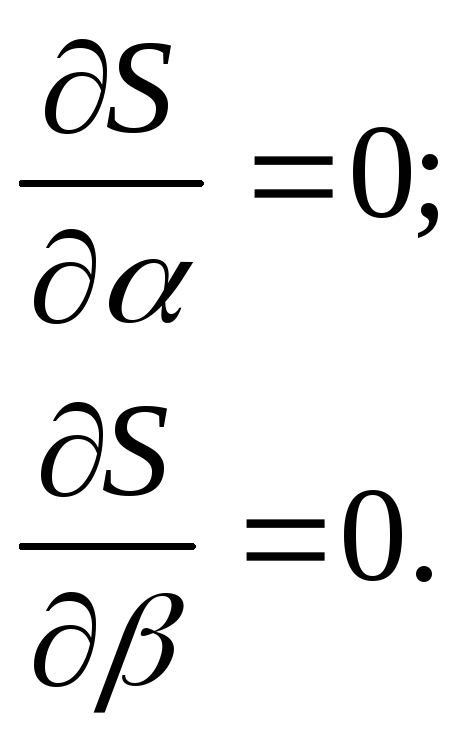
Однако, методом выравнивания задача решается проще!
-
Метод выбранных точек
Обычно применяется для нахождения начальной оценки параметров. Если связь между переменными – нелинейная, то, разлагая нелинейную зависимость в ряд по формуле Тейлора, производят линеаризацию системы, оставляя только линейные члены уравнения. Затем решение уточняется методом итераций. В качестве нулевого (начального) приближения берутся оценки параметров, найденные по методу выбранных точек.
В методе оставляют столько экспериментальных данных, сколько имеется неизвестных параметров.
Затем находится решение полученной системы!