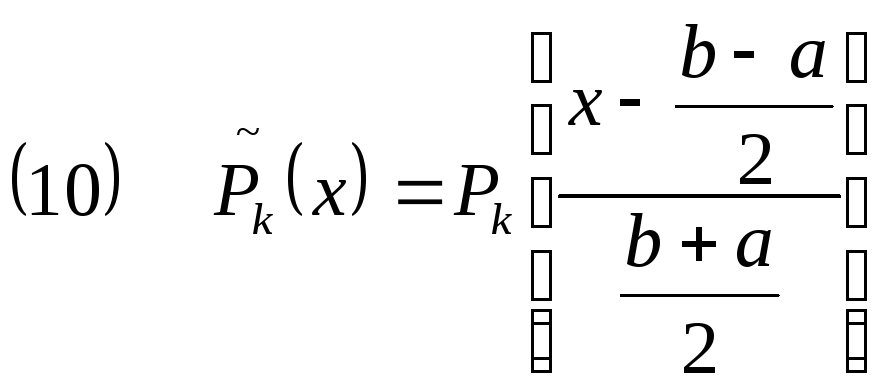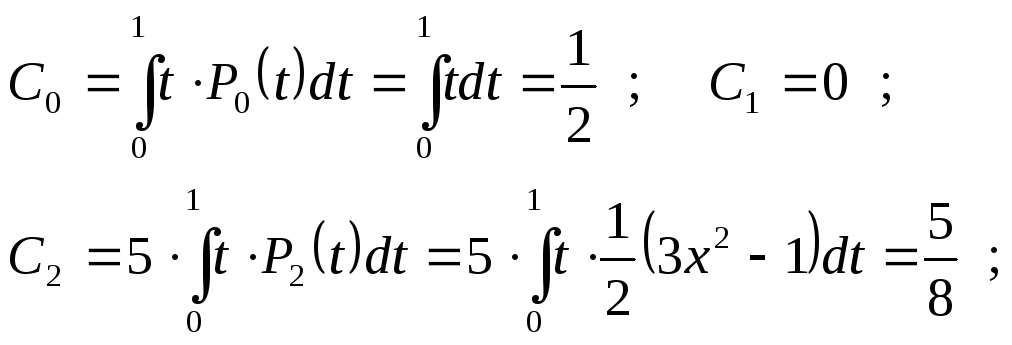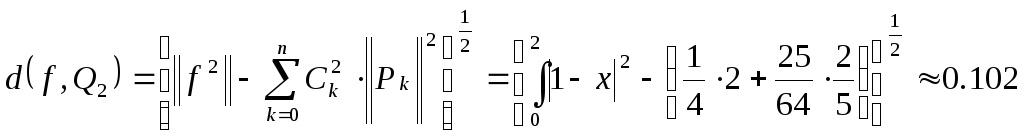- •2202 “Автоматизированные системы обработки
- •Приближенные числа.
- •Действия над приближенными числами.
- •Общая схема метода Гаусса для систем, имеющих единственное решение
- •Обратный ход:
- •Метод Гаусса с выбором максимального элемента по столбцу
- •Достаточное условие сходимости процесса итераций
- •Основные понятия алгебры матриц и теории линейных векторных пространств.
- •Обратная матрица
- •Правило нахождения ранга матрицы:
- •Нахождение обратной матрицы методом Гаусса
- •Применение метода итераций для умножения элементов обратной матрицы
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений
- •Пример:
- •Блок – схема решения уравнения f(X) методом половинного деления
- •Метод хорд
- •Метод Ньютона
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций
- •Теорема
- •Оценка приближения.
- •Интерполирование функций.
- •1. Конечные разности различных порядков.
- •2) Таблица разностей.
- •3) Постановка задачи интерполирования.
- •4) Первая интерполяционная формула Ньютона.
- •Блок-схема построения кубического сплайна
- •Численное дифференцирование
- •2.Конечно-разностные аппроксимации производных.
- •Блок-схема вычисления производной.
- •Численное интегрирование.
- •Блок-схема вычисления определенного интеграла методом двойного пересчета по формуле Симпсона.
- •Квадратурные формулы Гаусса
- •Приближенное вычисление несобственных интегралов с бесконечными пределами.
- •Среднеквадратичное приближение функций
- •Точечное квадратичное аппроксимирование функций
- •Условия нахождения экстремума функции
- •IV Интегральное квадратичное аппроксимирование функций на отрезке.
- •Ортогональные на промежутке системы функций
- •Основные понятия гармонического анализа.
- •4.2.1. Аппроксимация тригонометрическими полиномами кусочно-гладких функций
- •4.3. Среднеквадратичное приближение функций полиномами Лежандра.
- •4.3. Полиномы, наименее уклоняющиеся от нуля.
- •Эмпирические формулы
- •Численное решение обыкновенных дифференциальных уравнений.
- •Численное решение дифференциальных уравнений и систем дифференциальных уравнений высших порядков
- •Численные методы безусловной оптимизации.
4.2.1. Аппроксимация тригонометрическими полиномами кусочно-гладких функций

Функция
![]() называется кусочно-гладкой на отрезке
называется кусочно-гладкой на отрезке
![]() ,
если этот отрезок можно разбить на
конечное число отрезков, в каждом из
которых
,
если этот отрезок можно разбить на
конечное число отрезков, в каждом из
которых
![]() – гладкая функция, т.е.непрерывна вместе
со своей первой производной.
– гладкая функция, т.е.непрерывна вместе
со своей первой производной.
|
Теорема |
Тригонометрический
ряд Фурье кусочно-гладкой функции
В обеих граничных
точках сумма ряда равна среднему
арифметическому ее предельных значений
в этих точках, т.е.
|
||||
|
Пример |
Найти ряд Фурье для функции
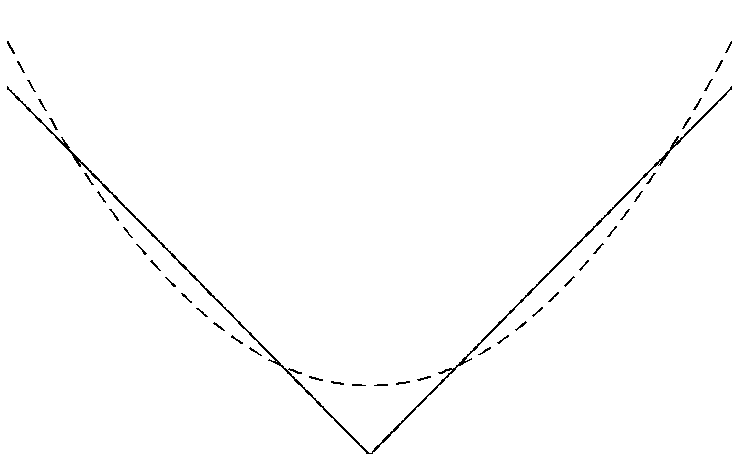
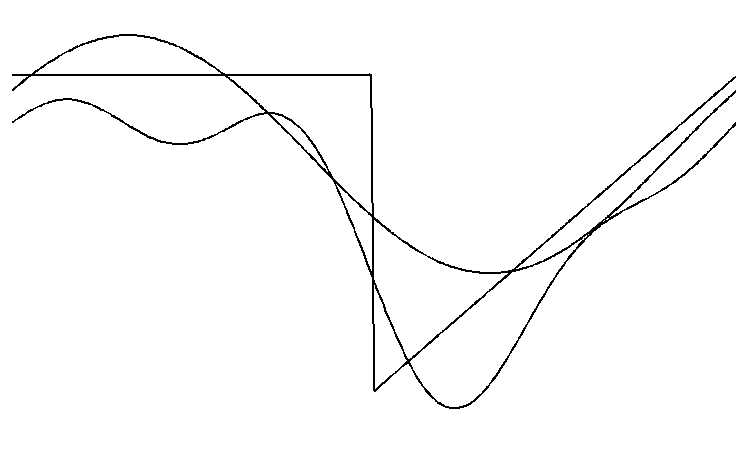
Представить графически
приближение этой функции с помощью
тригонометрических многочленов
степеней
|
||||
|
Решение |
Определяем коэффициенты Фурье (по формуле (4))
Сделаем
замену переменных :
Тогда
и формулы (3), (4) примут вид:
Т.е. (3), (4) и (3'), (4') эквивалентны! Считать удобнее по формулам (3'), (4').
Определяем коэффициенты Фурье (у нас
Т.о. ряд Фурье имеет вид
Многочлен наилучшего приближения получаем из последней формулы:
Погрешность приближения находим по формуле:
(
следует из
т.к.
т
|
4.3. Среднеквадратичное приближение функций полиномами Лежандра.
Многочлены Лежандра определяются следующими формулами
![]()
Дифференцирую, находим:
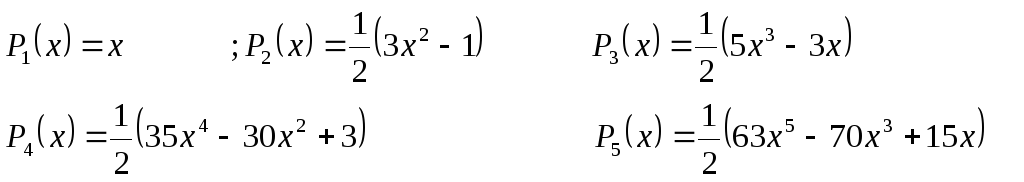
Обобщенный многочлен степени
![]() относительно
системы алгебраических многочленов
Лежандра
относительно
системы алгебраических многочленов
Лежандра
![]() имеет
вид
имеет
вид
![]()
где
![]() – некоторые постоянные.
– некоторые постоянные.
Система многочленов Лежандра
![]() ортогональна на отрезке
ортогональна на отрезке
![]()
![]()
Среднеквадратичная форма![]() :
:
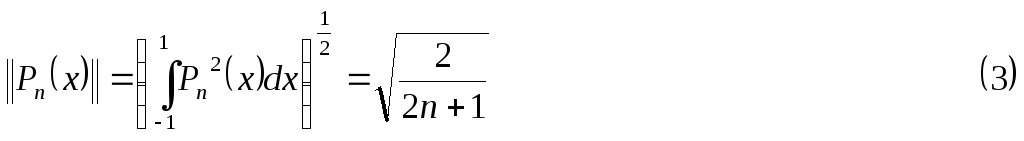
Например:
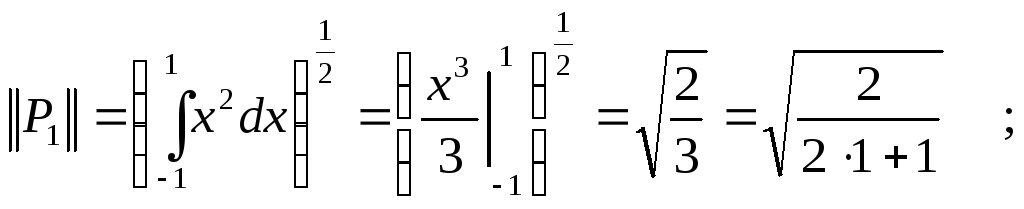
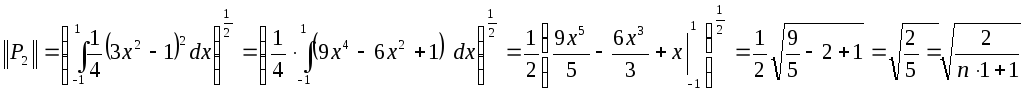
Наилучшее приближение функции
![]() многочленом
многочленом
![]() получается
с коэффициентами Фурье:
получается
с коэффициентами Фурье:
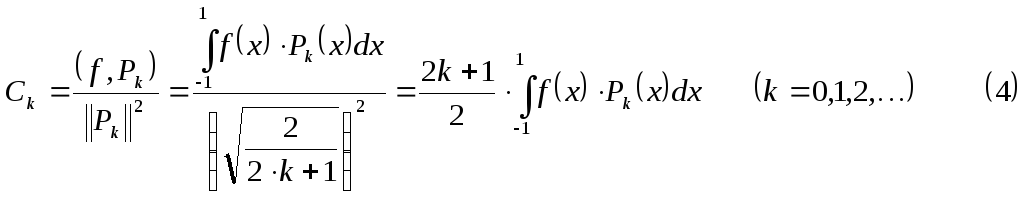
Среднеквадратичное отклонение
аппроксимирующего многочлена от функции
![]() ,
равное
,
равное
![]() ,
в нашем случае определяется равенством
,
в нашем случае определяется равенством

Из формулы
![]() видно,
что
видно,
что
![]() четны при четном
четны при четном
![]() и нечетны при
и нечетны при
![]() нечетном.
нечетном.
Для четной на интервале
![]() функции
функции
![]() коэффициенты Фурье равны:
коэффициенты Фурье равны:
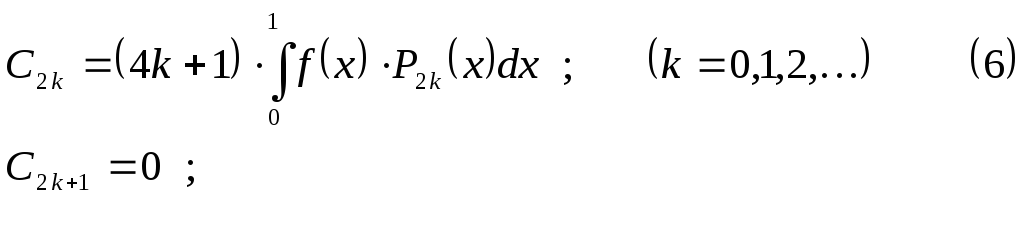
Для нечетной на интервале
![]() функции получаем:
функции получаем:
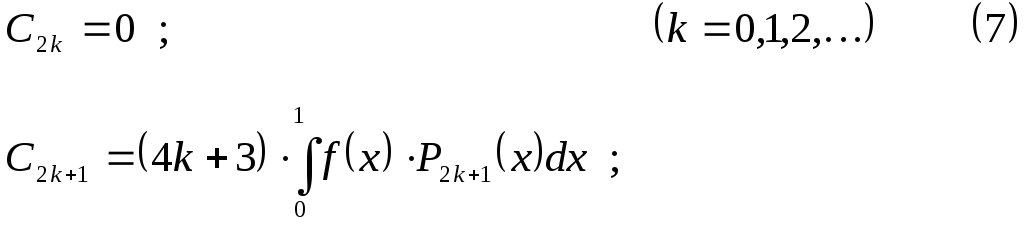
Рядом Фурье – Лежандра называется ряд
![]()
Ряд Фурье – Лежандра сходится к
![]() в среднеквадратичном на отрезке
в среднеквадратичном на отрезке
![]() .
.
|
Теорема |
Р
|
Если
![]() определена на отрезке
определена на отрезке
![]() ,
то с помощью линейного преобразования
,
то с помощью линейного преобразования
![]()
Можно получить многочлены Лежандра,
ортогональные на отрезке
![]() :
:
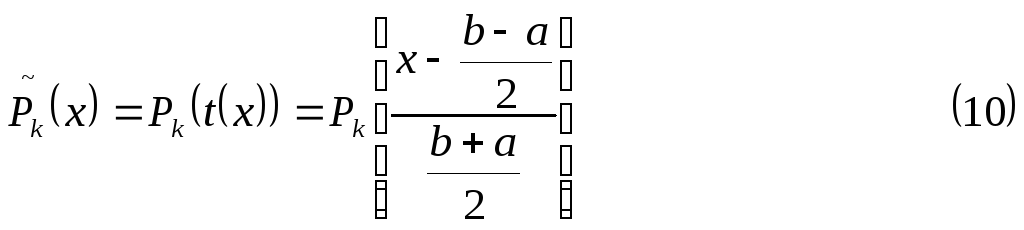
При этом норма
![]() будет равна
будет равна
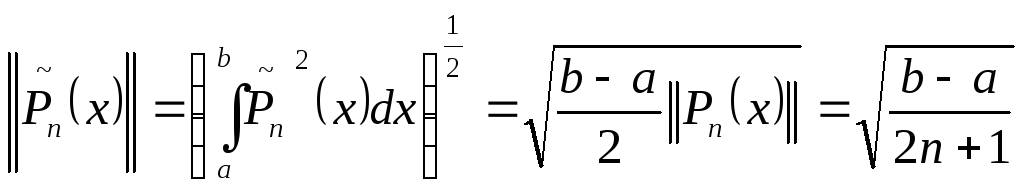
А коэффициенты
![]() примут
вид
примут
вид
![]()
где
![]()
|
Пример |
Найти
алгебраический многочлен степени
Оценить погрешность
|
|
Решение |
Имеем
Используя
формулы:
Находим:
Производя
замену переменной по формуле
Коэффициенты
Фурье вычисляются по формуле
Т.к.
Следовательно
Откуда:
По
формуле
y 2 0
|

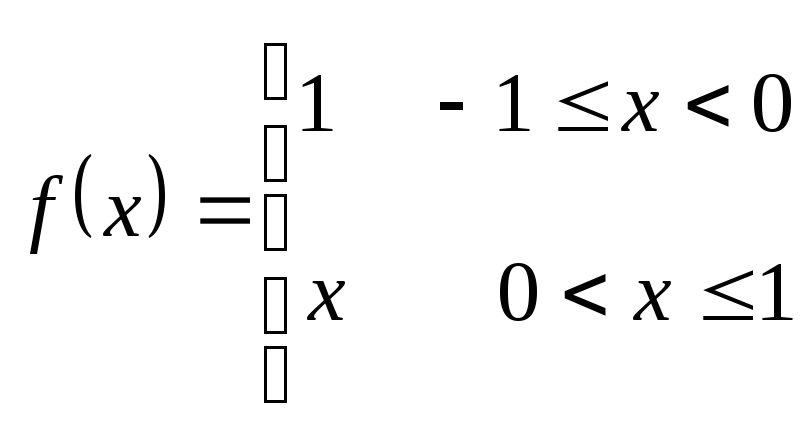
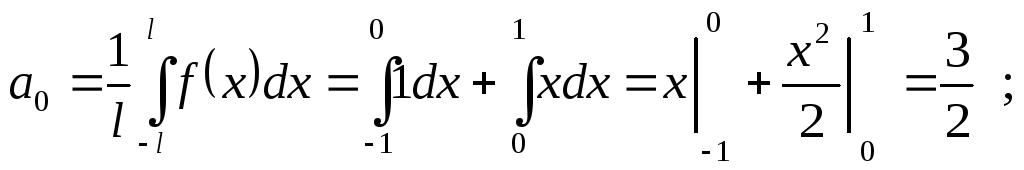
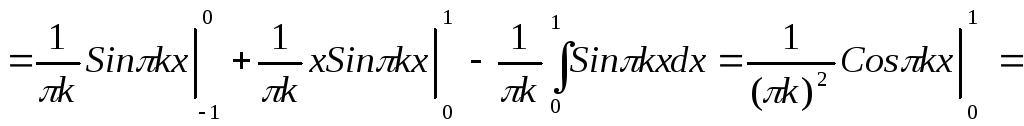
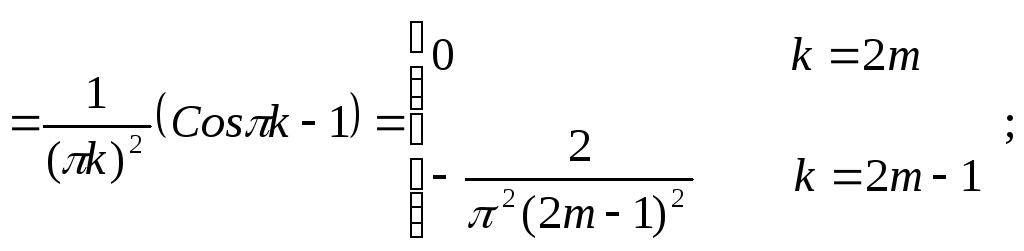
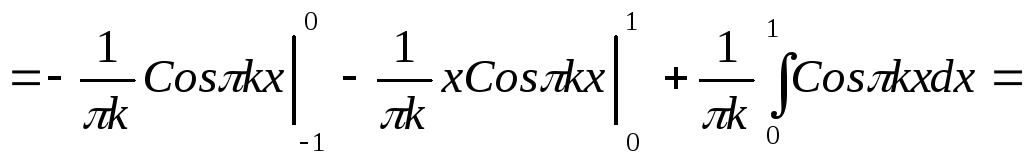
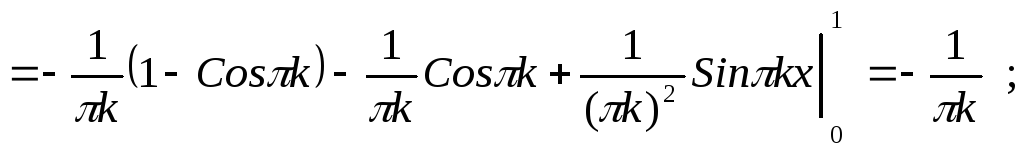
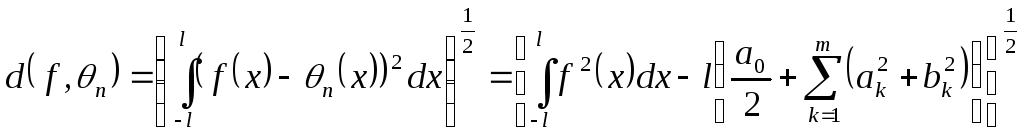
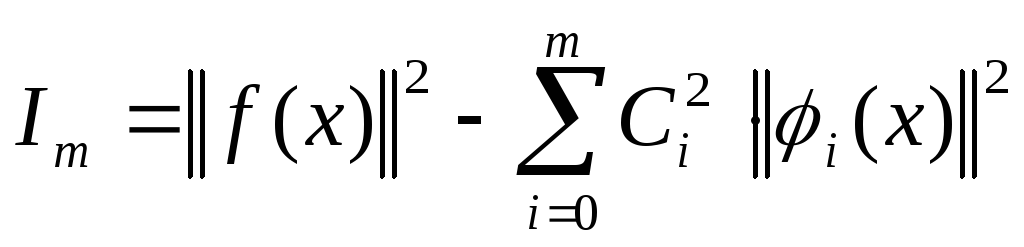 )
)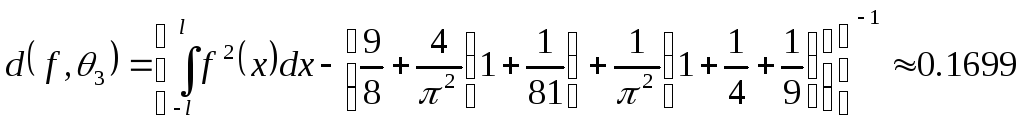
 о
о
 яд
Фурье – Лежандра кусочно-гладкой
функции
яд
Фурье – Лежандра кусочно-гладкой
функции