IV Интегральное квадратичное аппроксимирование функций на отрезке.

До сих пор мы рассматривали аппроксимацию точечных множеств. Теперь рассмотрим аппроксимацию ф-ий на отрезке (непрерывные множества).

За меру отклонения ф-ии f(x) от полинома на отрезке [a,b] принимается величина

Решение ищется из условия минимизации т.е. приравниваются нулю все частные производные . В результате получаем систему уравнений:

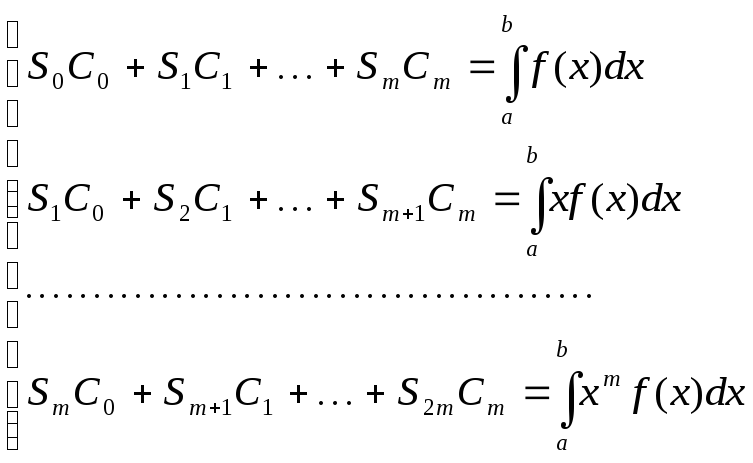(1)

где (k=0,1,2,…,m)

Решение единственное решение, обеспечивающее минимум.

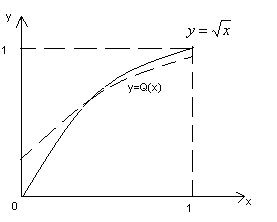
Пример: Найти наилучшую квадратичную аппроксимацию посредством полинома второй степени ф-ии на отрезке [0,1]. Решение:

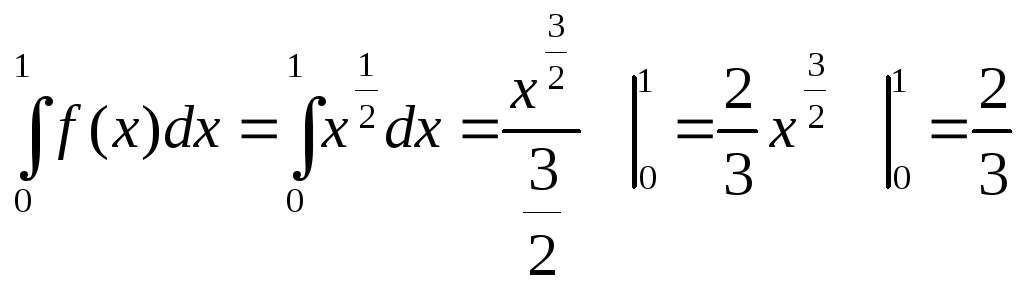
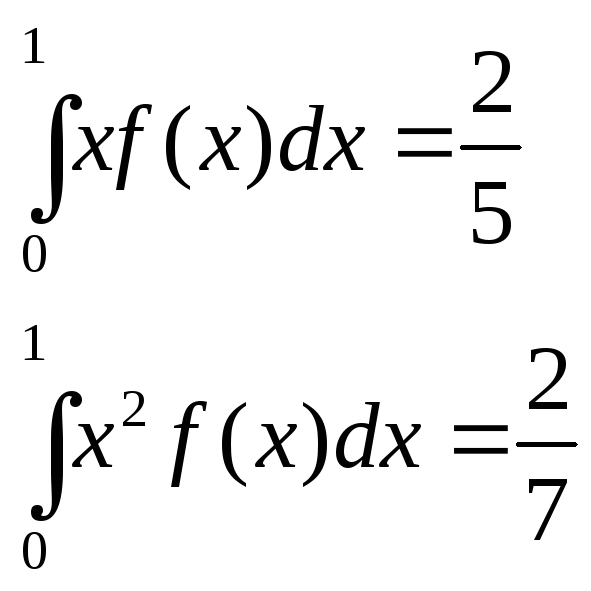Система (1) примет вид:

С=[6/35; 48/35; -4/7]; ; Q(0)=6/35; Q(1)=6/35+48/35-4/7=34/35

Если - обобщенный полином, то

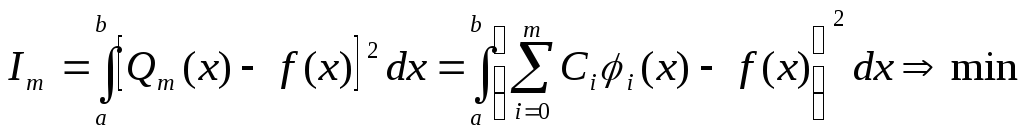
Система (1) в этом случае примет вид:

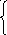
C₀ (φ₀, φ₀) + C₁ (φ₁, φ₀) +…+ C_n (φ_n, φ₀) = (f, φ₀)

C₀ (φ₀, φ₁) + C₁ (φ₁, φ₁) +…+ C_n (φ_n, φ₁) = (f, φ₁) (2)

C₀ (φ₀, φ_n) + C₁ (φ₁, φ_n) +…+ C_n (φ_n, φ_n) = (f, φ_n)

Где

Неудобство интегральной квадратичной аппроксимации - необходимость вычисления определенных интегралов.

В этом случае способ точечной квадратичной аппроксимации предпочтительнее.

1. Ортогональные на промежутке системы функций

Если , при m<>n,

То - система ф-ий, ортогональных (1) на [a,b]

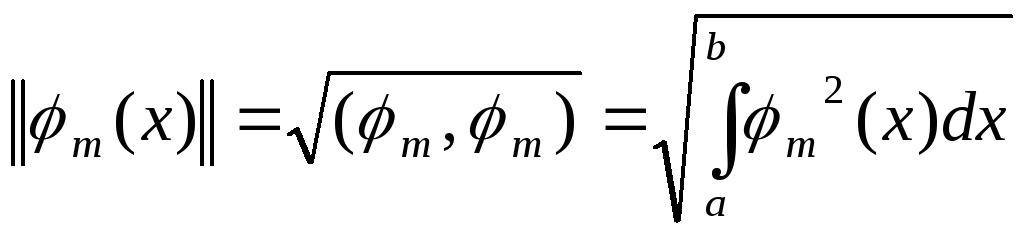- норма ф-ий на [a,b]

Если нормы всех ф-ий системы (1) равны единицы, то это система называется ортонормированной.

Для ортонормированных систем

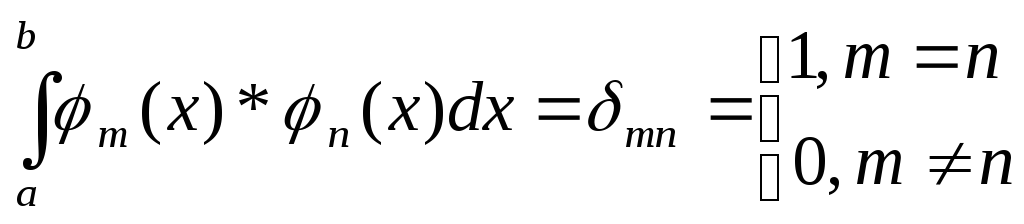
Чтобы любую систему, не содержащую функцийй с нулевой нормой, пронормировать, необходимо каждую функцию разделить на ее норму:

Если система ф-ий ортогональна на отрезке [a,b], то коэффициенты обобщенного полинома

, аппроксимирующего непрерывную ф-ию f(x)на [a,b]

Имеют вид:

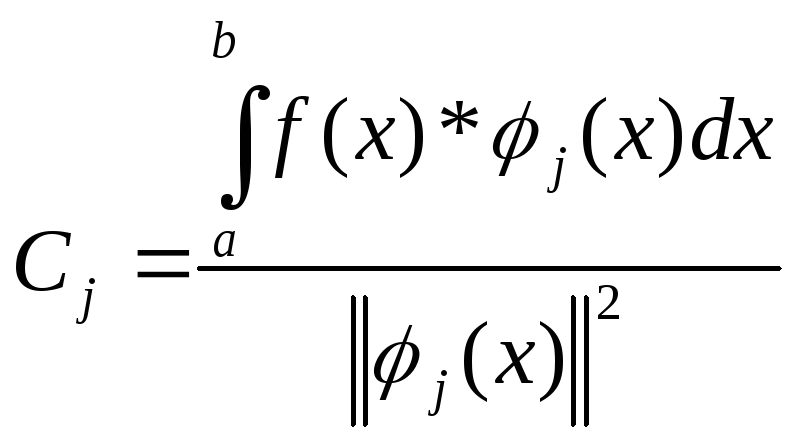
(2) -коэфф. Фурье ф-ии f(x) относительно заданной ортогональной системы .

Обобщенный полином с коэффициентом Фурье данной ф-ии обладает наименьшим квадратичным отклонением от этой ф-ии по сравнению со всеми другими обобщенными полиномами того же порядка m.

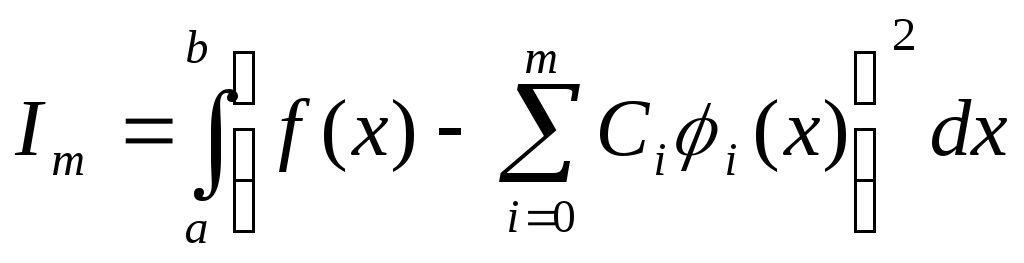(3)

После преобразований (раскрывая скобки, меняя местами и и приводя подобные члены) получим(без вывода):

(4)

(5)

Из (3) следует, что , потому из (5) получаем:

(6) –неравенство Бесселя

П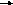ри m ∞

(7)

Если система -ортонормированная, то (8)

Если , то система наз. ПОЛНОЙ.

Для полной ортонормированной системы имеет место равенство Парсеваля

(9)

Свойства обобщенного полинома с коэффициентами Фурье:

1. при увеличении числа слагаемых m младшие коэффициенты остаются неизменными, т.е. при добавлении новых членов прежние коэффициенты не пересчитываются (это следует (2)).

2. при увеличении m квадратичная погрешность монотонно убывает в широком смысле, т.е. Т.о. присоединение новых слагаемых увеличивает точность аппроксимации.

2. Основные понятия гармонического анализа.

Тригонометрическая система функций:

1, sin x, cos x, sin 2x, cos 2x,…, sin nx, cos nx (1)

ортогональна на любом отрезке длины 2π (напрмер, на [-π, π]).

Нормы функций системы (1)

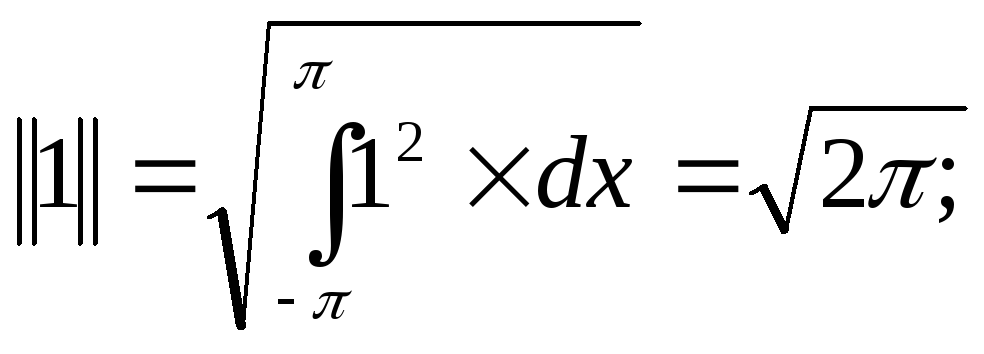
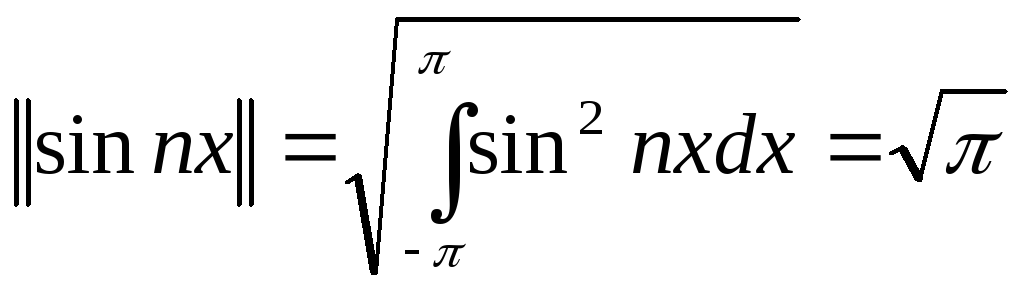
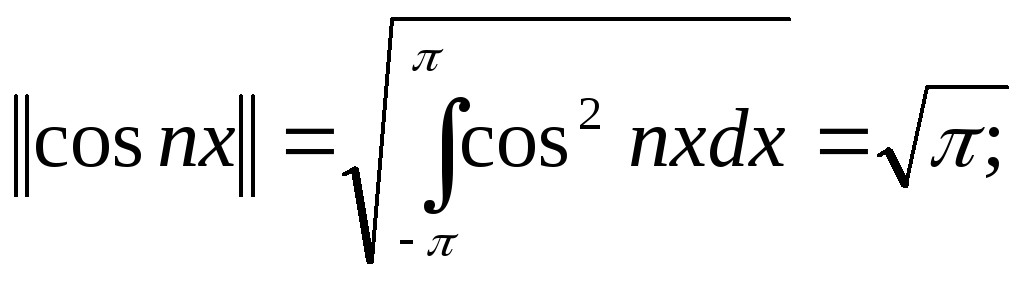n=1,2…. (2)

Пусть дана непрерывная периодическая функция с периодом 2π (введением новой переменной можно область определения функции [a, b] перевести в интервал [-π,π])

Составим тригонометрический полином

(3)

Слагаемые k=1,2…, называются гармонитами.

Чтобы минимизировать

min

Коэффициенты , , должны быть коэффициентами Фурье функции f(х) относительно системы (1)

т.е.

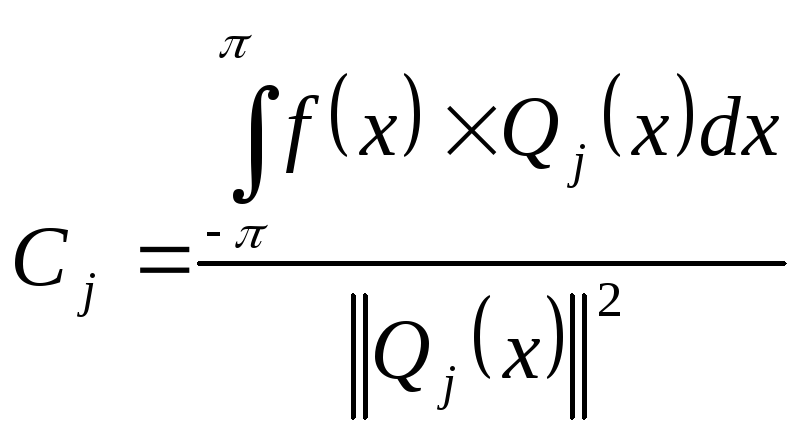
Т.о. получаем:

(4)

(k=0,1,2,…m)

Полином (3) – тригонометрический полином Фурье;

, - тригонометрические коэффициенты Фурье функции f(х).

Если f(х) четная, то

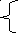(k=1,2,…,m)

k=0,1,2…m (5)

Если f(х) нечетная, то

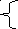(k=0,1,2,…,m)

(k=1,2,…,m) (6)

Для четной функции

-

При m→∞ получаем тригонометрический ряд Фурье

Представленные функции тригонометрическим полиномом Фурье или тригонометрическим рядом Фурье называется гармоническим анализом.

В простейших случаях коэффициенты тригонометрического полинома Фурье вычисляются непосредственно по формулам (4)

Среднеквадратическое отклонение определено как

,

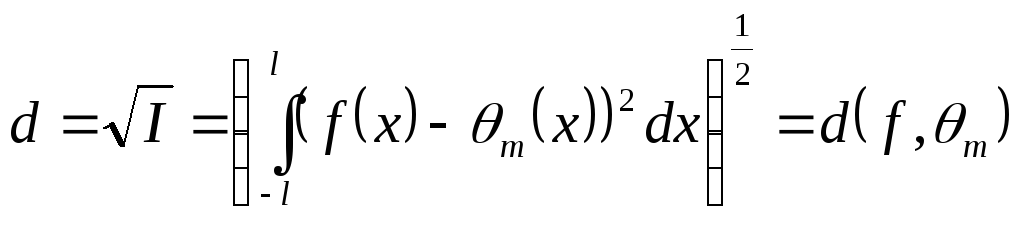в общем случае функция задана на интервале .