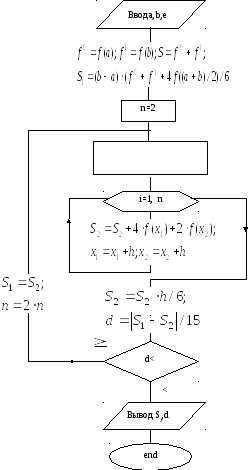
Блок-схема вычисления определенного интеграла методом двойного пересчета по формуле Симпсона.

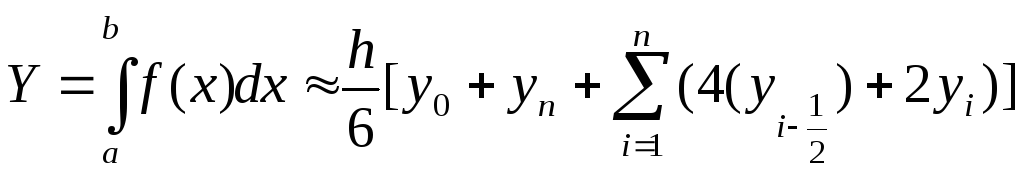
ЛЕКЦИЯ 13

Численное интегрирование (продолжение)

Квадратурные формулы Гаусса

Пусть отрезок интегрирования непрерывной функции f(x) разбит на n равных частей точками . Шаг разбиения . Пусть - функция аппроксимирующая подынтегральная функцию f(x).

На каждом из интервалов расположено m узлов , в которых . Пусть - многочлен степени р, такой что

а) ; ;

б) Определенный интеграл от функции на отрезке выражается через значение подынтегральной функции в узлах в виде их линейной комбинации т.е.

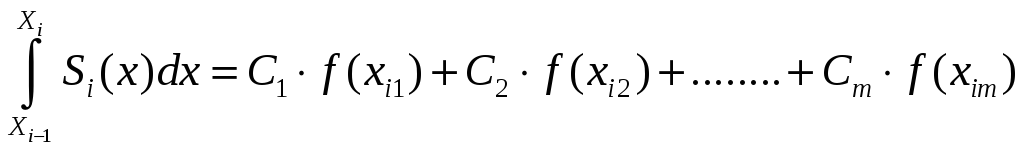(1)

Так чтобы для выбранной степени р сплайна построить квадратурные формулы Гаусса , необходимо найти из условий а) и б) 2m неизвестных:

m неизвестных коэффициентов

m координат узлов ()

Будем решать задачу одновременно для всех участков . Для этого введем новую переменную t, общую для всех интервалов.

Тогда: , и

И при т.о.

Положим:

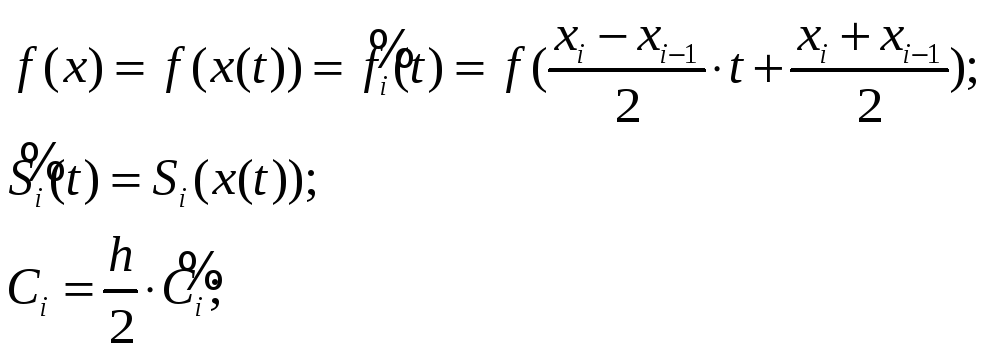
Тогда:

и (1) примет вид:

(2)

Теперь рассмотрим квадратную формулу Гаусса с тремя узлами (m=3). При этом необходимо определить шесть величин:

Функция -многочлен степени р.

(3)

Подставим (3) в (2). Учитывая, что получим тождество относительно коэффициентов

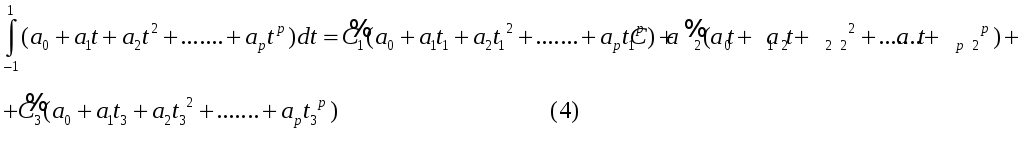
В общем случае степень аппроксимирующего полинома равна: p=2m-1, где m-число узлов.

Для трех узлов имеем р=5, т.е. многочлен пятой степени. Коэффициенты при вычисляем из левой части (4)

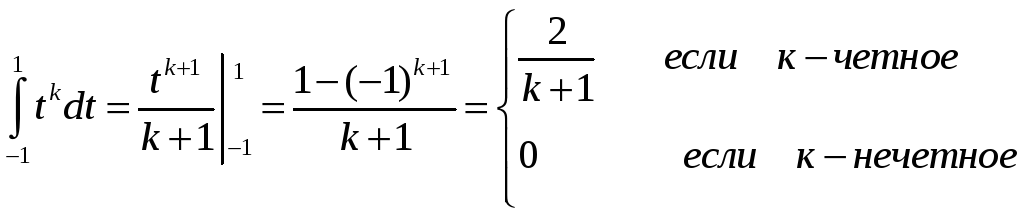(5)

Приравнивая коэффициенты при в правой и левых частях и учитывая (5), получим шесть уравнений:

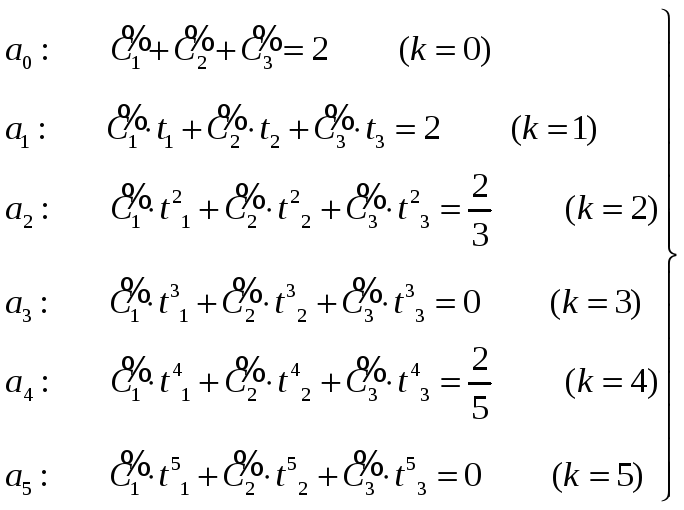(6)

Решение системы (6) – нелинейной системы найти очень сложно!

Однако оказывается, что неизвестное в уравнениях (6) совпадают с нулями многочлена Лежандра:

(7)

Нули многочлена (7) принадлежат интервалу и расположены симметрично середины интервала.

В нашем случае m=3:

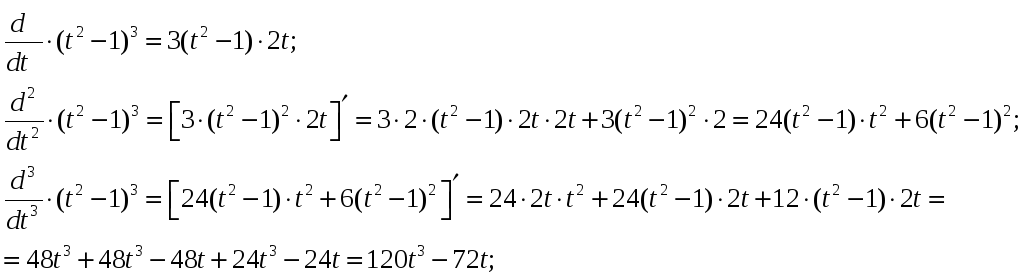
т.о.

Корни (нули) уравнения находим из:

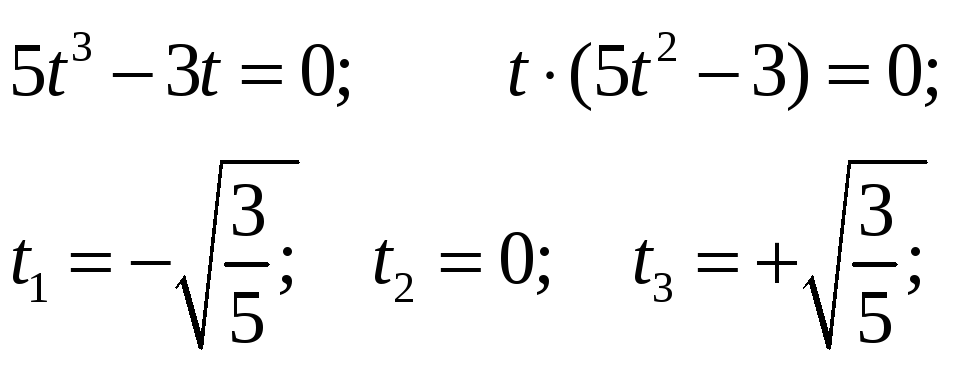
Т.о. найдены значения системы (6)

Значения находим, подставляя в (6)

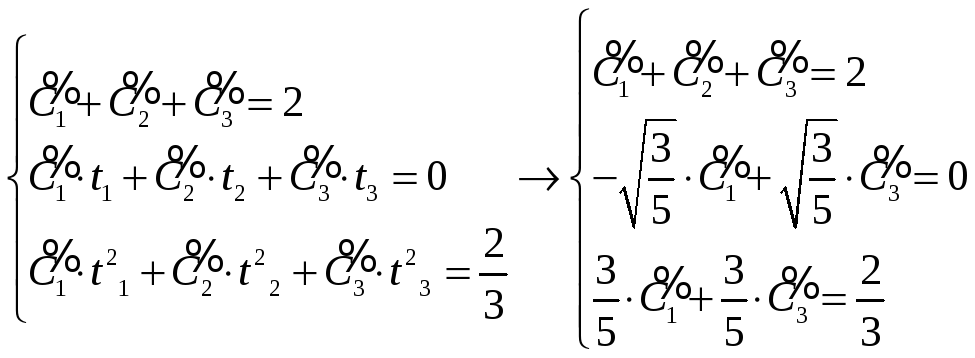
Решение системы:

Подставим найденные значения в (1):

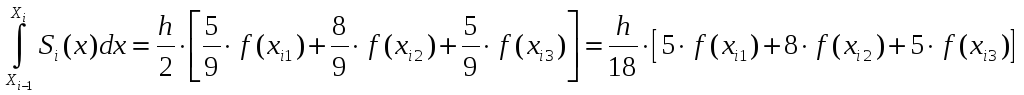
находим из

находим с учетом соотношения:

Т.о.

Для получаем:

Т.о.

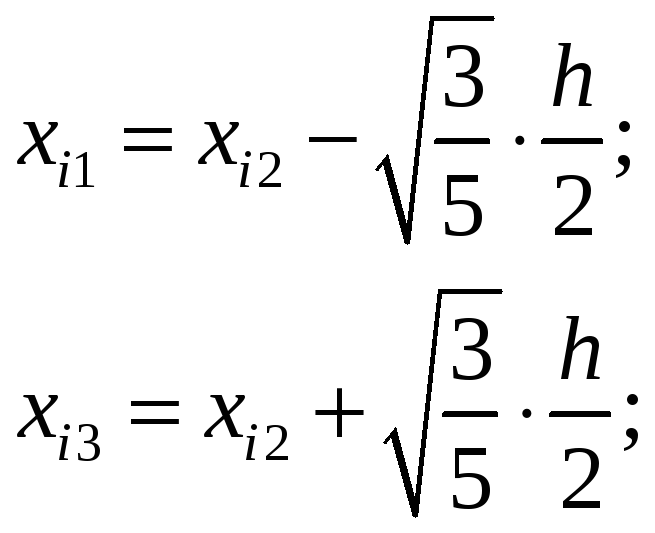
Итак, квадратичная формула Гаусса с тремя узлами имеет вид:

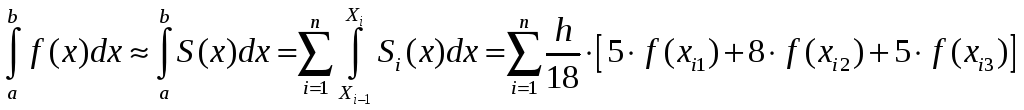
Где

Если имеет непрерывность производной до шестого прядка, то для оценки погрешности формулы Гаусса с тремя узлами можно использовать неравенство:

При вычислении интеграла до достижения заданной точки Е методом двойного перечета,

условие окончаний вычисления имеет вид:

Где k=2m, m-число узлов.

При этом полагают, что

с точностью Е

Пример: Найти приближенное значение интеграла по квадратной формуле Гаусса с тремя узлами для n=1, т.е. без разбиения отрезка на части (n=1)

Оценить погрешность вычислений.

Решение. Ищем:

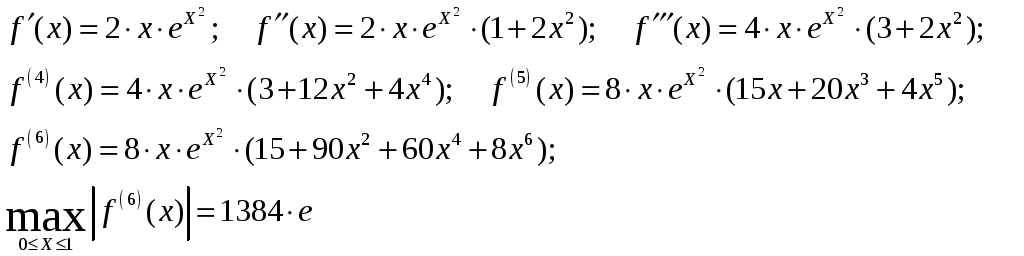
R(h)

а ≤ х ≤ в

С погрешностью не больше чем 0,0019<0,002 имеем

Здесь х₂ = 0,5; f(x₂) = 1.284025

x₁ = x₂ - f(x₁) = 1.012783

x₃ = x₂ - f(x₁) = 2.19745

Для достижения точности того же порядка с использованием: формулы Симпсона n=2 (ε=0,0045)

формулы прямоугольников n=10 (0,0068)

ЛЕКЦИЯ 14