Блок-схема вычисления производной.

Ввод х,е

=0,1; a=10 ; y’₀ =y(x, )

=/a; y’₁=y(x, ); e₁=

<

ЛЕКЦИЯ 12

Численное интегрирование.

S=.Разобьем отрезок [a,b] на n равных частей.

Обозначим:

Заменим y=f(x) …… кусочно-полиномиальной функцией S(x) аппроксимирующей данную функцию. Интегрируя S(x) на отрезке [a,b], получим формулу численного интегрирования – квадратную формулу.

1)если на каждом интервале [] (i=1,2,…,n.) заменим f(x) ступенчатой функцией

f(x) S(x) = ,

где - середина интервала

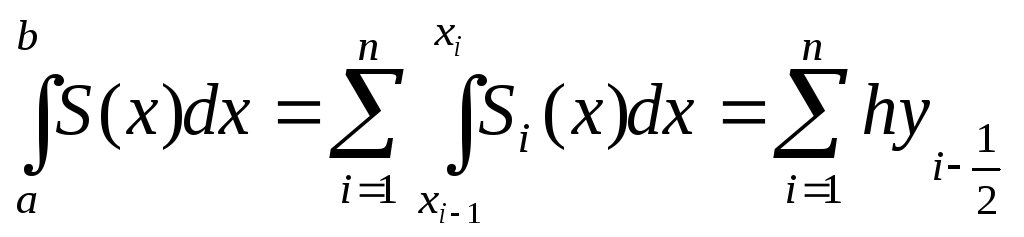тогда т.к

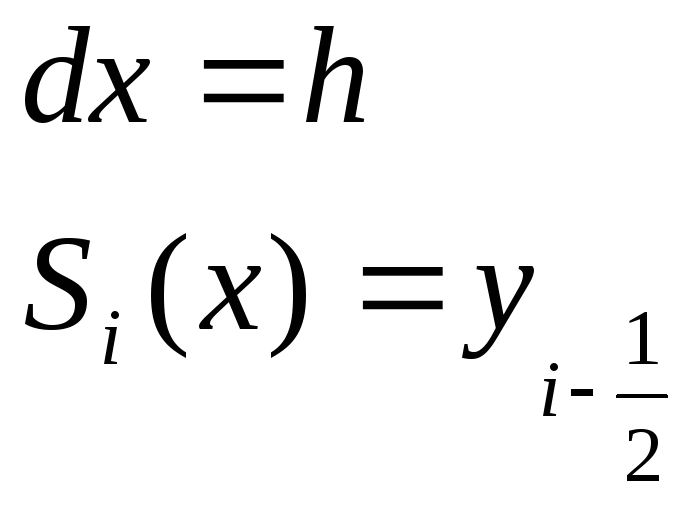
и получаем квадратурную формулу прямоугольников:

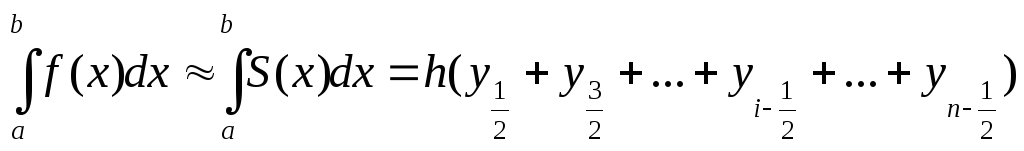(1)

2)Если f(x) на каждом отрезке [] заменить её на линейной интерполяции по точкам , то получим

i=1,…,n

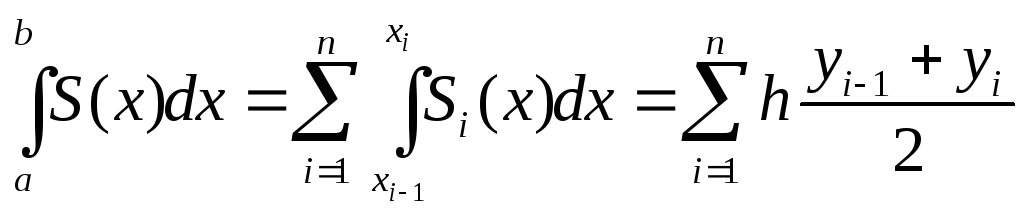i=1,2,…..,n

Действительно:

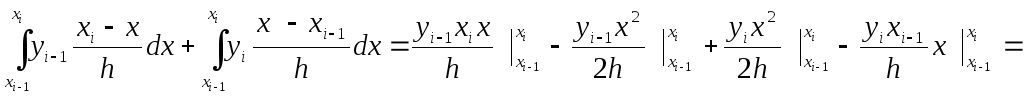
(т.к. ) =

Т.о. получаем квадратурную формулу трапеций:

(2)

3) Если …. S(x) , определяет собой непрерывную функцию , составленную из примыкающих парабол, можно получить квадратурную формулу Симпсона, или формулу парабол.

Пусть на отрезке [] парабола проходит через точки (),(),() . Строим интерполяционный многочлен Лагранжа второго порядка:

(в знаменателе(первый шаг): )

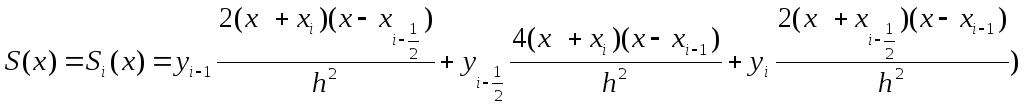
i=1,2,….,n

Введем новую переменную t : t =;

Тогда ; ;

Значениям t= 0, 1/2 , 1 соответствуют значения х ,равные .

и т.д.

Выразим S(x) через новую переменную t:

S(x)= =

= (i=1,2,….,n)

Рассмотрим, например, 1-ый член

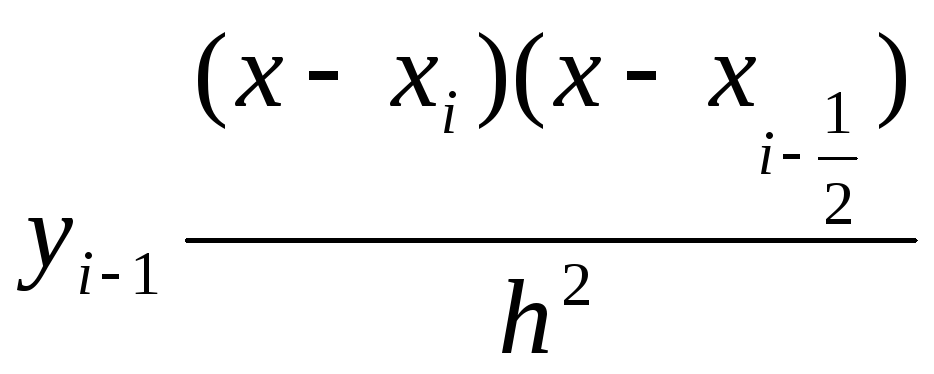
Т.к. , а , получаем:

=

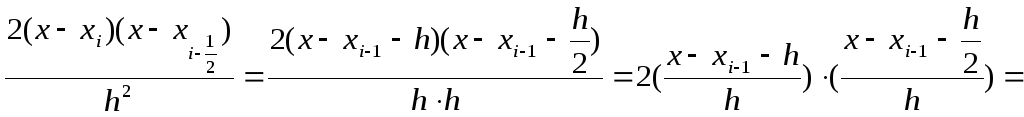
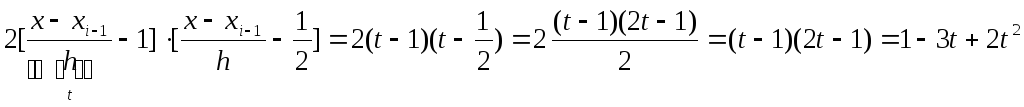
Далее, учитывая, что , получаем:

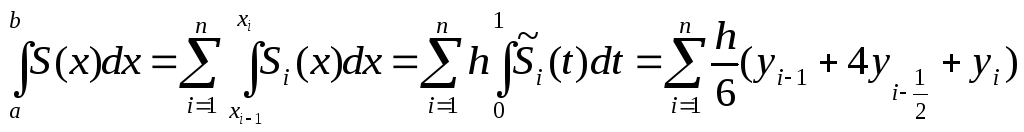
Т.о. имеем квадратурную формулу парабол:

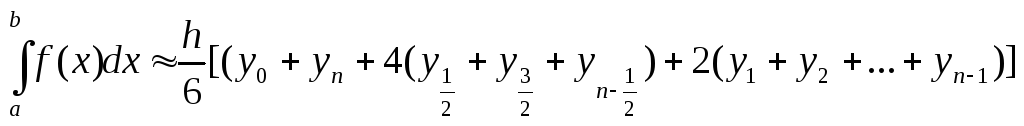(3)

Погрешность каждой квадратичной формулы оценивается величиной остаточного члена R(h), зависящего от шага разбиения h (или от числа разбиений n):

Если f(x) имеет непрерывную производную второго порядка , то получаем:

Для формулы трапеций

Если f(x) имеет непрерывную производную 4-го порядка, то оценка погрешности формулы Симпсона:

Пример:

Найти приближенное значение интеграла с помощью квадратурных формул прямоугольников , трапеций и Симпсона, если отрезок интегрирования [0,1] разбит на n =2; 4 ;10 равных частей. Оценить величину погрешности полученных результатов.

Решение:

Погрешность .

Находим производные f(x):

; ; ;

;

При n=4 получим:

;

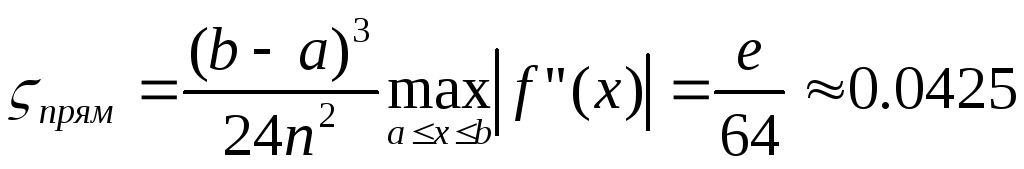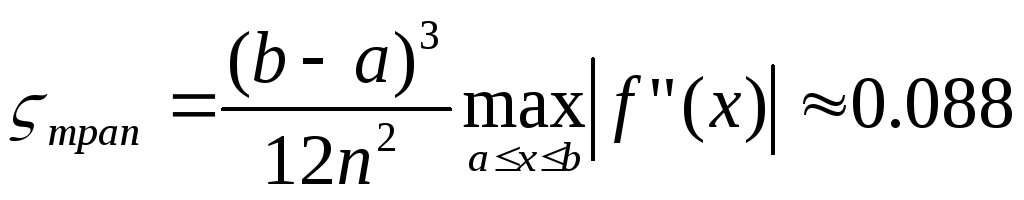
(в 200 раз точнее)

Результаты сведены в таблицу:

формула	n=2		n=4		n=10
	Y (2)		Y (4)		Y (10)
прямоугольник	1.40977	0.1699	1.44875	0.0425	1.46039	0.0068
трапеция	1.57158	0.3398	1.49068	0.085	1.46717	0.0136
Симпсона	1.46371	0.0045	1.46272	0.0003	1.46265

Метод двойного пересчета

Позволяет оценить текущую оценку точности по той или иной квадратурной формуле:

1.проводится вычисления с шагом h и получается (h).

2.шаг h уменьшается вдвое и получается (h/2).

3.используется правило Рунге:

, где Y-точное значение интеграла

K=2 –прямоугольников и трапеции

К=4- для формулы Симпсона

При заданной точности вычисления проводят до окончания приближений при выполнении условия:

при этом полагают