
- •2202 “Автоматизированные системы обработки
- •Приближенные числа.
- •Действия над приближенными числами.
- •Общая схема метода Гаусса для систем, имеющих единственное решение
- •Обратный ход:
- •Метод Гаусса с выбором максимального элемента по столбцу
- •Достаточное условие сходимости процесса итераций
- •Основные понятия алгебры матриц и теории линейных векторных пространств.
- •Обратная матрица
- •Правило нахождения ранга матрицы:
- •Нахождение обратной матрицы методом Гаусса
- •Применение метода итераций для умножения элементов обратной матрицы
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений
- •Пример:
- •Блок – схема решения уравнения f(X) методом половинного деления
- •Метод хорд
- •Метод Ньютона
- •Пример:
- •Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций
- •Теорема
- •Оценка приближения.
- •Интерполирование функций.
- •1. Конечные разности различных порядков.
- •2) Таблица разностей.
- •3) Постановка задачи интерполирования.
- •4) Первая интерполяционная формула Ньютона.
- •Блок-схема построения кубического сплайна
- •Численное дифференцирование
- •2.Конечно-разностные аппроксимации производных.
- •Блок-схема вычисления производной.
- •Численное интегрирование.
- •Блок-схема вычисления определенного интеграла методом двойного пересчета по формуле Симпсона.
- •Квадратурные формулы Гаусса
- •Приближенное вычисление несобственных интегралов с бесконечными пределами.
- •Среднеквадратичное приближение функций
- •Точечное квадратичное аппроксимирование функций
- •Условия нахождения экстремума функции
- •IV Интегральное квадратичное аппроксимирование функций на отрезке.
- •Ортогональные на промежутке системы функций
- •Основные понятия гармонического анализа.
- •4.2.1. Аппроксимация тригонометрическими полиномами кусочно-гладких функций
- •4.3. Среднеквадратичное приближение функций полиномами Лежандра.
- •4.3. Полиномы, наименее уклоняющиеся от нуля.
- •Эмпирические формулы
- •Численное решение обыкновенных дифференциальных уравнений.
- •Численное решение дифференциальных уравнений и систем дифференциальных уравнений высших порядков
- •Численные методы безусловной оптимизации.
3) Постановка задачи интерполирования.
На отрезке
![]() заданы n+1 точки
заданы n+1 точки
![]() ,
которые называются узлами интерполяции,
и значение некоторой функции
,
которые называются узлами интерполяции,
и значение некоторой функции
![]() в этих точках
в этих точках
![]() .
(1)
.
(1)
Требуется построить интерполирующую
функцию F(x),
принадлежащую известному классу и
принимающую в узлах интерполяции те же
значения, что и
![]() ,
т.е.
,
т.е.
![]() (2)
(2)
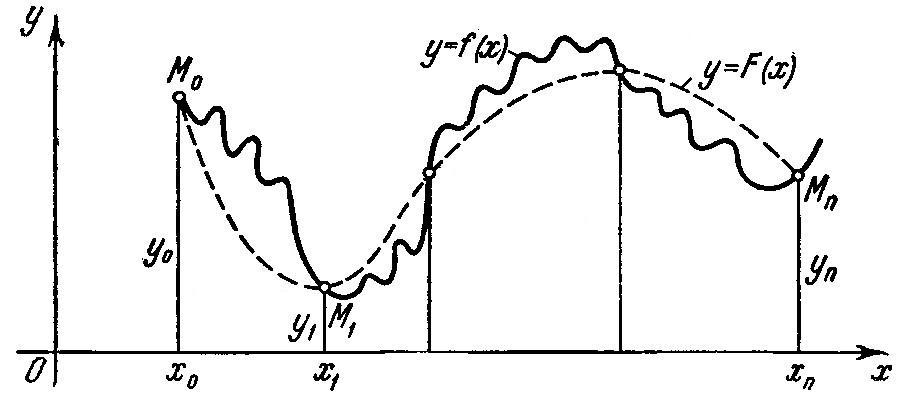
В общем случае, задача имеет бесчисленное множество решений!!!
Задача становится однозначной, если решение искать в заданном классе функций!
Будем искать полином
![]() степени
не выше n и удовлетворяющий
условию (2).
степени
не выше n и удовлетворяющий
условию (2).
Полученную интерполяционную формулу
![]() используют для вычисления значений
используют для вычисления значений
![]() в точках (интервалах), отличных от узлов.
в точках (интервалах), отличных от узлов.
Если
![]() -
имеет место задача интерполирования
(интерполирование “в узком смысле”).
-
имеет место задача интерполирования
(интерполирование “в узком смысле”).
При
![]() решается задача экстраполирования.
решается задача экстраполирования.
4) Первая интерполяционная формула Ньютона.
Пусть для функции
![]() заданы значения
заданы значения
![]() для равноотстоящих узлов
для равноотстоящих узлов
![]()
![]() ,
где
,
где
![]() - шаг интерполяции.
- шаг интерполяции.
Необходимо подобрать полином
![]()
![]() (1)
(1)
Условия (1) эквивалентны тому, что
![]() ,
при
,
при
![]() .
.
Следуя Ньютону, будем искать полином в виде
![]() (2)
(2)
Т.о. задача сводится к определению
коэффициентов
![]()
![]() в выражении (2).
в выражении (2).
Полагая
![]() ,
получим
,
получим
![]() .
.
Далее находим первую конечную разность
![]() и
полагая
и
полагая
![]() ,
получим
,
получим
![]()
Откуда:
![]()
Беря затем вторые разности и т.д., получаем:
![]()
![]()
Введем в рассмотрение новую переменную
![]() -
число шагов, необходимых для достижения
точки
-
число шагов, необходимых для достижения
точки
![]() из точки
из точки
![]()
(![]() ),
получим
),
получим
![]() (3)
(3)
первая интерполяционная формула Ньютона,
которая применяется для интерполирования
функций
![]() ,
в окрестности начального значения
,
в окрестности начального значения
![]() ,
где q мало по абсолютной
величине!
,
где q мало по абсолютной
величине!
Если в (3) положить n=1, то получим формулу линейного интерполирования
![]() (4)
(4)
При n=2 – формулу параболического или квадратичного интерполирования.
![]()
Если дана неограниченная таблица
![]() ,
то n выбирают так, чтобы
,
то n выбирают так, чтобы
![]() .
.
Если таблица конечна, то n не может превышать k-1, где k – число строк таблицы.
При применении 1-ой интерполяционной формулы Ньютона удобно пользоваться горизонтальной таблицей разностей.
Пример: Построить на отрезке [3,5;3,7]
интерполяционный полином Ньютона для
функции
![]() ,
заданной таблицей, с шагом h=0,05.
,
заданной таблицей, с шагом h=0,05.
|
|
3,50 |
3,55 |
3,60 |
3,65 |
3,70 |
|
|
33,115 |
34,813 |
36,598 |
38,475 |
40,447 |
Решение: составляем таблицу разностей
|
|
|
|
|
|
|
3,50 3,55 3,60 3,65 3,70 |
33,115 34,813 36,598 38,475 40,447 |
1,698 1,785 1,877 1,972 |
0,087 0,092 0,095 |
0,005 0,003
|
Т.к.
![]() то n=3.
то n=3.
![]()
![]() или
или
![]()
где
![]()
Можно упорядочить полином по степеням х, подставив значение q.
ЛЕКЦИЯ 9
Интерполирование функций. (Продолжение)
Вторая интерполяционная формула Ньютона.
Для интерполирования функции в конце таблицы применяется вторая интерполяционная формула Ньютона.
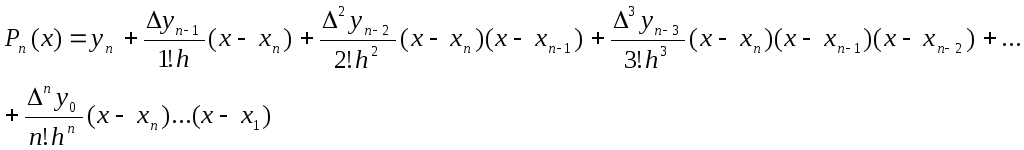 (1)
(1)
Вывод формулы аналогичен 1-ой
интерполяционной формуле, только теперь
коэффициент полинома
![]() (коэффициент
(коэффициент
![]() )
определяется из равенств
)
определяется из равенств
![]() (2)
(2)
![]()
Введем обозначение
![]()
Тогда
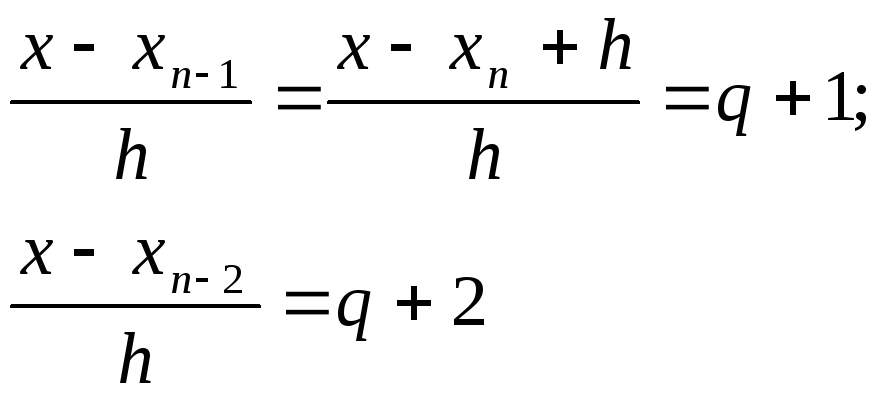
и так далее.
В результате получим:
![]() (3)
(3)
Пример: дана таблица значений
![]() семизначных логарифмов:
семизначных логарифмов:
|
х |
У |
|
1000 1010 1020 1030 1040 1050 |
3,0000000 3,0043214 3,0086002 3,0128372 3,0170333 3,0211893 |
Найти lg1044
Решение: составляем таблицу конечных разностей.
|
|
|
|
|
|
|
1000 1010 1020 1030 1040 1050 |
3,0000000 3,0043214 3,0086002 3,0128372 3,0170333 3,0211893 |
43214 42788 42370 41961 41560 |
-426 -418 -409 -401 |
8 9 8 |
Примем
![]() Тогда
Тогда
![]() .
.
По формуле (3) получаем:
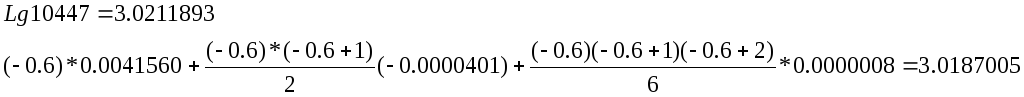 В результате все знаки верные!
В результате все знаки верные!
Т.о. первая интерполяционная формула Ньютона применяется для интерполирования вперед и экстраполирования назад ( за границы интервала); Вторая формула – для интерполирования назад и экстраполирования вперед.
Операция экстраполирования менее точна!
Оценки погрешностей интерполяционных формул Ньютона.
Если узлы интерполирования
![]() - равноотстоящие причем
- равноотстоящие причем
![]()
![]() то , пологая
то , пологая
![]() ,
получим остаточные члены для 1-ой и 2-ой
интерполяционных формул Ньютона:
,
получим остаточные члены для 1-ой и 2-ой
интерполяционных формул Ньютона:
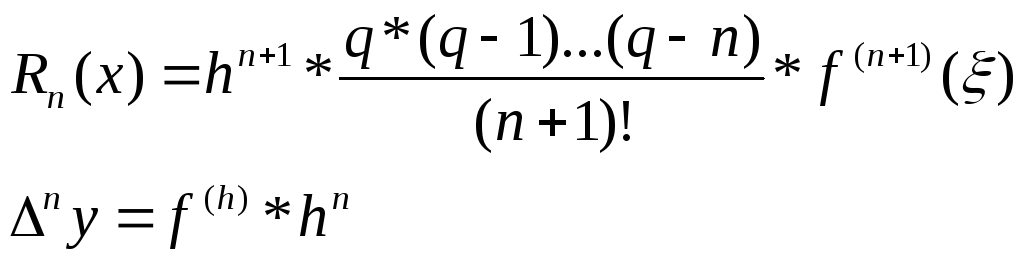 (1)
(1)
![]() , (2)
, (2)
Где
![]() -
некоторое промежуточное значение между
узлом интерполирования
-
некоторое промежуточное значение между
узлом интерполирования
![]() и точкой
и точкой
![]() .
.
(Для интерполирования
![]() ,
для экстраполирования возможно, что
,
для экстраполирования возможно, что
![]() ).
).
При расчетах порядок n
разностей выбирается таким, что
![]() .
Учитывая, что h достаточно
мало и
.
Учитывая, что h достаточно
мало и
![]() и что
и что
![]()
можно положить:
![]() (3)
(3)
При этом остаточные члены интерполяционных формул Ньютона будут равны ( подставляя (3) в (1) и (2) ).
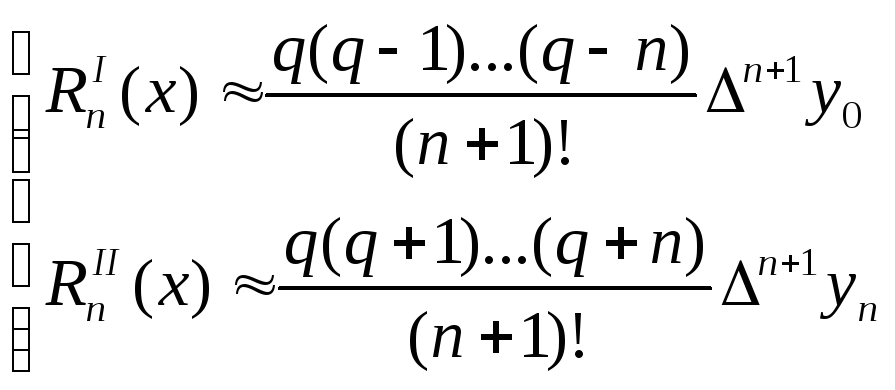
Пример: В пятизначных таблицах
логарифмов даются логарифмы целых
чисел от х=1000 до х=10000 с предельной
абсолютной погрешностью, равной
![]() .
Возможно ли линейное программирование
с той же степенью точности?
.
Возможно ли линейное программирование
с той же степенью точности?
Решение: Т.к.![]() ,
то
,
то
![]() где
где
![]()
Отсюда
![]()
![]() ,
а
,
а
![]()
Из формулы (1) при n=11 и h=1 получаем:
![]()
Т.к.
![]() (интерполируем не далее, чем на 1 шаг),
то
(интерполируем не далее, чем на 1 шаг),
то
![]()
![]()
Окончательно получаем:
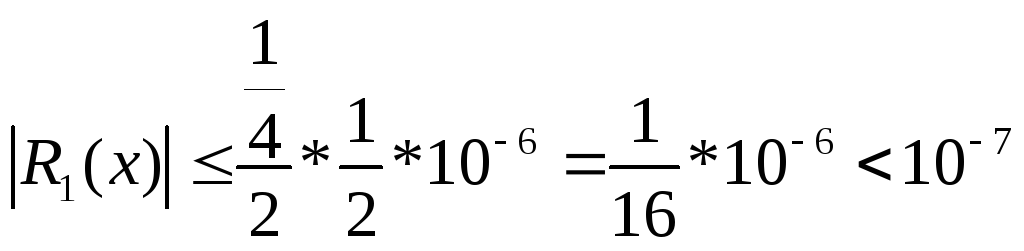
Т.о. погрешность интерполирования не превосходит погрешностей исходных данных!
Линейное интерполирование (h=1) возможно!!!
* * *
Интерполяционные формулы Ньютона
используют лишь значения функций,
лежащие лишь по одну сторону от выбранного
начального значения![]()
Для интерполирования в середине таблицы удобно применять формулы, содержащие как последующие, так и предшествующие значения функций по отношению к начальному ее значению. При этом используются центральные разности:
![]()
Причем:
![]()
![]()
![]()
Интерполяционные формулы с центральными разностями: формулы Гаусса, Стирлинга, Бесселя.
. Интерполяционная формула Лагранжа.
Для произвольно заданных узлов интерполирования (в том числе и для неравноотстоящих узлов ) применяется интерполяционная формула Лагранжа.
Н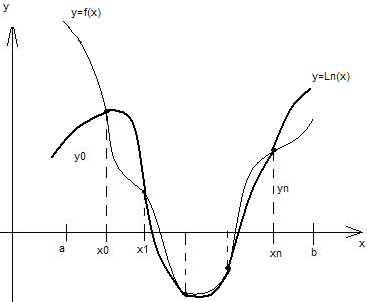 а
отрезке [a, b]
задано n+1 значений
аргумента и известны значения функций
y=f(x):
а
отрезке [a, b]
задано n+1 значений
аргумента и известны значения функций
y=f(x):
![]()
![]()
Требуется построить полином
![]() степени не выше n, имеющий
в заданных узлах
степени не выше n, имеющий
в заданных узлах
![]() ,
те же значения, что и функция f(x),
т.е. такой, что
,
те же значения, что и функция f(x),
т.е. такой, что
![]()
![]()
Рассмотрим частную задачу: построить
полином
![]() ,
такой, что бы
,
такой, что бы
![]() при
при
![]()
Т.е.
![]() (1)
(1)
Такой полином имеет вид:
![]() (2)
(2)
При
![]() - условие (1)
- условие (1)
Поэтому
![]()
И
![]()
В результате получаем:
![]() (3)
(3)
Будем теперь искать интерполяционный полином в виде
![]()
Этот полином имеет вид:
![]() (4)
(4)
Подставляя (3) в (4), получаем:
![]() (5)
(5)
----- интерполяционная формула Лагранжа
Можно доказать единственность полинома Лагранжа
При n=1 имеем:
![]()
![]()
![]() - уравнение прямой, проходящей через
две заданные точки: (
- уравнение прямой, проходящей через
две заданные точки: (![]()
При n=2 получаем уравнение параболы, проходящей через три точки:
![]()
(точки
![]()
Пример: Для функции
![]() построить интерполяционный полином
Лагранжа, выбрав узлы:
построить интерполяционный полином
Лагранжа, выбрав узлы:
![]()
Решение: Вычисляем
![]()
![]()
По формуле (5) получаем:
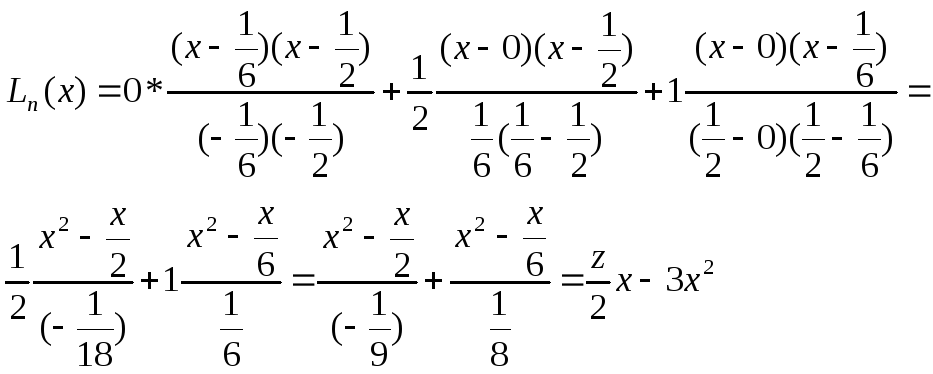
Точность не велика, т.к. синусоиду мы интерполируем параболой (квадратичной).
`Оценка погрешности интерполяционной формулы Лагранжа.
![]() (6)
(6)
где
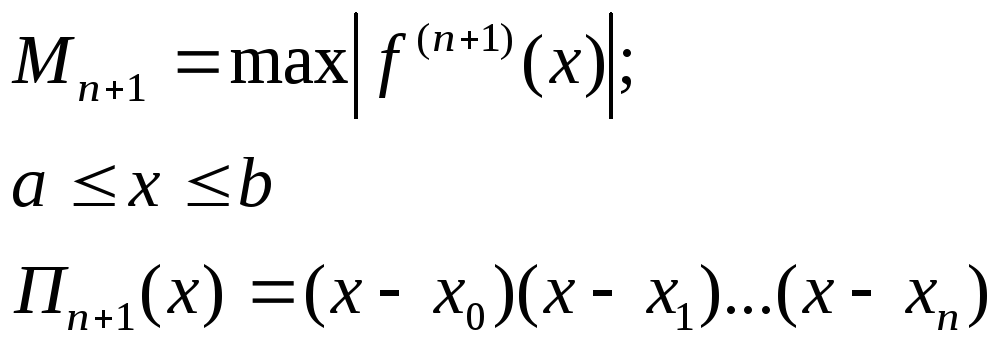
Пример1: с какой точностью можно
вычислить
![]() с помощью интерполяционной формулы
Лагранжа для функции
с помощью интерполяционной формулы
Лагранжа для функции
![]() ,
выбрав узлы интерполирования
,
выбрав узлы интерполирования
![]() Три точки n=2.
Три точки n=2.
Решение: имеем
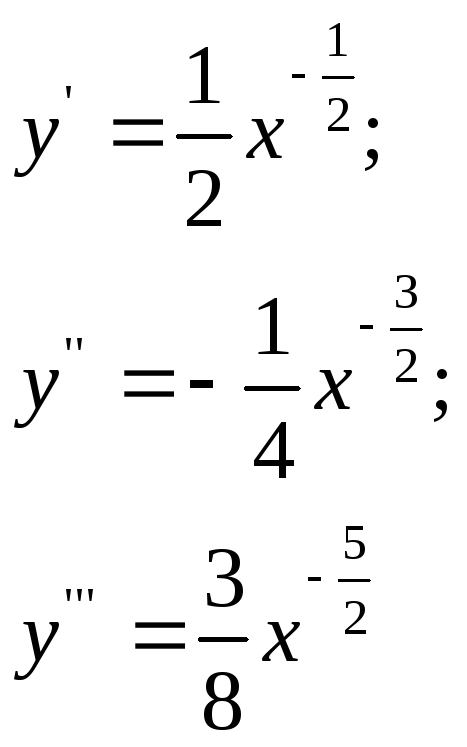 Отсюда
Отсюда
![]() (т.к.
(т.к.
![]()
Из формулы (6) получаем:
![]()
Пример2 с какой точностью можно
вычислить
![]()
![]() по формуле Лагранжа
по формуле Лагранжа
![]()
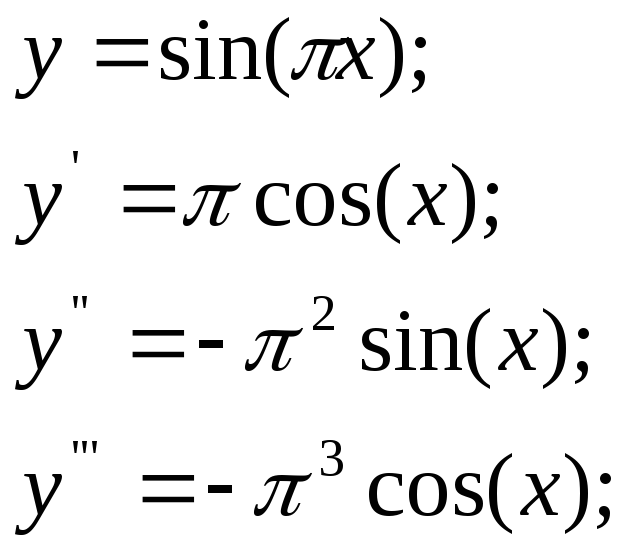
![]()
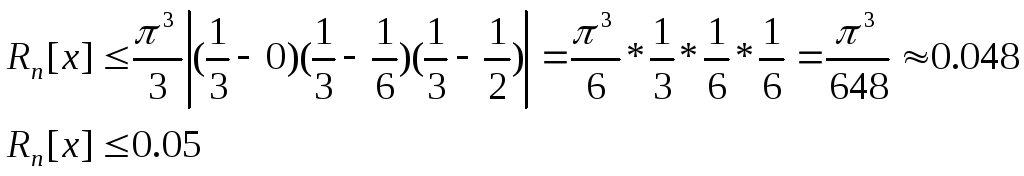
Точное значение
![]()
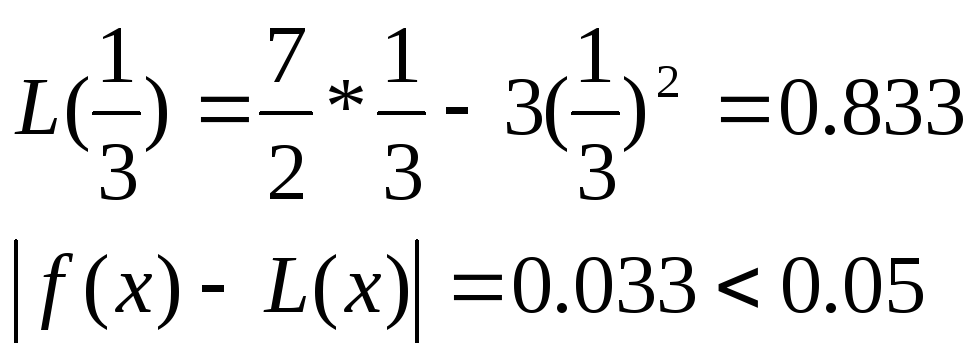
6 Обратное интерполирование
Задача обратного интерполирования: по
заданному значению функции
![]() найти аргумент
найти аргумент
![]() ,
при котором
,
при котором
![]() .
Функция y=f(x)
задана таблично.
.
Функция y=f(x)
задана таблично.
Предположим, что на отрезке [a,
b], содержащем узлы
интерполяции, функция f(x)
монотонна. Тогда существует
однозначная обратная функция x=F(y).
Она задана той же таблицей, что и y=f(x),
только теперь аргументом будет значение
![]() ,
а
,
а
![]() -соответствующее
значение функции.
-соответствующее
значение функции.
В этом случае обратное интерполирование
сводится к обычному интерполированию
для функции x=F(y).
Т.е. строится интерполяционный многочлен
( например, по формуле Лагранжа) –
многочлен
![]() .
При подстановке в
.
При подстановке в
![]() значения
значения
![]() - получаем
- получаем
![]() .
.
Второй способ применим ко всякой
функции f(x)
( не обязательно к монотонной!). Не
меняя ролями функцию и аргумент,
записываем по какой – либо формуле
интерполяционный многочлен
![]() .
Неизвестное значение
.
Неизвестное значение
![]() находим приближенно, решая уравнение
находим приближенно, решая уравнение
![]() .
Если число узлов велико, то этот способ
нахождения
.
Если число узлов велико, то этот способ
нахождения
![]() приводит к решению системы алгебраических
уравнений высокого порядка.
приводит к решению системы алгебраических
уравнений высокого порядка.
Рассмотрим другой - интерполяционный метод решения уравнений.
Будем рассматривать только равноотстоящие
узлы, т.е.
![]()
Пусть для определенности
![]() находится между
находится между
![]() и
и
![]() .
Строим интерполяционный многочлен по
1-ой формуле Ньютона. Уравнение
.
Строим интерполяционный многочлен по
1-ой формуле Ньютона. Уравнение
![]() принимает вид:
принимает вид:
![]() (2)
(2)
Выберем начальное приближение
![]()
Подставляя
![]() в (2) последовательно получаем
в (2) последовательно получаем
![]()
Итерационный процесс прекращается, когда два соседних приближения совпадают с заданной системой точности.
Т.о. находится
![]()
Т.к.
![]() то
то
![]()
Пример: функция y=f(x) задана таблично
|
х |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
у |
1,6487 |
1,8221 |
2,0138 |
2,2255 |
2,4596 |
Найти значение
![]() ,
для которого
,
для которого
![]() =1,7333
=1,7333
Решение: строим таблицу конечных разностей заданной функции.
|
х |
у |
|
|
|
|
|
0,5 0,6 0,7 0,8 0,9 |
1,6487 1,8221 2,0138 2,2255 2,4596 |
1734 1917 2117 2341 |
183 200 224 |
17 24
|
7 |
Т.к.
![]() т.е.
т.е.![]() ,
воспользуемся 1-ой интерполяционной
формулой Ньютона (2), подставив в нее
значения разностей из таблицы.
,
воспользуемся 1-ой интерполяционной
формулой Ньютона (2), подставив в нее
значения разностей из таблицы.
![]()
![]()
Получаем:
![]()
Т.к. решение ищем с точностью до 0,0001,
(4-ре значащих цифры после запятой), то
![]()
![]()
![]() - шаг по х.
- шаг по х.
ЛЕКЦИЯ 10
Сплайн – интерполяция.
(spline – рейка, планка)
Механические сплайны – гибкие деревянные
рейки, закрепленные на концах. В узлах
(точках) интерполяции подвешивают
грузила. Сплайн принимает форму,
минимизирующую его потенциальную
энергию. Если сплайн представить функцией
S(x) , то S
и
![]() непрерывны на [
непрерывны на [![]() ].
].
Кубическая сплайн – функция,
удовлетворяющая условиям
![]() называется естественным кубическим
сплайном. С математической точки зрения
кубическая сплайн – функция – единственная
функция, обладающая свойством минимальной
кривизны, среди всех функций, интерполирующих
данные точки и имеющих квадратичную
интегрируемую вторую производную.
называется естественным кубическим
сплайном. С математической точки зрения
кубическая сплайн – функция – единственная
функция, обладающая свойством минимальной
кривизны, среди всех функций, интерполирующих
данные точки и имеющих квадратичную
интегрируемую вторую производную.
Т.е. кубический сплайн есть самая гладкая из функций, интерполирующих заданные точки.
Пусть отрезок [a, b]
разбит на n частей точками
![]()
Сплайном k-ой степени
называется функция, представляющая
собой многочлен не выше к-ой степени на
каждом из последовательно примыкающих
друг к другу интервалов
![]()
![]() причем в точках стыка двух интервалов
причем в точках стыка двух интервалов
![]()
![]() функция непрерывна вместе со своими
производными до порядка не выше к
функция непрерывна вместе со своими
производными до порядка не выше к
![]() Сплайн
1-ой степени – кусочно-линейная функция
(непрерывная). Производная терпит разрыв
в точках излома.
Сплайн
1-ой степени – кусочно-линейная функция
(непрерывная). Производная терпит разрыв
в точках излома.
Задача интерполяции функции
![]() на
отрезке [a, b]
кубическим сплайном (сплайном 3-ей
степени) состоит в нахождении функции
S(x), равной
многочлену третьей степени
на
отрезке [a, b]
кубическим сплайном (сплайном 3-ей
степени) состоит в нахождении функции
S(x), равной
многочлену третьей степени
![]() на
каждом отрезке
на
каждом отрезке
![]() т.е.
т.е.
![]()
![]() (1)
(1)
Значения сплайна в узлах интерполяции
![]() равны
равны
![]() и сплайн-функция S(x)
непрерывна в узлах интерполяции вместе
с производными первого и второго
порядков.
и сплайн-функция S(x)
непрерывна в узлах интерполяции вместе
с производными первого и второго
порядков.
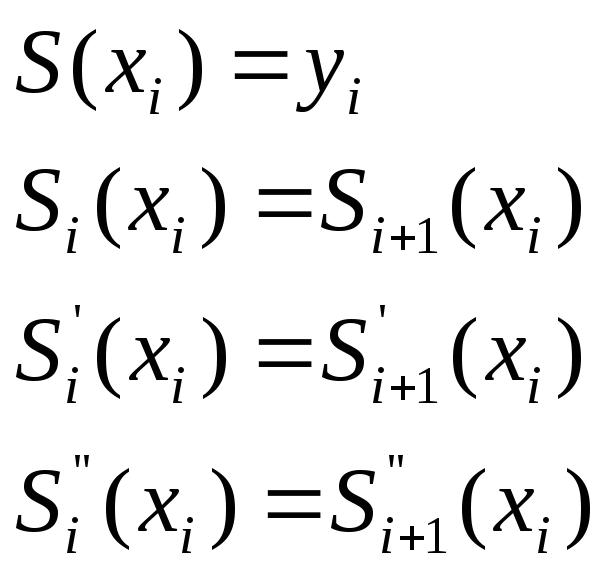
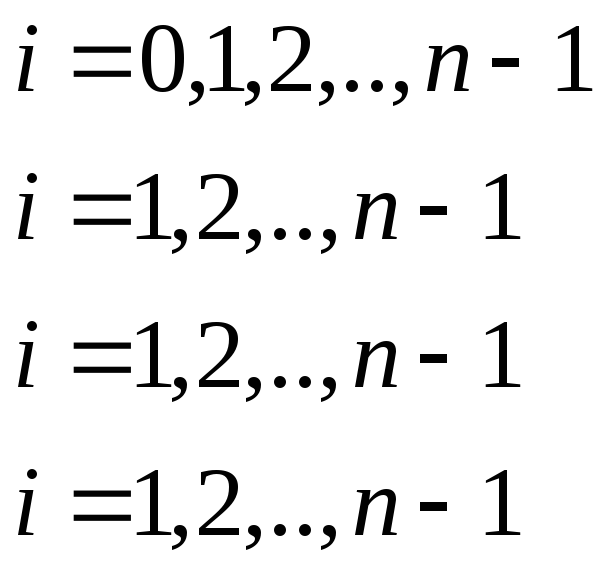
![]()
![]()
В сплайне (1) неизвестные
![]()
![]() .
Интервал [a, b]
разбит на n участков. Т.
о. имеем 4n неизвестных:
(i*p) = 4n.
.
Интервал [a, b]
разбит на n участков. Т.
о. имеем 4n неизвестных:
(i*p) = 4n.
Уравнения (2) – (5) дают 4n
– 2 уравнения. Т.о. для определения
величин
![]() необходимо ввести еще каких-либо 2
ограничения. В качестве ограничений
выбирается одна из 3-х пар краевых
условий:
необходимо ввести еще каких-либо 2
ограничения. В качестве ограничений
выбирается одна из 3-х пар краевых
условий:
![]()
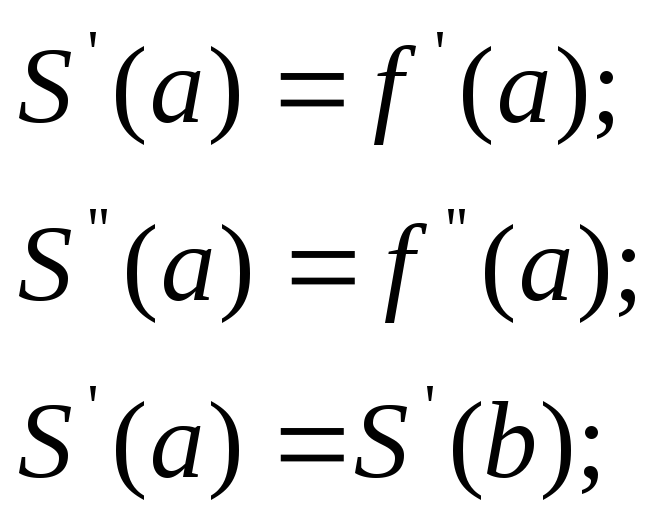
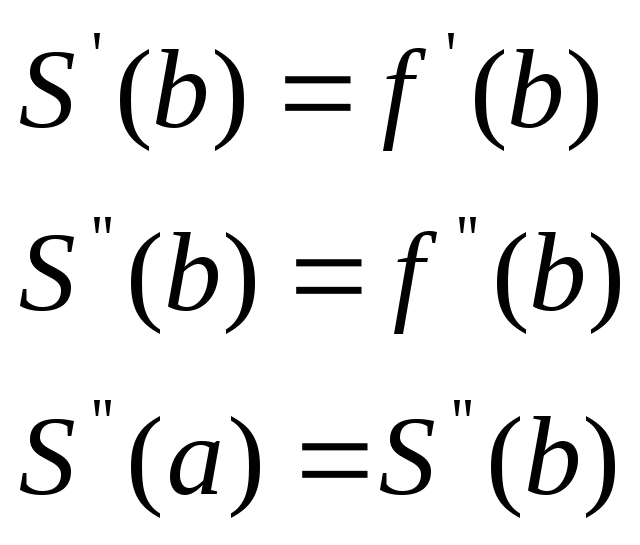
Построим сплайн, удовлетворяющий краевым условиям I типа.
Введем величины
![]() ,
называемые наклонами сплайна в узлах
,
называемые наклонами сплайна в узлах
![]() (i=0,1,..,n)
(i=0,1,..,n)
Интерполяционный кубический сплайн вида
![]() (6)
(6)
Где
![]()
![]() удовлетворяет условиям (2) – (4) для
любых
удовлетворяет условиям (2) – (4) для
любых
![]()
Из условия (5) и краевых условий (I)
можно определить параметры
![]() .
.
Действительно, легко проверить, подставляя
![]() в
(6) и т.д., что
в
(6) и т.д., что
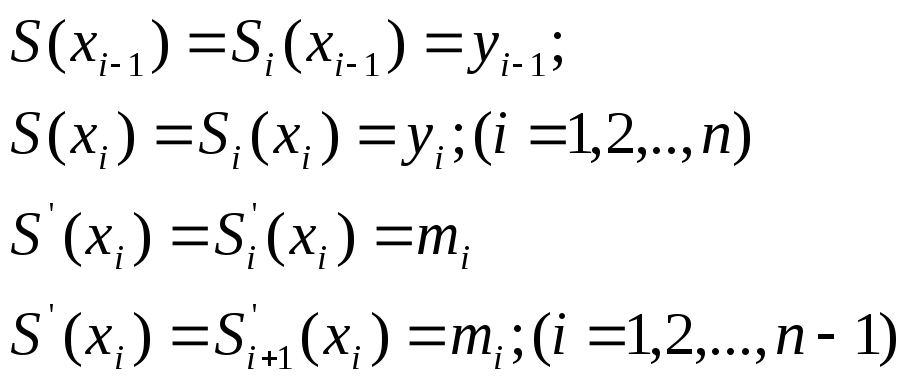
С учетом выражений : (беря вторые
производные от S(x)
по х и подставляя
![]() и
и
![]() )
)
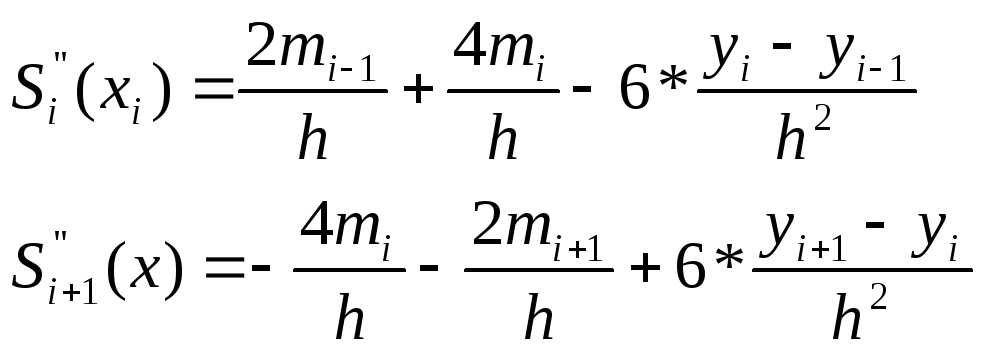
![]()
И краевых условий (I) и
условий (S) получим систему
из n+1 линейных уравнений
относительно неизвестных
![]()
(Приравнивая :
![]()
![]()
![]()
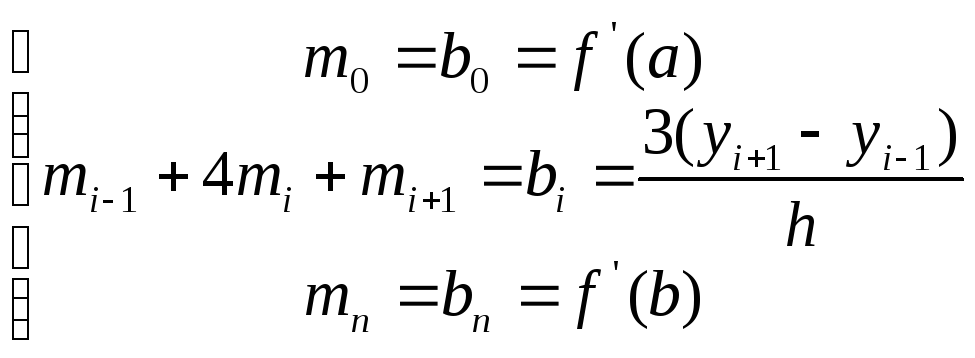
![]() (7)
(7)
Решая систему (7) методом Гаусса, получаем в результате прямой прогонки коэффициенты:
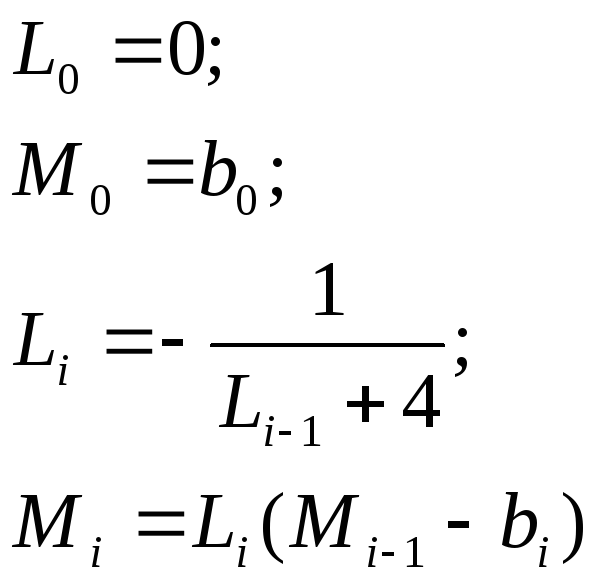
![]() (8)
(8)
Обратной прогонкой получаем результат:
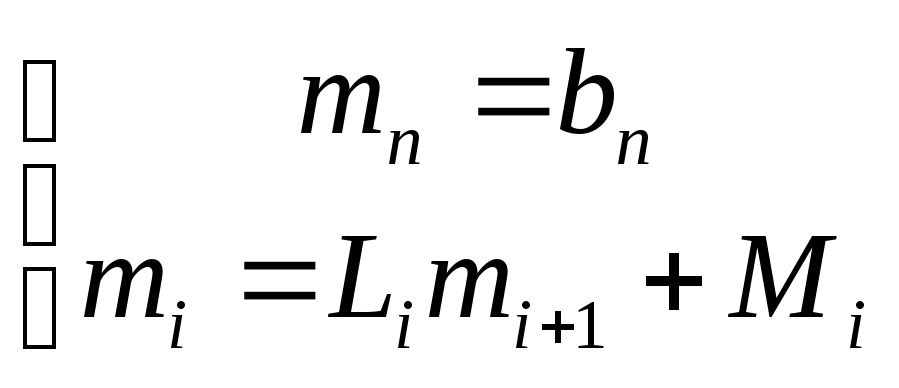
![]() (9)
(9)
Результаты (8) и (9) позволяют построить кубический сплайн (6)
Построение сплайна с учетом краевых условий (II) производится аналогично!
Точность интерполяционной функции f(x), имеющей на отрезке [a, b] непрерывные производные до 3-его порядка включительно, кубическим сплайном S(x) по точкам равномерного разбиения отрезка с шагом h при любых краевых условиях (I – III), оценивается неравенством:
![]() где
где
![]()
![]() (10)
(10)
! Неравенство (10) дает завышенную оценку точности.
Пример: На отрезке [0,
![]() ]
построить кубический сплайн с шагом
]
построить кубический сплайн с шагом
![]() ,
интерполирующий функцию
,
интерполирующий функцию
![]() ,
если заданы значения функции в трех
узлах интерполяции:
,
если заданы значения функции в трех
узлах интерполяции:
-
x
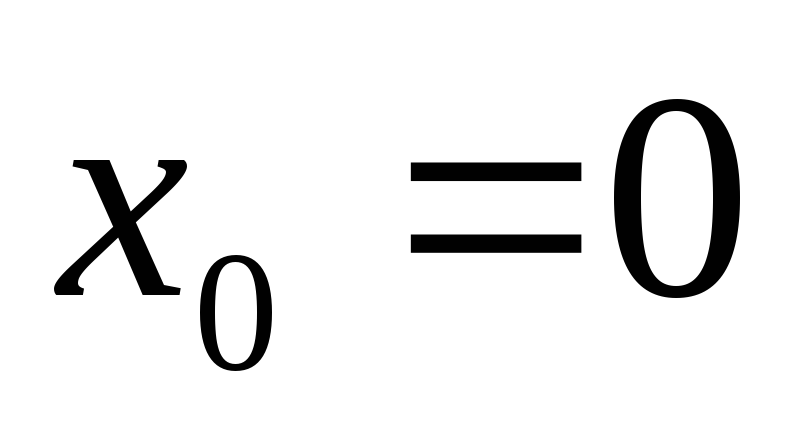
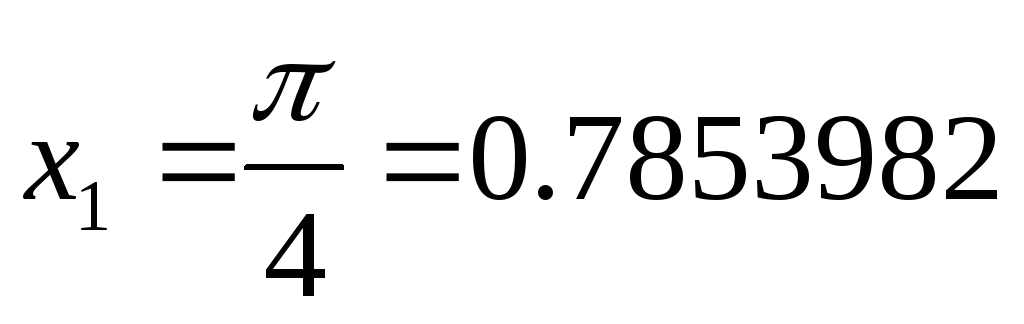
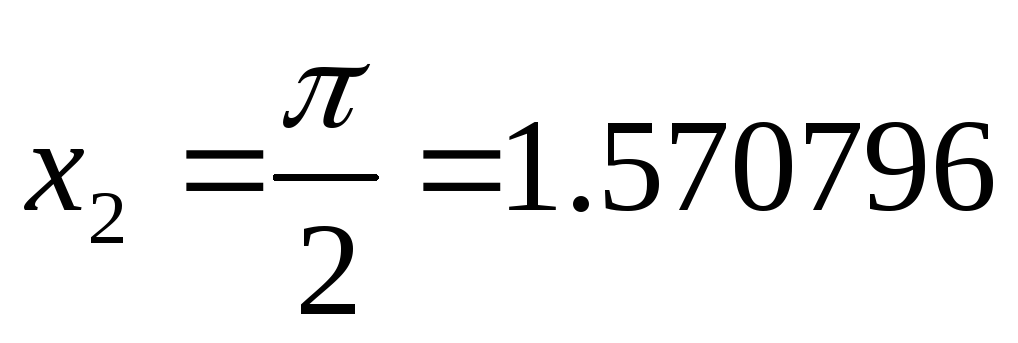
Sin(x)
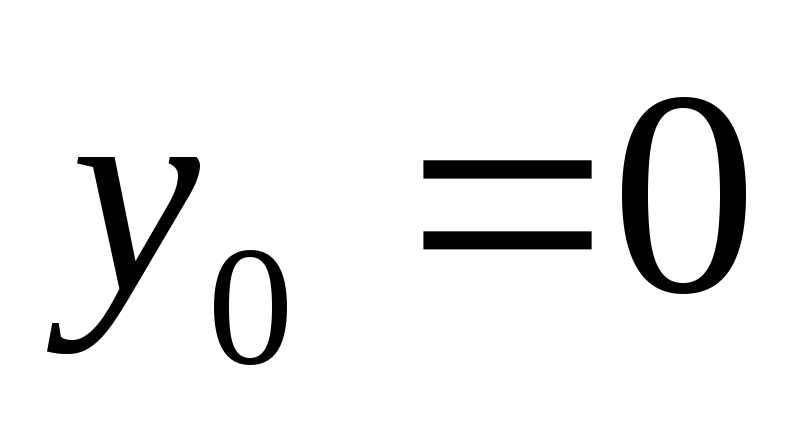
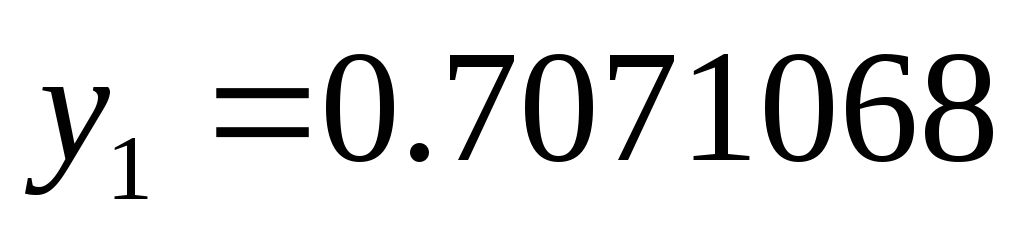
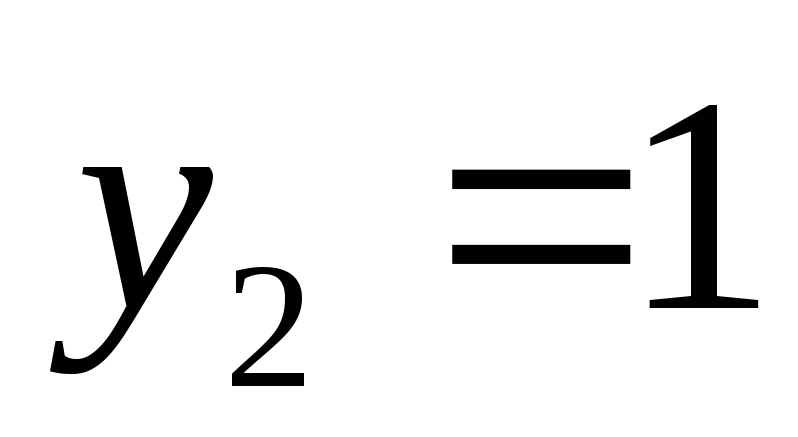
С помощью интерполяционной формулы
вычислить приближенное значение
![]()
![]() и сравнить с точным значением 0,5.
и сравнить с точным значением 0,5.
Решение: Т.к. задано 2 отрезка,![]() , то представим сплайн в виде:
, то представим сплайн в виде:

Краевые условия (I) имеют вид:
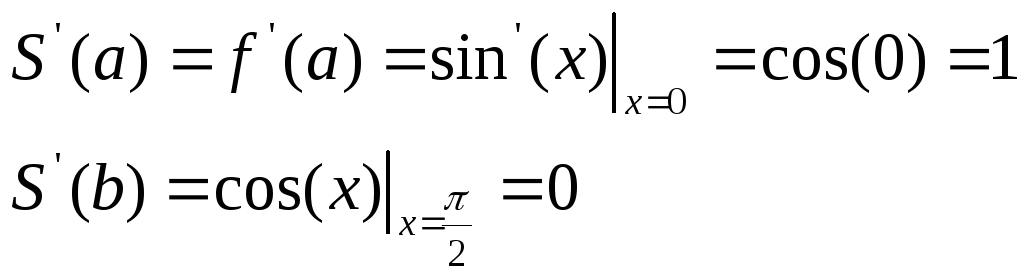
Из системы уравнений (7) имеем:
![]()
Находим
![]()
![]()
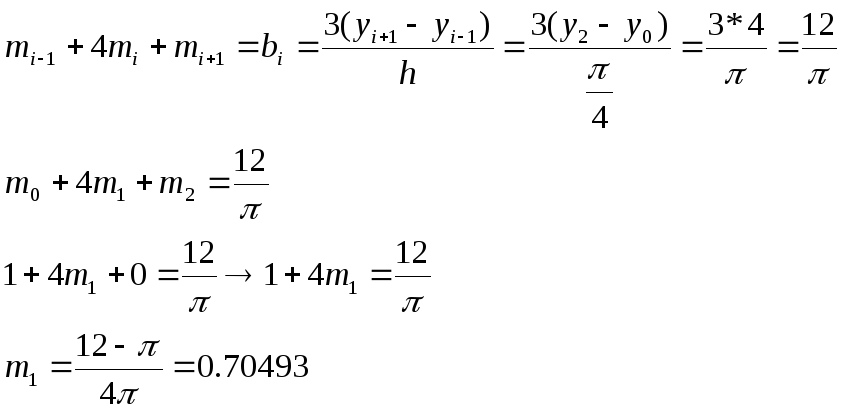
Подставляем значения
![]() в (6). Получаем:
в (6). Получаем:
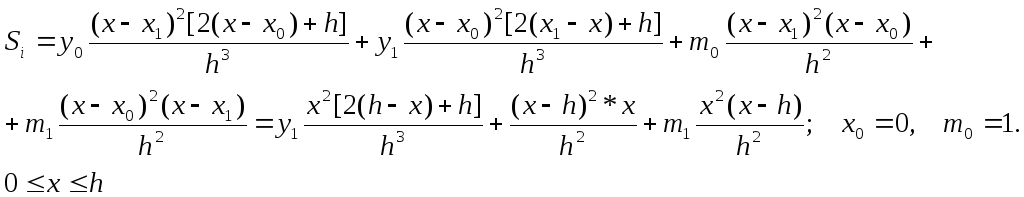
( т.к.
![]() и числа, содержащие
и числа, содержащие
![]()
Аналогично:
![]()
Получаем для
![]() :
(т.к.
:
(т.к.
![]()
![]()
Т. о.
![]()
Погрешность меньше
![]() !
!
Мы могли бы получить выражение для
![]() по формуле (8) и (9) – рекуррентные
соотношения, получаемые при прямом и
обратном прогоне в Методе Гаусса.
по формуле (8) и (9) – рекуррентные
соотношения, получаемые при прямом и
обратном прогоне в Методе Гаусса.
Действительно имеем:
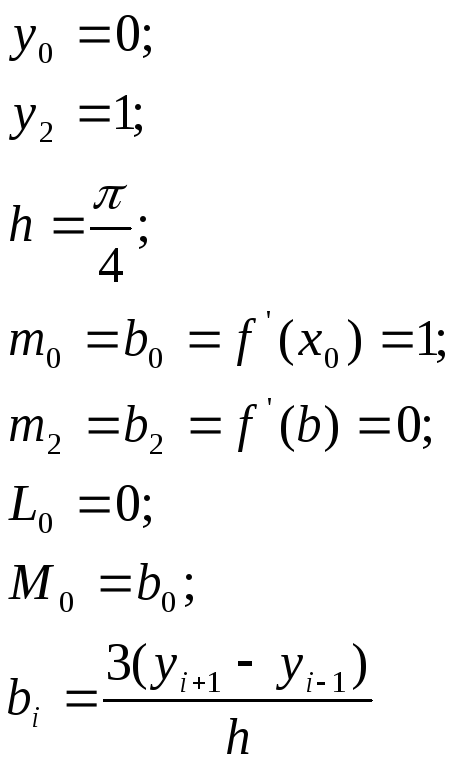 Находим:
Находим:
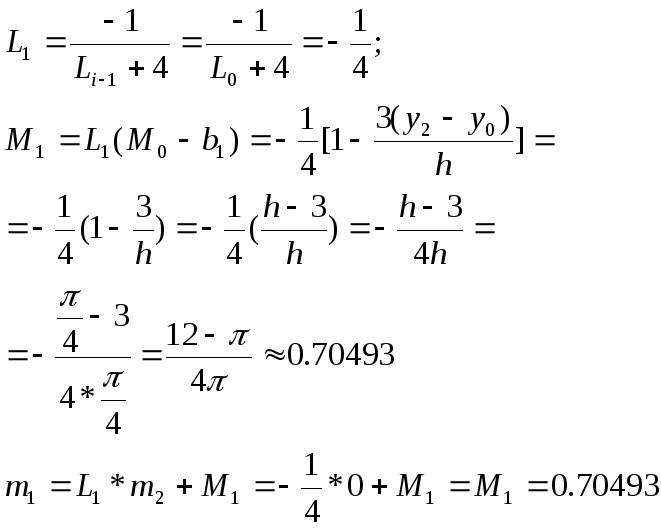
-
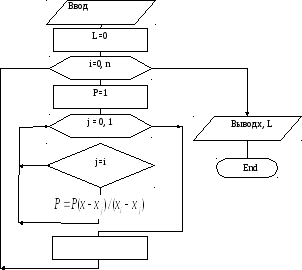
Блок – схема программ интерполяции
( Ракитин, Первушин «Практическое руководство по методам вычислений. 1998 )
=
![]()
