Закон Амдаля

Одной из целей при конструировании параллельных алго­ритмов является достижение по возможности большего ускорения; в идеальном случае . Однако мы уже видели на примере сложения n чисел, что эта ситуация не всегда достижима. В самом деле, максимальное ускорение можно получить только для задач, по существу тривиальных.

Главные факторы, обус­ловливающие отклонение от максимального ускорения, таковы:

1.     Отсутствие максимального параллелизма в алгоритме и/или несбалансированность нагрузки процессоров.

2.     Обмены, конфликты памяти и время синхронизации.

Хотя задержки, связанные с синхронизацией, обменами и конфликтами памяти, по своей природе весьма различны, их воздействие на общий процесс вычисления одинаково: они замедляют его на время, необходимое для подготовки данных, нужных для дальнейшего счета. Поэтому иногда следует объединять все три фактора задержки, как это сделано в сле­дующем определении.

Определение 7. Временем подготовки данных называется задержка, вызванная обменами, конфликтами памяти или синхронизацией и необходимая для того, чтобы разместить данные, требующиеся для продолжения вычислений, в соответствующих ячейках памяти.

Обратимся теперь к фактору отсутствия максимального параллелизма. Он может проявляться по-разному. При сложении n чисел мы видели, что на первом этапе алгоритма параллелизм максимален, однако на каждом последующем этапе степень параллелизма уменьшается вдвое. Таким образом, в большинстве случаев средняя степень параллелизма алгоритма меньше .

Рассмотрим теперь формальную модель ускорения, в которой

,

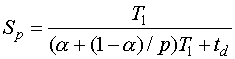где - время, затрачиваемое на реализацию алгоритма на одном процессоре, - доля операций в алгоритме, выполняемых одним процессором, - доля операций, выполняемых всеми процессорами, - общее время, требуемое для подготовки данных.

В случае если =0 и =0, ускорение максимально . Предпосылки данного случая заключаются в том, что все операции выполняются с максимальным параллелизмом и отсутствуют задержки на подготовку данных.

В случае =0 получаем формулу, выражающую закон Амдаля

.

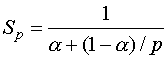Предположим, что , то есть половина операций в алгоритме может выполняться параллельно, а половина нет. Тогда ускорение принимает вид

.

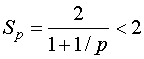Таким образом, независимо от количества процессоров и даже при игнорировании всех затрат на подготовку данных ускорение параллельного алгоритма всегда меньше 2.

25

Граф алгоритма — ориентированный граф, состоящий из вершин, соответствующих операциям алгоритма, и направленных дуг, соответствующих передаче данных (результаты одних операций передаются в качестве аргументов другим операциям) между ними. Не следует путать его с графом управления программы и тем более с её блок-схемой.

Активно используется при исследованиях скрытого параллелизма в алгоритмах, записанных на традиционных языках программирования последовательного типа.

Особенностями графа алгоритма являются:

• его ацикличность;

• невозможность, в общем случае, его описания простым перечислением, в силу того, что его составляющие могут зависеть от внешних параметров решаемой им задачи (например, алгоритм, реализующий метод Гаусса — от размера матрицы).

В ряде случаев (см., например, линейный класс программ) удаётся избавиться от излишнего лексикографического порядка и получить из текста программы, например, на Фортране, граф алгоритма, используя чисто формальную методику, которая может быть реализована в программных системах. После этого можно использовать его для подготовки параллельной реализации этого алгоритма, исследуя его характеристики, такие как развёртки или ярусно-параллельные формы. Эта методология распараллеливания развита с начала 80-х гг. XX века и описана в работах В. В. Воеводина и коллектива его последователей. На ее основе разработаны некоторые системы исследования параллельных структур в программах, наиболее известной из них является V-Ray, разработанная в НИВЦ МГУ.