3.4 Методы имитации на эвм случайных элементов

На функционирование реальных сложных систем - вычислительных систем (ВС), производственных участков, автоматизированных телефонных станций (АТС), систем передачи информации (СПИ) и т.д. оказывают влияние случайные факторы, которые в математическом моделировании сложных систем рассматриваются либо как случайные входные (управляющие) сигналы и, либо как неконтролируемые воздействия внешней среды v.

Примерами таких случайных факторов являются: случайные интервалы времени между поступлениями заданий в ВС, деталей на производственный участок, вызовов в АТС, обращений к СПИ, а также время выполнения заданий в ВС, обработки деталей, установления связей и длительности переговоров в АТС, время обработки и передачи информации в СПИ и т.д.

При построении ИМ сложной системы S возникает необходимость в имитации случайных факторов по заданным законам распределения вероятностей. Так, в примере из раздела 3.3.1 при построении ИМ вычислительной системы возникла необходимость в имитации случайных интервалов между поступлениями заданий пользователя в систему и интервалов выполнения заданий процессором, т.е. задача имитации случайных величин по заданному вероятностному закону распределения. Объектом имитации могут быть не только случайные величины, но и случайные события, векторы, процессы, поля, множества, т.е. произвольные случайные элементы.

Раздел 3.4. Посвящен именно этим актуальным задачам имитации случайных элементов.

3.4.1 Принципы моделирования случайных элементов

Моделирование на ЭВМ случайного элемента подчиняется двум основным принципам:

1. сходство между случайным элементом-оригиналом и его моделью состоит в совпадении (близости) вероятностных законов распределения или числовых характеристик;

2. всякий случайный элемент определяется («конструируется») как некоторая борелевская функция от простейших случайных элементов, так называемых, базовых величин (БСВ).

Простейшим для моделирования на ЭВМ случайным экспериментом является эксперимент, заключающийся в бросании точки наудачу в промежуток [0, 1). Результатом этого эксперимента является координата точки. Математической моделью такого эксперимента является вероятностное пространство , где - пространство элементарных событий (элементарное событие заключается в том, что координата брошенной точки равна ); F - -алгебра, порожденная интервалами из ; P - вероятностная мера, определенная для событий (подмножеств) и совпадающая с мерой Лебега, так что для события :

(3.11)

Базовой случайной величиной (БСВ) на будем называть непрерывную СВ

(3.12)

Равномерно распределенную на полуинтервале [0, 1).

Функция распределенная БСВ имеет вид

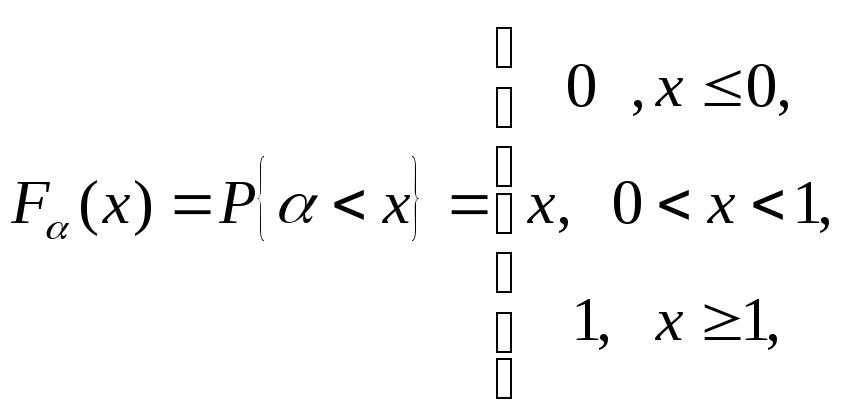(3.13)

а плотность распределения определяется формулой

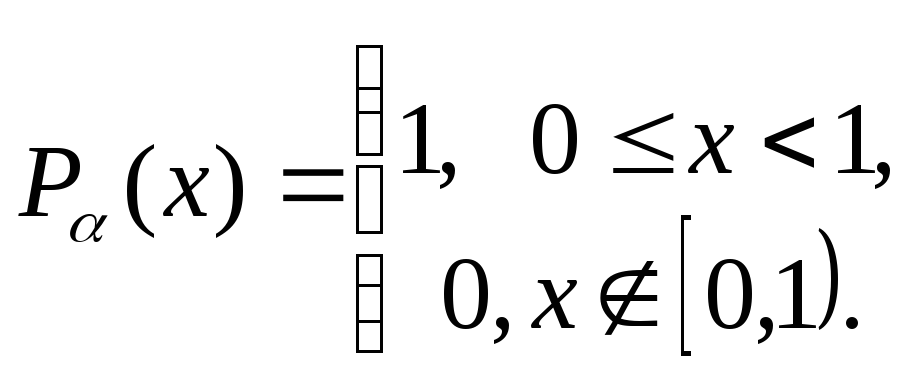
Будем обозначать закон распределения

Математическое ожидание БСВ (первый начальный момент)

дисперсия (второй центральный момент)

Наряду с простейшим экспериментом будем рассматривать составной случайный эксперимент, получающийся в результате r-кратного (r1) повторения независимо друг от друга простейших экспериментов. Результатом составного случайного эксперимента является последовательность из r независимых БСВ таких, что

где - координата точки, брошенной наудачу в [0, 1) в i -м простейшем эксперименте.

Совместная плотность распределения вероятностей .

Согласно второму принципу моделирования случайных элементов, любой случайный элемент представляется для некоторого натурального r в виде функции f(.) от r независимых БСВ

Таким образом, задача моделирования произвольного случайного элемента * разбивается на две подзадачи:

1) моделирование на ЭВМ независимых БСВ ;

2) нахождение функции f(.) такой, чтобы случайный элемент обладал требуемыми вероятностным законом распределения и числовыми характеристиками.

Поэтому моделирующий алгоритм состоит из двух блоков (рис. 3.13)

Б1 — блок моделирования БСВ (общий для всех );

Б 1

Б2

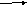
Рис.3.13 Моделирующий алгоритм БСВ

Б2 - блок функционального преобразования f(.) БСВ (различный для различных законов распределения вероятностей).

Для имитации одного и того же случайного элемента* может быть предложено несколько вариантов функциональных преобразований (способы построения f(.) будут описаны ниже). Обычно предпочтение отдается варианту f(.), требующему меньших вычислительных затрат; для этого используется понятие коэффициента использования БСВ.

Коэффициентом использования БСВ назовем величину, обратную числу r базовых случайных величин, используемых для моделирования одной реализации случайного элемента *:

Величина является мерой вычислительных затрат на моделирование *. Чем меньше , тем больше затраты. Целесообразно выбирать такую функцию f(.), для которой принимает наибольшее значение.

Очевидно, чтобы моделировать на ЭВМ случайные элементы с заданным вероятностным законом распределения, необходимо уметь моделировать БСВ. БСВ является абсолютно непрерывной случайной величиной (СВ). Однако на ЭВМ приходится иметь дело с дискретными случайными величинами. Поэтому моделирование БСВ основано на аппроксимации непрерывной СВ дискретной случайной величиной (ДСВ) . Опишем способ построения ДСВ .

Рассмотрим случай, когда представление целых неотрицательных чисел на ЭВМ осуществляется с помощью k двоичных разрядов (битов). Тогда С = {О, 1, 2^k - 1} — множество 2^k неотрицательных целых чисел, представимых в ЭВМ. Определим на (Q, , Р) дискретную случайную величину следующим образом:

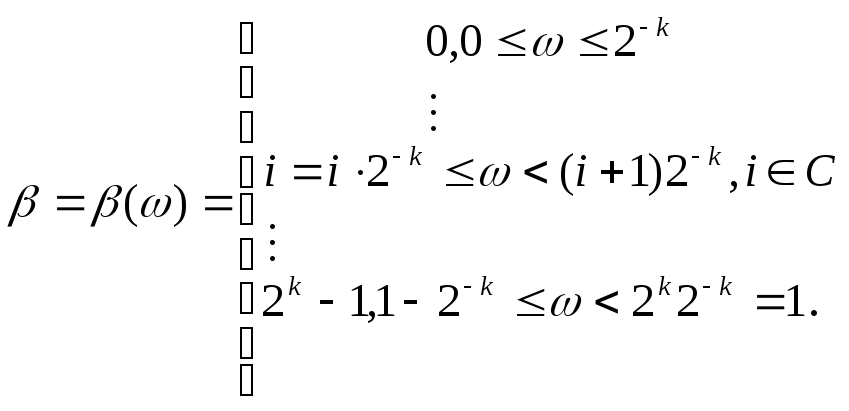(3.14)

Построение проиллюстрируем с помощью рис.3.14. Разобьем промежуток [О, 1) на 2^k отрезков одинаковой длины 2^-k; для , попадающих в промежуток полагаем С.

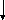
0 2^-k 22^-k…i2^-k (i+1) 2^-k…1-2^-k 1

Рис.3.14 Построение

По построению распределение дискретной СВ является равномерным на множестве С, то есть все значения равновероятны, действительно:

(3.15)

Теперь перейдем от СВ к искомой ДСВ :

(3.16)

Согласно (3.15)

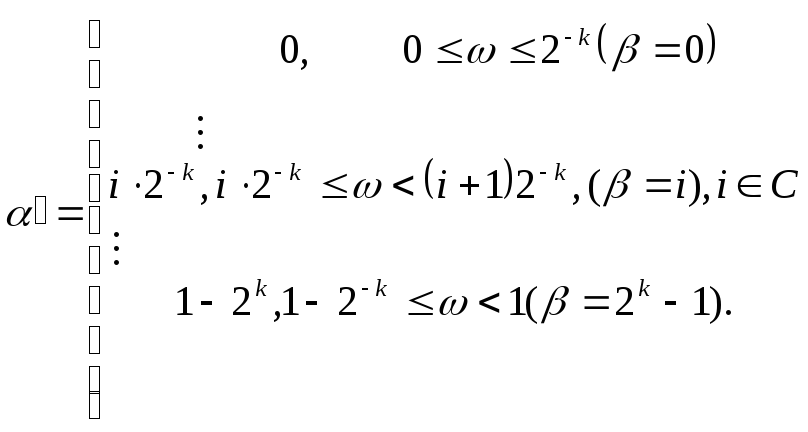
т.е. от целочисленной ДСВ мы перешли к ДСВ со значениями в [О, 1).

Очевидно, все возможные значения определяются множеством С' = {0, 2^-k,…,1-2^-k} и являются равновероятными:

,

т.е. закон распределения является равномерным на .

Точность аппроксимации с помощью устанавливается с помощью леммы.

Лемма. Для СВ и , определенных на и имеющих вид (3.12), (3.13) соответственно, равномерное уклонение удовлетворяет выражению.

(3.17)

Доказательство. Разобьем на 2^k промежутков согласно рис.3.14. Пусть . Тогда согласно (3.12) справедливо представление

а согласно 3.16

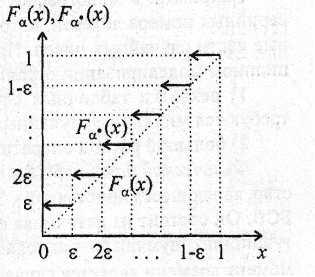
Рис.3.15 Функция распределения

Поэтому

Отсюда заключаем справедливость (4.34).

Из (3.17) следует, что если , то последовательность равномерно по . Таким образом, случайная величина является аппроксимацией для БСВ¹ ; называется в связи с этим квазиравномерной случайной величиной. Ее функция распределения изображена на рис.3.15 и аппроксимирует с точностью . Между математическими ожиданиями величин справедливо соотношение

В табл.3.4 приведены соотношения между дисперсиями величин и .

Таблица 3.4

k	2	3	5	10	15
	1,290	1,140	1,030	1,001	1,00

При достаточно больших значениях k (например, для ПЭВМ IBM PC AT 286

k =15, ; для ПЭВМ IBM PC AT 386, 486, 586 (Pentium) k = 31, величины отождествляют.