3.2 Математические модели

3.2.1 Понятие математической модели

Построение математической модели на этапе Э1 включает в себя пять взаимосвязанных подэтапов :

1. Уяснение и постановка задачи, определение целей исследования.

2. Декомпозиция системы на компоненты, допускающие удобное математическое или алгоритмическое описание.

3. Определение параметров, переменных, пространства состояний системы, установление пределов изменения каждой характеристики.

4. Выбор показателей КЦФ, т.е. вектора .

5. Описание концептуальной модели S` системы S по одному из представленных ниже типов и проверка ее адекватности.

В качестве примеров рассмотрим:

А) гибкую производственную систему обработки несущих конструкций РЭС (рис. 3.3), состоящей из автоматизированного склада, крана- штабелера, пунктов контроля, робота, накопителей и станков с ЧПУ.

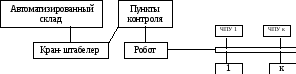
Рис. 3.3 ГПС обработки несущих конструкций РЭС

Б) Локальную сеть сбора, обработки и выдачи сигналов управления для разнесенных пространственных объектов (рис.3.4), состоящую из А_n преобразователей и В_n микропроцессорных модулей приемо-передатчиков, выдающих с заданным периодом по радиоканалу информацию о текущих значениях параметров и с высшим приоритетом аварийные сигналы. Центральный приемо-передающий модуль-концентратор (ЦППК), центральный процессор (ЦП), способный вырабатывать и передавать на преобразователи новые уставки и сигналы управления

А₁

В₁

связь по радиоканалу

ЦППК

ЦП

А_N

В_N

команды управления

Рис. 3.4 Локальная информационно-управляющая сеть

Введем обозначения: - временной интервал моделирования системы S (интервал модельного времени), где:

• t₀ время начала моделирования (обычно полагают t₀ = 0);

• Т – время окончания моделирования;

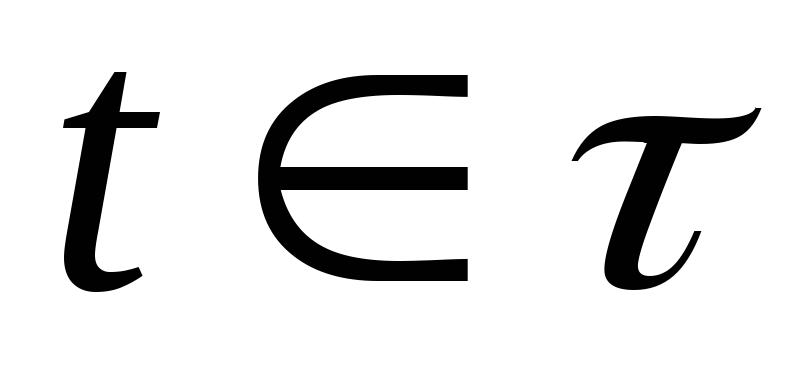• - текущее значение модельного времени.

Построение математической модели системы S начинается с определения параметров системы и переменных, определяющих процесс функционирования системы.

Физическую интерпретацию вводимых здесь понятий будем давать, используя пример ГПС (рис.3.3).

Параметры системы - это характеристики системы, остающиеся постоянными на всем интервале моделирования .

Если значения определены на некотором множестве , т.е.

,

то говорят, что имеется параметрическое семейство систем.

Пример. Количество единиц оборудования и технические характеристики оборудования в ГПС.

Множество переменных разбивают на два подмножества – независимых и зависимых переменных.

1. К независимым переменным отнесем следующие характеристики.

• Входные воздействия на систему (сигналы): u₁, u₂,…,u_n1. Входные воздействия в момент t Т характеризуются вектором

u = u(t) = (u₁(t),…,u_n1(t)) URⁿ¹.

Среди {u_i} могут быть управляющие воздействия, например, u₁, u₂,…, а остальные n₁-n_1' воздействий - неуправляющие.

Пример входных воздействий - управляющие воздействия, поступающие с ЦПУ на управляемые компоненты ГПС.

• Воздействия внешней среды: Среди них могут быть контролируемые (наблюдаемые) и неконтролируемые (ненаблюдаемые), детерминированные и случайные воздействия. В момент t Т они характеризуются вектором

v= v(t) = (v₁(t),…,v_n2(t))V Rⁿ².

Пример. Наличие дефектов у заготовок: внешние дефекты - контролируемые, а внутренние (скрытые) - неконтролируемые воздействия; случайные интервалы времени между поступлением деталей на обработку.

• Переменные, характеризующие состояние системы , x₁, x₂,…,x_n3. В отличие от {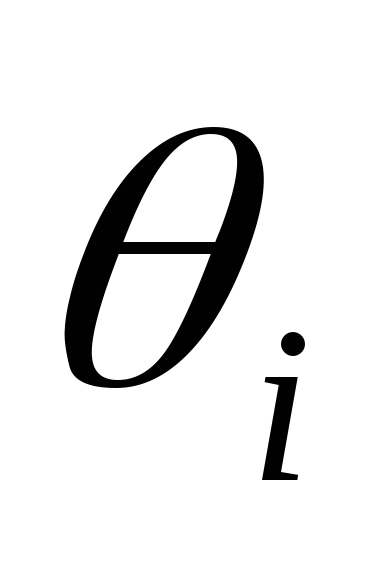} состояния {x_i} характеризуют свойства системы, изменяющиеся во времени. Состояние системы в момент 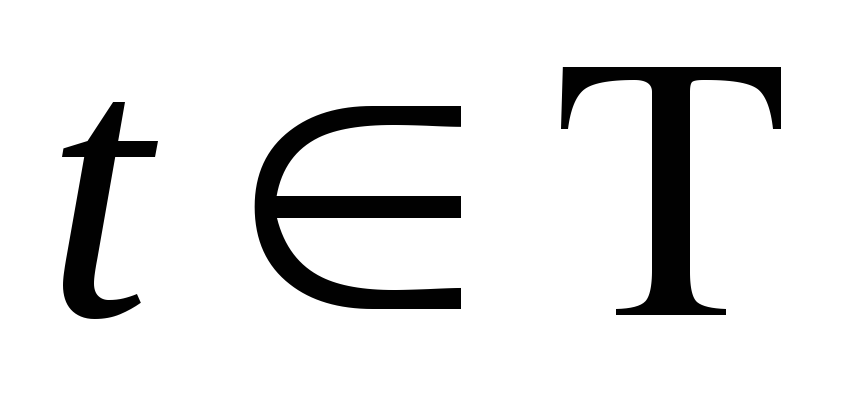описывается вектором

x= x(t) = (x₁(t),…,x_n3(t))XRⁿ³

где X - пространство состояний или фазовое пространство системы (множество возможных значений вектора х). Если t₁< t₂ <… - моменты изменения cостояния системы, то последовательность x(t₁), x(t₂),… называется фазовой траекторией системы.

Пример. x(t) = (x₁, x₂) - вектор, описывающий состояние обрабатывающих центров ГПС в момент ,

x_i=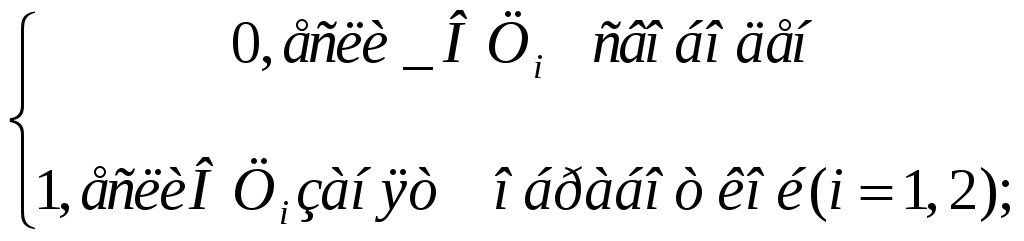

X = {(0,0), (0,1), (1,0), (1,1)}

2. К зависимым переменным отнесем следующие характеристики.

• Выходные характеристики (сигналы) системы у₁, у₂, ...,у_n1 определяемые в момент 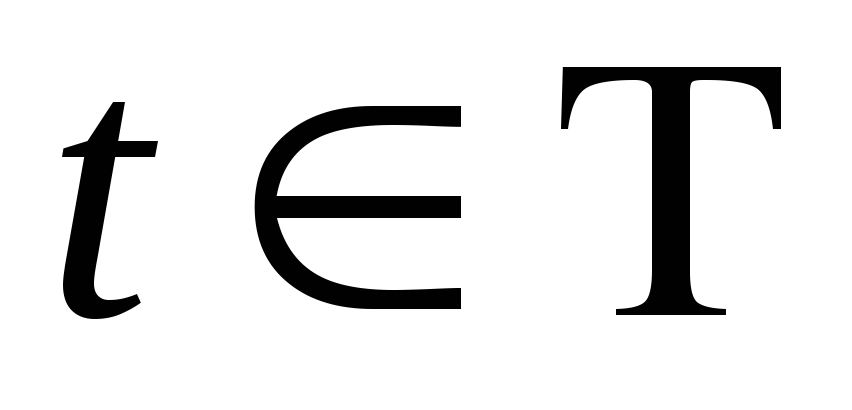вектором

y = y(t)= (y₁(t),…y_n4(t)).

Пример. Сигналы, поступающие из ОЦ₁ и ОЦ₂ на ЦПУ, являются выходными для обрабатывающих центров и управляющими для ЦПУ.

• Показатели КЦФ системы q₁, q₂,…q_k характеризуют ее цели, (т.е. характеризуют достижения системой функционирования системы) и образуют вектор

q = q(t) = (q₁(t),…,q_k(t))QR^k, t

Пример. Производительность ГПС за смену, расход материальных ресурсов.

При наличии в системе случайных факторов (например, случайных воздействий внешней среды) значения являются также случайными и поэтому не могут служить показателями КЦФ. В этих случаях в качестве Q используют средние значения {Q_i} , определяемые соотношениями

где E{.} - символ математического ожидания (см. раздел 2.3).

• Внутренние параметры СУ 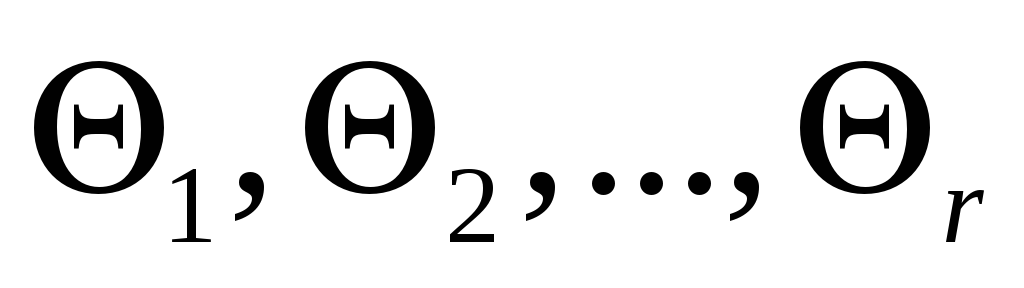, практически не зависящие от времени и могущие изменяться только по желанию исследователя.

Связи между зависимыми и независимыми переменными изображены на рис. 3.5.

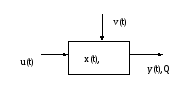
Рис. 3.5. Связь между переменными

Процесс функционирования системы во времени описывается операторными соотношениями (заданными аналитически или алгоритмически) для состояний, выходных характеристик КЦФ системы:

(3.1)

где обозначают реализацию процесса u(t) на отрезке [0,t], аналогично обозначены x^(t), y^(t) .

Через обозначены соответствующие операторы, описывающие динамику зависимых и независимых переменных и показателей эффективности.

Зависимости (3.1) называются законами функционирования системы S; зависимость y = y(t), t называется выходной траекторией системы, в зависимость x = x(t), t - фазовой траекторией.

В выборе переменных x(t) , характеризующих состояние системы в момент времени tT , обычно имеется произвол, который используется так, чтобы упростить закон функционирования (4.1) и привести его к виду

x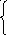(t) = F(x⁽⁰⁾, u^(t), v^(t), , t),

y(t) = G₁(x^(t), t), (3.2)

q(t) = G₂ (x^(t), t), t

где - некоторые операторы; x⁽⁰⁾ - начальное состояние системы. Закон (3.2) отличается от (3.1) следующими особенностями:

1. состояние системы S в момент времени tзависит от начального состояния системы x⁽⁰⁾;

2. выходные характеристики и показатели эффективности системы в момент времени t зависят от состояний x^(t) и текущего времени.

Пример. Для ГПС, состоящей из двух обрабатывающих центров, влияние воздействия внешней среды, состоящее в наличии отклонений параметров заготовок от стандартов, учтем при формировании фазового пространства, Пусть x_i(t), i = 1,2 - переменная, характеризующая состояние i-го ЧПУ в момент времени t. Положим:

,

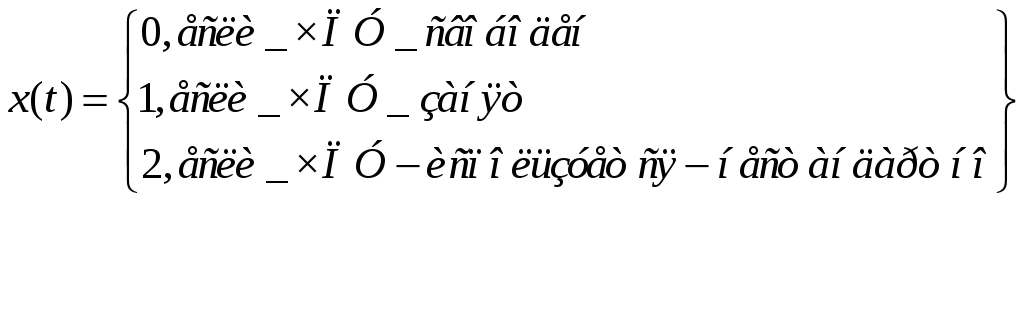
Тогда влияние на y(t), w(t) воздействия внешней среды v(t) будет учтено в состоянии системы x(t) .

Математической моделью системы называют множество переменных u, v, θ, y, q вместе с законом функционирования в виде (3.1) или (3.2).

Опишем теперь классификацию математических моделей. Операторные соотношения в (3.1), (3.2) могут быть заданы аналитически, то есть с помощью функциональных соотношений или логических условий, либо алгоритмически. В зависимости от способа задания закона функционирования математические модели делятся на аналитические и алгоритмические.

Отметим, что время t может рассматриваться и как непрерывная переменная: t Т = [0,T], и как дискретная.

t = i, i = 0,1,...,M, М = [Т/],

где - шаг дискретизации. При этом, соответственно, имеем непрерывные (H) и дискретные (Д) математические модели. Если математическая модель не содержит случайных элементов, то имеем детерминированную модель (Дт); в противном случае имеем вероятностную (В) модель. Таким образом, по признакам непрерывности и стохастичности можно выделить четыре обширных класса математических моделей: непрерывно-детерминированные (НДт) модели; дискретно-детерминированные (ДДт) модели; дискретно-вероятностные (ДВ) модели; непрерывно-вероятностные (НВ) модели. Элемент классификации аналитических моделей приведен в таблице 3.1

Таблица 3.1 Классификация математических моделей

Тип ММ Харак- теристика	НДт	ДДт	ДВ	НВ
Вид зависимости	Дифференциальные и интегральные уравнения	Теория разностных уравнений, конечные автоматы	Разностные стохастические уравнения, вероятностный автомат	Стохастические дифференциальные уравнения, теория массового обслуживания

Примечание: Представленная таблица не претендует на полноту, является лишь иллюстрацией предлагаемой классификации. Остальные модели можно посмотреть в монографии автора, в данном учебном пособии представлены только непрерывно-вероятностные модели, представляющие интерес для имитационного моделирования, один из представителей НВ моделей – теория массового обслуживания выделена в таблице.