Глава 3. Моделирование – инструмент исследования и проектирования систем

3.1 Классификация моделей

Из предыдущих глав очевидно, что процессы исследования СУ невозможно качественно осуществить без использования методов математического и/или компьютерного моделирования. Первоначально под моделью понималось вспомогательное средство, заменяющее исследуемый объект (модель плотины, машины, манекен), затем модель стала восприниматься не только как способ существования знаний, но и как активный этап процесса создания систем, заменяя собой в ряде случаев этапы проектирования. Любой алгоритм – это модель деятельности и в силу системности мира моделей – любая целесообразная деятельность невозможна без моделирования. Естественно, что модель не заменяет оригинала, а является его целевым отображением. Классификация мира моделей весьма широка, поэтому отметим две градации моделей:

1. Познавательные модели, являющиеся формой организации и представления знаний (таблица Менделеева, модель атома Бора), часто подгоняемые под реальность.

2. Прагматические модели, являющиеся средством управления и организации практических действий (ГОСТ, КТД, план, устав, кодекс) и пытающиеся реальность приблизить к модели.

На рис.3.1 приведена классификация, применимая в первую очередь для задач, очерченных пособием

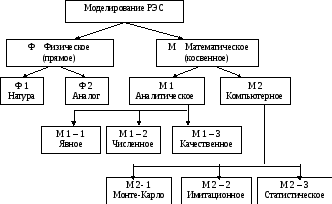
Рис. 3.1 Классификация методов моделирования

Физическое моделирование предусматривает, что в качестве модели используется либо сама система Ф1 (опытный образец), либо другая система Ф2 со схожей физической природой. Такой вид моделирования способствовал созданию теории подобия.

Математическое моделирование состоит из двух больших групп М1 и М2, включающих в себя: М1–1 – явное аналитическое моделирование, когда стремятся получить в общем виде явные аналитические зависимости для искомых характеристик, М1-2 использующие приближенные численные методы, когда все объекты аппроксимируются числами или их комплектами, М1-3 – качественные методы, когда изучаются свойства решений задач данного класса без нахождения самих решений. Такого вида методы широко применяются в теории квалиметрии, в экономике, социологии и т.д.

Для компьютерного проектирования М2 характерно, что математическая модель системы представляет собой программу для ЭВМ, т.е. компьютерную модель, с которой можно проводить вычислительные эксперименты (ВЭ). Характерно, что с появления первой работы Дж. Неймана и С. Улама в 1948 году по применению метода Моте-Карло, компьютерное моделирование четко разделилось на три направления, представленные в классификации.

М2-1 – метод Монте-Карло или численное моделирование (иногда еще по-старинке называемый методом статистических испытаний) использует методы М1-2, а ВЭ состоит в численном решении математических уравнений при заданных значениях параметров и начальных условий. Этим методом можно с большим успехом вычислять любые неберущиеся аналитически многократные интегралы, решать системы алгебраических, дифференциальных и интегральных уравнений. В настоящем пособии метод Монте-Карло не рассматривается специально и читатель может обратиться к многочисленной литературе ему посвященной.

М2-2 – метод имитационного моделирования (simulation modeling) для которого характерно воспроизведение на ЭВМ процесса функционирования системы. При этом имитируется процесс проектирования или производства РЭС с сохранением его логической структуры и последовательности протекания во времени, что позволяет получить информацию о состоянии объекта в заданные моменты времени. Дальнейшее рассмотрение в главе 4 относится именно к этому методу моделирования.

М2-3 – вид компьютерного моделирования, позволяющего получить статистические данные об объекте, чаще всего с использованием метода планирования эксперимента [23]. Кроме того, можно назвать две хорошие монографии: Кляйнен Дж. «Статистические методы в имитационном моделировании» и Афифи А., Эйзен С. «Статистический анализ. Подход с использованием ЭВМ». В настоящее время существует большое число ППП, которые можно условно разбить на три группы:

• пакеты углубленного статистического анализа для специалистов по математической статистике с собственным языком, позволяющим программировать новые статистические процедуры (Systat, SAS, Statgraphics)

• пакеты базовой статистики, ориентированные на пользователей, не являющихся специалистами по статистическому анализу и содержащие классические методы анализа с дружественным пользовательским интерфейсом в виде многочисленных пояснений и подсказок (разделы MatLab, MiniTab, Статистика).

• проблемно-ориентированные пакеты, использующие терминологию и критерии в исследуемой конкретной предметной области.

Рассмотрим достоинства компьютерного моделирования:

1. Возможность объединения традиционных математических методов и экспериментальных машинных методов.

2. Высокая эффективность применения для исследования АСНИ, САПР, экспертных систем. По данным RAND Corp. консалтинговые фирмы из всей гаммы возможных средств анализа – линейное, нелинейное, динамическое программирование, методы исследования операций, имитационное моделирование более чем в 60% случаев прибегают к помощи ИМ.

3. Возможность исследования объектов, физическое моделирование которых экономически не оправдано или неосуществимо.

4. Испытание объекта связано с опасностью для здоровья человека.

5. Исследование еще не существующих объектов.

6. Исследование труднодоступных или ненаблюдаемых объектов.

7. Исследование экологических, социальных или экономических систем .

8. Исследование объектов практически любой сложности при снятии ограничения на вид законов распределения случайных величин.

Естественно, что при большом числе достоинств ИМ не может не обладать рядом недостатков, в их числе дороговизна (время и деньги), меньшая степень общности по сравнению с аналитическим моделированием и отсутствие, в настоящее время, методов оценки адекватности ИМ.

В дальнейшем будем рассматривать только особенности имитационного моделирования (ИМ).

Процесс ИМ системы S можно разделить на три последовательно выполняемых этапа (рис. 3.2):

Э1. Построение математической (концептуальной) модели S` см. раздел 3.2.

Э2. Разработка моделирующего алгоритма S`` см. раздел 3.3.

Э3. Исследование системы S с помощью модели S`` см. главу 4.

Э1 Э2 Э3

S S` S``

Рис. 3.2 Этапы представления модели

Процесс ИМ не является строго поступательным, между этапами существуют обратные связи, позволяющие вводить новую информацию, вносить уточнения и корректировки.