
- •Тема 1: Техника первичных измерительных преобразователей (датчиков).
- •Техника первичных преобразователей
- •Тема:2 Характеристики функциональных звенеьев измерительного канала
- •Цифровые преобразователи
- •Преобразователи кода в напряжение – пкн
- •Аналого-цифровые преобразователи.
- •Пнк поразрядного сравнения
- •Погрешности цифрового преобразования
- •Восстановление аналоговых сигналов (аналоговый вывод )
- •Тема 3:Взаимосвязь структуры аппаратных и программных средств иис
- •Характеристика операционных систем реального времени - ос рв
- •Типы усд.
- •Тема 4: Расчёты параметров иис. Выбор масштаба, калибровка звеньев усд.
- •Информационный расчёт иис (Выбор частоты опроса датчика в ик).
- •Рассмотрим в выражении для составляющую ошибки квантования – .
- •Рассмотрим в выражении для составляющую ошибки дискретизации –
- •Оценка относительной погрешности дискретизации
- •Тема 5: Сжатие измерительной информации
- •Математические аспекты сжатия информации Элементы теории кодирования
- •Адаптивная дискретизация измеряемого сигнала
- •Апертурные алгоритмы сжатия данных
- •Элементы теории интерполяции, экстраполяции и сглаживания
- •Апертурные алгоритмы на базе полиномиальной интерполяции
- •Обоснование алгоритма адаптивной линейной интерполяции
- •Апертурные алгоритмы, использующие экстраполяцию
- •Сглаживание
- •Цифровая фильтрация первого порядка
- •Оптимальная фильтрация
- •Тема 6: микропроцессорные средства сбора и первичной обработки информации
- •6.1. Характеристика и признаки классификации средств сбора и первичной обработки информации
- •6.2. Основные типы измерительных микропроцессорных средств (имс)
- •Примеры реализации имс на основе приведенной классификации
- •6.3.1. Интегральные средства сбора, измерения и преобразования сигналов
- •6.3.2. Микропроцессорные цифровые измерительные приборы.
- •6.3.3. Микроконтроллерные проблемно-ориентированные подсистемы и устройства (логгеры).
- •6.3.4. Микропроцессорные подсистемы сбора, измерения и обработки данных
- •3.8. Открытые магистрально-модульные многопроцессорные имс.
- •Scada – средства автоматизированного проектирования срв.
Сглаживание
Если на сигнал наложена помеха (высокочастотная), то применение лишь интерполяции не обеспечит эффективного сжатия информации. В ряде случаев более эффективным может оказаться сглаживание (фильтрация) с последующей интерполяцией. Сглаживание, естественно, может быть реализовано лишь тогда, когда полезный сигнал и сигнал помехи имеют некоторые различные свойства. Рассмотрим несколько примеров эффективного сглаживания сигналов, использующих обработку сигнала с помощью ЭВМ:
1) Цифровая фильтрация - чаще всего первого порядка или оптимальная фильтрация;
2) Сглаживание измеренных значений за счет формирования средних -метод скользящего среднего или прогрессивная интерполяция;
3) Фильтрация сигналов с помощью фильтра нижних частот (ФНЧ)).
Цифровая фильтрация первого порядка
В качестве фильтра нижних частот используется звено задержки первого порядка с временной константой Т, удовлетворяющее дифференциальному уравнению:
![]()
где ![]() - фильтруемая входная величина,
- фильтруемая входная величина,
![]() - отфильтрованная выходная величина.
- отфильтрованная выходная величина.
При
цифровой фильтрации ЭВМ по программе
выполняет функцию фильтра. ЭВМ работает
как дискретная система: изменяемые во
времени значения
![]() и
и
![]() доступны только в моменты времени tk-1,
tk,
tk+1,
... .
Дифференциальное уравнение преобразуется
в следующее разностное уравнение:
доступны только в моменты времени tk-1,
tk,
tk+1,
... .
Дифференциальное уравнение преобразуется
в следующее разностное уравнение:
![]()
где ![]() - значение выборки сигнала в момент
времени
- значение выборки сигнала в момент
времени
![]() .
.
После решения относительно отфильтрованной выходной величины:
![]()
где ![]() - интервал дискретизации сигнала.
- интервал дискретизации сигнала.
Такую рекурсивную форму можно использовать в качестве алгоритма работы ЭВМ:
![]()
где ![]() - выбираемый фактор сглаживания, 0<А<1.
- выбираемый фактор сглаживания, 0<А<1.
Таким образом, работа фильтра заключается в получении отфильтрованных значений сигнала из текущего зашумленного с учетом предыдущего значения. А - постоянный коэффициент, принимающий значения 1>A³0,5 для более динамичных сигналов, передаваемых в условиях слабых помех, 0,5>A>1 -наоборот, для медленно изменяющихся сигналов на фоне сильных помех.
Оптимальная фильтрация
Методы теории оптимальных фильтров основываются на методах математической статистики. Оптимальный фильтр - это передаточная система, выполняющая оптимальную фильтрацию сигнала помехи. В качестве критерия оптимизации выступает минимум величины среднеквадратической погрешности. Можно использовать и другие критерии оптимизации, в зависимости от того, какой аспект использования выдвигается на передний план. В методе оптимальной фильтрации, как и в методе цифровой фильтрации первого порядка, используют для получения текущего отфильтрованного значения сигнала предыдущее отфильтрованное. Он дает взвешенные средние значения в виде:
![]()
где ![]() - весовая показательная функция, n
- весовой
показатель.
- весовая показательная функция, n
- весовой
показатель.
Такую рекурсивную формулу удобно применять в качестве алгоритма на ЭВМ. В качестве фактора сглаживания выбирается весовой показатель n. Очевидно, что при n=1 получаем среднее арифметическое значение предыдущего отфильтрованного значения сигнала и текущего зашумленного. Именно это значение берется в качестве текущего отфильтрованного значения сигнала. Таким образом, при n>1 будем получать соответствующие моменты более высокого порядка, причем при увеличении n влияние предыдущего отфильтрованного значения сигнала каждый раз значительно увеличивается.
Достоинством оптимальных фильтров является относительно небольшое количество вычислительных операций и, соответственно, простота реализации. Кроме этого, важным является то, что оптимальный фильтр используется в тех случаях, когда спектр частот полезного и налагаемого шумового сигналов находится в одной области значений, а их разделение традиционными ФНЧ или полосовыми фильтрами невозможно. Поэтому методы оптимальной фильтрации выполняют функцию выделения полезного сигнала на основе методов статистических оценок. Таким образом, данный метод может быть применен для высокодинамичных сигналов.
Прогрессивная интерполяция (метод усреднения)
Данный метод является простейшим методом повышения представительности измеренных значений за счет сглаживания случайных выбросов сигнала. Он используется главным образом в тех случаях, когда данные процесса служат для его контроля. Среднее значение формируется на основе измеренных значений по N циклам считывания:
![]()
Отдельные
значения S
суммируются. После выполнения суммирования
вычисляется среднее значение путем
деления суммы на число N.
Шум, в данном случае, рассматривается
в виде стационарного некоррелируемого
процесса и характеризуется значением
математического ожидания E(n),
которое при достаточном числе проб
стремится к нулю E(n)=0.
Среднее арифметическое из суммы выборок
сигнала с наложенным на него шумом будет
равно:![]()
![]() ,
,
где N - количество выборок в группе,
i - номер отсчета сигнала,
k - текущая выборка.
N
должно выбираться не более необходимого
для нахождения отсчета сигнала. Можно
записать: ![]() .
.
Если
частота выборок сигнала превышает
высшую частоту спектра сигнала
![]() , то
, то
![]() , откуда
, откуда
![]() .
.
Поскольку
среднее значение шума равно нулю, то
значит в пределе при достаточно большом
N
мы должны получить в результате
суммирования значение сигнала без
примеси шума. Так как E(n)=0,
доля примеси шума зависит от величины
его дисперсии. Учитывая, что дисперсия
![]() случайной величины x
равна
случайной величины x
равна
![]() запишем:
запишем:

Если
считать, что выборки не коррелируют
друг с другом, можно окончательно
записать, т.к.
![]() :
:
![]()
Это
означает, что при усреднении N выборок
сигнала и шума ожидаемое среднее значение
амплитуды соответствует амплитуде
сигнала, а дисперсия составляет
![]() .
Поскольку среднее значение шума равно
нулю, тогда для усредненного сигнала
по N
выборкам каждый отсчет
.
Поскольку среднее значение шума равно
нулю, тогда для усредненного сигнала
по N
выборкам каждый отсчет
 .
.
.
Отсюда
следует, что
отношение сигнал/шум должно расти при
усреднении пропорционально значению
![]() .
.
Несмотря на кажущуюся сложность реализации прогрессивной интерполяции (необходимость использования интегратора или сумматора, усредняющего устройства и интерполятора), а также существенное запаздывание, подобный метод сглаживания в системах уплотнения информации имеет ряд преимуществ перед запаздывающей фильтрацией, особенно в тех случаях, когда передаточная функция оптимального фильтра имеет высокий порядок. В подобной ситуации осуществить оптимальный фильтр бывает довольно сложно, и к тому же возникает проблема обеспечения устойчивости системы в целом.
Применение данного метода сглаживания помех имеет и ряд существенных ограничений:
Во-первых, как и метод цифровой фильтрации, метод усреднения эффективно применим для сигналов с низкой динамикой изменения и с высокочастотным сигналом помехи.
Во-вторых, данный метод характеризуется относительно большими временными затратами, т.к. при увеличении числа N, значительно увеличивается временная задержка формирования результирующих значений и резко возрастают требования к быстродействию аппаратуры сбора данных. Поэтому в случае быстроизменяющихся процессов, в которых вслед за сбором данных должны выполняться расчеты и выдаваться управляющие сигналы, метод прогрессивной интерполяции мало пригоден.
Широкое распространение на практике находит алгоритм «скользящего среднего», в котором также используется усреднение. В данном алгоритме с приходом каждой новой выборки усредняются последние N зашумленных выборок, а в канал передается поток отфильтрованных выборок, следующих с той же частотой, что и исходные. Не уступая в качестве сглаживания алгоритму прогрессивной интерполяции, алгоритм «скользящего среднего», может применяться для сглаживания более динамичных сигналов
Фильтрация сигналов с помощью фильтра нижних частот (ФНЧ)
Предположим,
что на входе идеального ФНЧ действует
смесь сигнала
![]() со спектральной плотностью
со спектральной плотностью
![]() и помехи
и помехи
![]() со спектральной плотностью
со спектральной плотностью
![]() и что сигнал и помеха статистически
независимы. Обычно полезный сигнал
менее широкополосен и его спектр падает
с ростом w.
Очевидно, в этом случае существует
некоторое оптимальное значение полосы
пропускания фильтра -
и что сигнал и помеха статистически
независимы. Обычно полезный сигнал
менее широкополосен и его спектр падает
с ростом w.
Очевидно, в этом случае существует
некоторое оптимальное значение полосы
пропускания фильтра -
![]() , которое минимизирует среднеквадратическую
погрешность фильтрации, поскольку
увеличение полосы пропускания будет
приводить к уменьшению погрешности
, которое минимизирует среднеквадратическую
погрешность фильтрации, поскольку
увеличение полосы пропускания будет
приводить к уменьшению погрешности
![]() от срезания высокочастотных составляющих
спектра сигнала
от срезания высокочастотных составляющих
спектра сигнала
![]() ,
но будет увеличивать погрешность
,
но будет увеличивать погрешность
![]() от действия помехи
от действия помехи
![]() Суммарное значение погрешности
фильтрации, если пренебречь запаздыванием
ФНЧ, можно записать в виде:
Суммарное значение погрешности
фильтрации, если пренебречь запаздыванием
ФНЧ, можно записать в виде:

Оптимальное
значение
![]() можно найти из соотношения:
можно найти из соотношения: ![]() .
.
Например,
для телеграфного сигнала с экспоненциальной
корреляционной функцией
![]() ,
на который накладывается белый шум,
wопт
можно найти
следующим образом. Пусть
,
на который накладывается белый шум,
wопт
можно найти
следующим образом. Пусть
![]() ,
,
![]() , так как
, так как
![]()
![]()
Учитывая
что
![]() ;
;![]() ;
;![]()
![]() ,тогда
,тогда
![]()
![]()
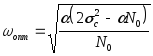
П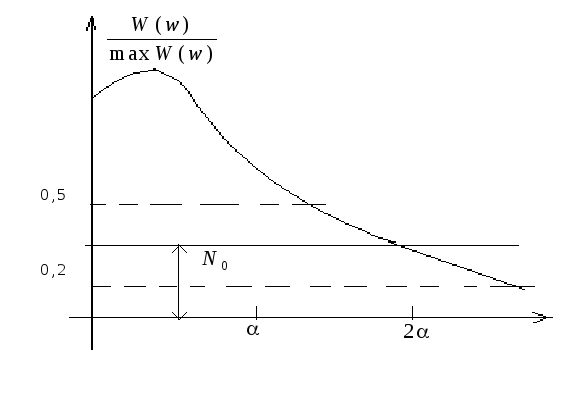 одбирая
параметры фильтра (параметрическая
оптимизация), можно добиться весьма
эффективного сглаживания сигнала. Как
уже было показано выше качество
интерполяции с помощью хорошо настроенного
ФНЧ выше , чем у интерполятора первого
порядка.
одбирая
параметры фильтра (параметрическая
оптимизация), можно добиться весьма
эффективного сглаживания сигнала. Как
уже было показано выше качество
интерполяции с помощью хорошо настроенного
ФНЧ выше , чем у интерполятора первого
порядка.
