Рассмотрим в выражении для составляющую ошибки квантования – .

При равномерном квантовании шаг квантования – постоянный. Если процесс стационарный, то шкала (динамический диапазон сигнала) для всех выборок одинакова, поэтому число уровней квантования не зависит от номера выборки: , где – число разрядов бинарного кода .

Погрешность квантования является случайной функцией времени, вероятностные характеристики которых зависят от вероятностных характеристик процесса. В этом смысле погрешность квантования можно рассматривать как внешнюю аддитивную помеху (шум квантования). При малой допустимой погрешности квантования, когда шум квантования в различных выборках можно считать коррелированным, при этом можно ограничиться оценкой его одномерных вероятностных характеристик. Если началу шкалы соответствует уровень с номером , а концу шкалы уровень и значение выборки отождествляется с ближайшим уровнем квантования или с серединой между соседними уровнями, то максимальная по модулю погрешность квантования:

; .

При , как это обычно бывает на практике изменением плотности вероятности значений выборки на интервале, равном шагу квантования можно пренебречь и считать, что она распределена равномерно.

Тогда



Откуда, считая сигнал нормально распределённым т.е.

 (при равномерном распределении )

Откуда 

Найдём , по определению: ,

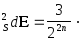
что и требовалось доказать.

Рассмотрим в выражении для составляющую ошибки дискретизации –

Рассматриваем как и в предыдущем случае пример равномерной дискретизации () стационарного процесса с известной корреляционной функцией . В качестве аппроксимирующей функции примем полином нулевой степени (ступенчатая интерполяция), при которой: , .

В момент времени текущая ошибка дискретизации равна:

; (1)

Дисперсия погрешности дискретизации при ступенчатой интерполяции выражается равенством . Раскрывая скобки и

учитывая, что у случайного стационарного эргодического процесса для случайной величины :





имеем:

,

где – математическое ожидание , – корреляционная функция для .

Исходя из этого запишем формулу для в следующем виде:

откуда из (1) и учитывая, что

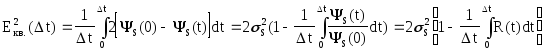
,где - удельная корреляционная функция. Что и требовалось доказать.

Выражения для ошибок дискретизации и квантования для линейной интерполяции и критерия максимального отклонения, приведенные в таблице 1 здесь не доказываются, но при их определении используют подходы, аналогичные рассмотренным выше.

Оценка относительной погрешности дискретизации

Для сигналов с ограниченным спектром частот (), когда квантование переменной производится с постоянным шагом - Т для формулы Лагранжа представляет интерес оценка относительной погрешности интерполирования.

При интерполировании по формуле нулевого порядка, когда выходной сигнал представляет собой ступенчатую функцию, относительная погрешность дискретизации.

1) , где - интервал дискретизации, - граничная частота

В случае интерполяции по формуле первого порядка (Выходной сигнал: кусочно-линейная функция)

2)

Для формулы второго порядка

3)

Из этих формул можно определить параметры построения интерполяционного у-ва , добиваясь чтобы разрядность кодера выбиралась . В общем виде выражение для относительной погрешности можно записать: , где к - степень интерполирующего полинома.

На практике чаще всего в качестве интерполятора используется фильтр нижних частот (ФНЧ). Представляет интерес сравнить погрешность ФНЧ с погрешностями для интерполятора, построенного на базе полинома Лагранжа. Поэтому, опуская доказательство выражений, приведенных выше для -1), 2), 3), покажем как определить в случае применения ФНЧ. Рассмотрим пример, когда на вход ФНЧ подается последовательность выборок, амплитуда которых изменяется по синусоидальному закону. Блок-схема преобразователя, временные и спектральные характеристики сигналов приведены ниже.

ФНЧ можно рассматривать как некоторое звено задержки . При считывании сигналов, соответствующих не максимально возможным значениям спектральных составляющих-, а выбранным граничным значениям , появляются ошибки, определяемые разностью амплитуд выходных сигналов и входных сигналов элемента опроса. Приведенные к амплитуде входного сигнала они запишутся:

Амплитуда и фаза выходного сигнала ФНЧ (с идеальной прямоугольной характеристикой- звена задержки) получается на основе известной частотной зависимости для спектра импульса с амплитудой :

Ошибку как функцию периода опроса - Т и максимальной частоты -частота среза ФНЧ) можно оценить по величине амплитуд опрашивающего звена и звена задержки - ФНЧ. При синусоидальной форме входного сигнала S(t) в выходном учитываем только одну главную гармонику. В этом случае амплитуда соответствует модулю указанной выше частоты зависимости частот и приведенной погрешности. Погрешность преобразования можно записать:

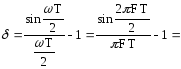(подставляем граничную частоту спектра для общего случая)

Используем запись и при незначительной ошибке ограничимся первыми двумя членами.

Сравнивая полученный результат с записанными ранее для интерполятора, видим что качество интерполяции с помощью хорошо настроенного ФНЧ лежит между интерполятором 1-го и 2-го порядков.

Зависимость частоты от допустимой ошибки опроса:

	0,000001	0,00001	0,0001	0,001	0,01	0,1
1/FT	1280	410	128	41	12,8	4,1

При допустимой ошибке частота опроса выбирается примерно в 100 раз больше граничной частоты спектра сигнала, а при 1%() лишь в 10 раз больше. К примеру ступенчатая интерполяция при допустимой ошибке 1% имеет коэффициент увеличения граничной частоты спектра к=314, линейная- к=22, второго порядка- к=12.

Мы рассмотрим пример идеального ФНЧ. Для реальных фильтров, например широко применяемый в технике фильтр Баттеворта по эффективности приближается к линейной интерполяции, особенно с ростом порядка фильтра.

Фильтр Баттеворта имеет амплитудно-частотную характеристику:

, где к(j)- комплексный коэффициент передачи фильтра.

m- порядок фильтра m=1,2,3...

- соответствует уровню половинной мощности на амплитудно-частотной характеристике фильтра =

Получение оценки величины означает, что при высокой требуемой точности восстановления аналогового сигнала шаг дискретизации должен назначаться значительно меньше интервала корреляции . Это означает сильную коррелированность отсчетов, приводящую к избыточности объема сообщения. В полученной оценке не учтена задержка сообщения, необходимая для построения полинома. Учет задержки приведет к росту погрешности, что важно для различного рода следящих систем, в таких системах лучше применять полиномы 0-го порядка или переходить к экстраполяционным методам восстановления сигнала.

- относительный квадрат ошибки восстановления.

На практике пользуются в зависимости от типа интерполятора и допустимой ошибки специальными коэффициентами зависимости от этой ошибки определяющими частоту дискретизации путем умножения граничной частоты спектра сигнала или частоты Котельникова на такой коэффициент.

Сопоставление критериев выбора времени цикла считывания для практических случаев

(когда неизвестны характеристики сигнала, но известны параметры звеньев по которым они передаются, частота опроса -)

Класс процесса	Время цикла Т	Примечание
Известны динамические характеристики процесса
Любой а) не задан вид корреляционной ф-ии б) не оценив погрешность восстановления в) не определен тип интерполятора при восстановлении сигнала	или (обычно к=510)	Граничная частота - выбирается так, чтобы соотношение амплитуд составляло , где G(f) - амплитудно-частотная характеристика (АЧХ) к - коэффициент увеличения частоты Котельникова, зависящий от необходимой точности восстановления процесса. - соответствует уровню половинной мощности на АЧХ. При восстановлении полиномом Лагранжа коэффициент к можно определить из соотношений: ,где - приведенная максимальная погрешность, n=0,1,2... - степень интерполируемого полинома. При восстановлении с помощью ФНЧ(в качестве интерполятора) или ,где - относительный квадрат ошибки восстановления, m=1,2,3... порядок фильтра при m=1 , когда ампл. спектр сигнала по мощности совпадает с х-кой фильтра.
Когда известны частотные или временные характеристики звеньев, через которые передается сигнал
Периодический с доминирующим временем запаздывания		Инерциальная система с временем запаздывания -
Х-ка с преобладанием низких частот		- время успокоения, в течение которого процесс остается в пределах границ конечного значения передаточной функции
Гармонический с частотой синусоиды		Узкополосная система на определенной частоте F - частота синусоиды