
- •Неопределённый интеграл
- •Интегрирование подстановкой
- •Определённый интеграл приложения определённого интеграла
- •Комплексные числа
- •Упражнения
- •Алгоритм перевод комплексного числа из алгебраической в тригонометрическую форму.
- •II. Комплексно-сопряженные числа.
- •III. Действия с комплексными числами в алгебраической форме.
- •IV. Действия с комплексными числами в тригонометрической форме.
- •V. Решение квадратных уравнений.
- •Модуль числа.
IV. Действия с комплексными числами в тригонометрической форме.
При умножении комплексных чисел их модули перемножаются, а аргументы складываются:
z1z2= r1 r2 ( cos (φ1 + φ2) + i (sin (φ1 + φ2))
При делении комплексных чисел их модули делятся, а аргументы вычитаются:
![]() (
cos (φ1
- φ2)
+ i (sin (φ1 - φ2)).
(
cos (φ1
- φ2)
+ i (sin (φ1 - φ2)).
Формула Муавра.
zn= (r ( cos φ+ i sin φ))n= rn( cos nφ + i sin nφ),
Пример:
Частное
![]() комплексных
чисел
комплексных
чисел
![]() и
и
![]() равно …
равно …
Решение:
Воспользуемся
формулой:
 Получим:
Получим:

Ответ:
![]()
2.
Степень комплексного числа
![]() равна …
равна …
Решение:
Согласно
формуле Муавра
![]() находим:
находим:
![]()
Ответ:
![]()
Решите самостоятельно:
1.
Произведение комплексных чисел
![]() и
и
![]() равно …
равно …
Ответ:
![]()
2.
Произведение комплексных чисел
 и
и
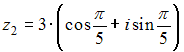 равно …
равно …
Ответ:

4.
Дано комплексное число
![]() .
Тогда значение
.
Тогда значение
![]() равно …
равно …
Ответ:
![]()
V. Решение квадратных уравнений.
Любое уравнение n-ой степени на множестве комплексных чисел имеет ровно n корней, причём корни считаются столько раз, какова их кратность в данном уравнении.
Уравнения вида az2 + bz + c = 0 (где z- комплексное число) решаются по общей формуле:
z1,2=![]() ,
где
,
где
![]() ,при
этом:
,при
этом:
если D=0, уравнение имеет один действительный корень,
если D>0, уравнение имеет два действительных корня,
если D<0, уравнение имеет два мнимых корня.
Пример:
Корни
квадратного уравнения
![]() равны …
равны …
Решение:
Учитывая
равенство
![]() мы
можем найти корни данного уравнения,
принадлежащие множеству комплексных
чисел; получим:
мы
можем найти корни данного уравнения,
принадлежащие множеству комплексных
чисел; получим:
![]()
![]()
![]()
![]()
![]() Корнями
уравнения являются комплексные числа
Корнями
уравнения являются комплексные числа
![]() и
и
![]()
Решите самостоятельно:
-
Корни квадратного уравнения
 равны …
равны …
Ответ:
![]()
![]()
-
Корни квадратного уравнения
 равны …
равны …
Ответ:
Корнями
уравнения являются комплексные числа
![]() и
и
![]() .
.
-
Корни квадратного уравнения
 равны …
равны …
Ответ:
![]()
![]()
-
Корни квадратного уравнения
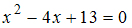 равны …
равны …
Ответ:
![]()
![]()
-
Модуль числа.
Определение:
Модулем
комплексного
числа z
= a
+ bi
называется число![]() и
обозначается
и
обозначается
![]() ,
т.е.
,
т.е.
![]() .
.
Пример:
Модуль
комплексного числа
![]() равен …
равен …
Решение:
Модуль
комплексного числа вычисляется по
формуле
![]() ,
где
,
где
![]() –
действительная, а
–
действительная, а
![]() –
мнимая часть комплексного числа. Тогда
–
мнимая часть комплексного числа. Тогда
![]()
Ответ:
![]()
Решите самостоятельно:
1.
Модуль
комплексного числа
![]() равен …
равен …
Ответ:
![]()
2.
Модуль комплексного числа
![]() равен …
равен …
Ответ:
![]()
3.
Модуль комплексного числа
![]() равен …
равен …
Ответ:
![]()
Р Я Д Ы
Ч
Ответа нет
 исловые
ряды:
исловые
ряды:
1
Ответ ряд расходится![]()
нет
2.Достаточные условия:
P>1
– ряд расходится
I
P<1 –
ряд сходится
 .Признак
Даламбера:
.Признак
Даламбера: ![]()
P=1 – нет
ответа
II.Признак сравнения:
1)![]() – сходится
– сходится ![]() -
сходится, т.к. сходится его мажорантный
ряд
-
сходится, т.к. сходится его мажорантный
ряд
2)![]() – расходится,
– расходится, ![]() -
расходится как мажорантный для
расходящегося
-
расходится как мажорантный для
расходящегося
III.Эталонные ряды(г.п.):
![]() -сходится
|q|<1,
-сходится
|q|<1,
![]()
![]() – расходится
т.к. гармонический
– расходится
т.к. гармонический
![]() ,
,![]()
IV. Знакопеременные ряды:
![]() – ряд модулей
– ряд модулей
![]() ,
сходится
,
сходится
![]() -абсолютно
сходящийся
-абсолютно
сходящийся
расходится - ответа нет
V. Знакочередующиеся ряды
 по
признаку Лейбница
по
признаку Лейбница
 – сходится
– сходится
Функциональные
ряды:
![]()
1.Степенные:
![]() (по степеням x)
(по степеням x)
![]() (по степеням
(по степеням ![]() ).Область
сходимости – множество всех точек
сходимости.
).Область
сходимости – множество всех точек
сходимости.
2.Ряд Тейлора – Маклорена:
![]()
![]()
![]() R
сходимости =
R
сходимости = ![]()
![]()
![]()
![]() интервал
(-R;R)
интервал
(-R;R)
3.Тригонометрические ряды. Ряды Фурье.
опр:![]() ;
слагаемое – гармоники,
;
слагаемое – гармоники, ![]() - амплитуды, 1,2,n-частоты
- амплитуды, 1,2,n-частоты
П ри
ри
![]()
![]()
![]() Коэффициенты Фурье
Коэффициенты Фурье
![]()
![]() -частоты
-частоты
![]()
![]()
![]()
Е сли
функция чётная
сли
функция чётная ![]()
Е сли
разложить по cos чётным образом
продолжить график
сли
разложить по cos чётным образом
продолжить график
Е сли
функция нечётная
сли
функция нечётная ![]()
Е сли
разложить по sin нечётным образом
продолжить
сли
разложить по sin нечётным образом
продолжить
|
СУММА ЧИСЛОВОГО РЯДА |
1.Дан
числовой ряд
 .
Частичная сумма
.
Частичная сумма
![]() равна …
равна …

4.Дан
числовой ряд:
 Его
частичная сумма
Его
частичная сумма
![]() равна …
равна …
![]()
ТЕМА ЧИСЛОВЫЕ РЯДЫ.
|
……… и
их четвертыми членами.
|
…………и
их пятыми членами.
|
||||||||||||||||||||||||
|
……….их
четвертыми членами.
1.
|
их пятыми членами.
.
|
Для
исследования вопроса о сходимости
числового ряда
![]() используется
необходимый признак сходимости числового
ряда
используется
необходимый признак сходимости числового
ряда
![]() Тогда
могут сходиться ряды …
Тогда
могут сходиться ряды …
1.
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
Решение
1)
 .
Тогда
.
Тогда
 .
Достаточный признак сходимости
выполняется, значит, данный ряд может
сходиться.
2)
.
Достаточный признак сходимости
выполняется, значит, данный ряд может
сходиться.
2)
 .
сходиться.(предел равен нулю т.к в
знаменателе N
в большей степени)
3)
.
сходиться.(предел равен нулю т.к в
знаменателе N
в большей степени)
3)
![]() .
.
 .
расходится.
4)
.
расходится.
4)
 .
.
 .
расходится.
.
расходится.
2.
|
|
|
|
3. ПРИМЕРЫ РЯДОВ
|
сходятся |
сходятся |
расходятся |
расходятся |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
ТЕМА ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ РЯДОВ. |
|||||
Для
исследования числового ряда
![]() на
сходимость можно пользоваться признаком
Даламбера
на
сходимость можно пользоваться признаком
Даламбера![]()
 и признаком Коши
и признаком Коши
![]() Тогда
сходящимися являются ряды …
Тогда
сходящимися являются ряды …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
1)
Для ряда
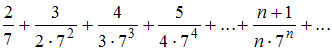 воспользуемся
признаком Даламбера.
воспользуемся
признаком Даламбера.
 Тогда
получим:
Тогда
получим:

 Так
как
Так
как
![]() ,
то данный ряд сходится.
2) Для ряда
,
то данный ряд сходится.
2) Для ряда
 воспользуемся
признаком Даламбера.
Имеем:
воспользуемся
признаком Даламбера.
Имеем:
 тогда
получим:
тогда
получим:
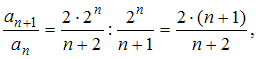
 .
Так
как
.
Так
как
![]() ,
то данный ряд расходится.
3) Для ряда
,
то данный ряд расходится.
3) Для ряда
 воспользуемся
признаком Коши.
Имеем:
воспользуемся
признаком Коши.
Имеем:
 тогда
получим:
тогда
получим:

 Так
как
Так
как
![]() ,
то данный ряд сходится.
4) Для ряда
,
то данный ряд сходится.
4) Для ряда
 воспользуемся
признаком Коши.
Имеем:
воспользуемся
признаком Коши.
Имеем:
 тогда
получим:
тогда
получим:
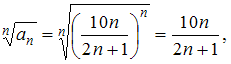
 Так
как
Так
как
![]() ,
то данный ряд расходится.
,
то данный ряд расходится.
2.![]() исследования числового ряда
исследования числового ряда
![]() на
сходимость можно пользоваться признаком
Даламбера
на
сходимость можно пользоваться признаком
Даламбера![]()
 и признаком Коши
и признаком Коши
![]() Тогда
сходящимися являются ряды …
Тогда
сходящимися являются ряды …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
1)
Для ряда
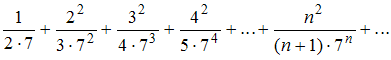 воспользуемся
признаком Даламбера.
воспользуемся
признаком Даламбера.
 Получим
Получим
 Тогда
Тогда
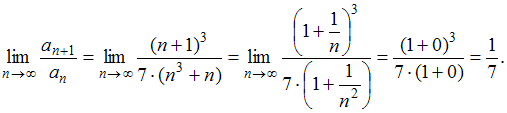 Так
как
Так
как
![]() ,
то данный ряд сходится.
2) Для ряда
,
то данный ряд сходится.
2) Для ряда
 признак
Даламбера.
признак
Даламбера.
 Получим
Получим
 Тогда
Тогда
 расходится.
3)
Для ряда
расходится.
3)
Для ряда
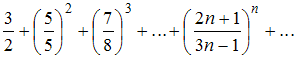 признаком
Коши.
признаком
Коши.
 Получим
Получим


![]() ,
ряд сходится.
4) Для ряда
,
ряд сходится.
4) Для ряда
 признак Коши.
признак Коши.
 Получим
Получим
 Тогда
Тогда
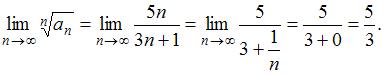
![]() ряд расходится.
ряд расходится.
3.
|
Сходятся по Деламберу |
Расходятся по Деламберу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сходятся по Коши |
Расходятся по Коши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Для
степенного ряда
![]() радиус
сходимости R
равен …1
радиус
сходимости R
равен …1
|
Радиус
сходимости R
степенного ряда
|
|
|
|
Для
степенного ряда
|
|
|
|
|
|
|
|
Радиус сходимости
R
степенного ряда
|
|
Решение:
Радиус
сходимости степенного ряда
 находится
по формуле
находится
по формуле
 По
условию задачи имеем, что
По
условию задачи имеем, что

 примеры
примеры
1.Известно,
что ряд Маклорена для функции
![]() имеет
вид
имеет
вид
 Тогда
Тогда
![]() равняется
…
равняется
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Напоминаем,
что нужно сделать подстановку – вместо
x
записать
![]() Получим
Получим

2.Известно,
что ряд Маклорена для функции
![]() имеет
вид
имеет
вид
 Тогда
Тогда
![]() равняется …
равняется …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Известно,
что ряд Маклорена для функции
![]() имеет
вид
имеет
вид
 Тогда
Тогда
 …
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Известно,
что ряд Маклорена для функции
![]() имеет
вид
имеет
вид
 Тогда
Тогда
![]() равняется …
равняется …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Cделаем
подстановку, вместо x
запишем
![]() тогда
получим:
тогда
получим:

|
Тогда
|
|
||||
|
Тогда
|
|
||||
|
Тогда
|
|
||||
|
Тогда
|
|

 ,
2.
,
2.



 2.
2.





























 радиус
сходимости R равен …2
радиус
сходимости R равен …2 равен …10
равен …10







